서 론
기후변화 대응과 탄소중립이 중요한 정책과제로 대두하면서 에너지원을 친환경 재생에너지로 전환하는 것은 중요한 과제가 되었다. 산림 바이오매스의 에너지 이용은 탄소중립으로 평가하여 배출로 계산하지 않는데, 이는 나무가 자라면서 대기의 탄소를 흡수한 것이고 벌채에서 이미 배출로 계상하므로 이중계산하지 않는다는 점 때문이다(KOPFI, 2020). 산림 바이오매스는 발열량이 높고 비용이 낮아 경제적이며(Seok et al., 2008), 석탄, 난방유 등에 비해 CO2 배출량이 낮다(Austrian Energy Agency, 2007).
현재 우리나라에서 연간 수백만 톤의 미이용 목재가 버려진다. 숲가꾸기, 병해충 피해목 방제, 가지치기 등 숲을 관리하는 과정에서 나타나는 각종 부산물은 산불의 원인이 될 수 있으며, 방치하기보다 적절히 수집·이용하는 것이 산림생태계의 건강성을 위해서도 필요하다(Kang, 2020). 미이용 산림 부산물을 방치하거나 소각하기보다 파쇄 등 간단한 공정을 거쳐 목재칩으로 제조하여 연료로 활용한다면 생태적, 환경적, 경제적으로 유익한 점이 많을 것이다. 건조, 압축, 성형 등 특정 공정이 필요한 목재펠릿에 비해 목재칩은 벌채지와 집하장 등에서 이동식 파쇄기를 통해 생산할 수 있어 생산비용이 낮고 근거리 공급이 가능하다는 장점이 있다. 그러나 부피가 커서 저장공간이 따로 필요하기 때문에 가정용 난방보다 산업용 또는 열공급 사업용으로 더욱 적합하다. 유럽에서는 목재펠릿 보일러는 주로 가정용으로, 목재칩은 대용량 열공급 사업용으로 많이 사용한다. 이러한 특징에도 불구하고 산림 바이오매스의 에너지 이용을 둘러싼 논란과 갈등은 여전히 진행중이다.
목재펠릿과 목재칩 등 목질계 바이오매스는 연소하여 열 생산 또는 발전(發電)에 이용할 수 있다. 그러나 나무는 에너지 밀도가 낮기 때문에 에너지 생산에 다량의 연료를 요구한다. 특히 나무를 이용한 발전의 에너지 효율은 15~30% 정도이며, 열 생산의 에너지 효율 70~80%보다 낮다(Min et al., 2020). 발전소는 대개 규모가 크기 때문에 특히 많은 연료를 필요로 하므로 산림과 지역사회에 부정적 영향을 미칠 수 있다. 이 때문에 산림 바이오매스는 전력 생산보다 열 생산에 더 적합한 것으로 알려졌다. 목재를 열에너지로 이용하는 방식은 과거부터 이어져 온 방식이며, 농산촌 지역 에너지로 활용하는 데 적합하다. 또, 지역의 산림자원을 지역의 에너지로 이용하는 것은 에너지의 지산지소, 지역 임업의 실행으로 이어진다는 점에서 그 의의가 크다.
산림을 벌채하여 직접 에너지로 사용하는 것은 그다지 효율적이지 않다. 목재의 다단계 이용 원칙에 따라 물질이용을 우선하고 마지막에 에너지로 이용하는 것이 바람직하다. 그러나 우리나라 목재기업의 다수가 인천과 군산 등 서부 항구도시에 위치하여 산림이 많은 강원과 경북에서는 수송비용이 적지 않고 이는 탄소배출과 관계된다. 이러한 관점에서 목재가공업체와 거리가 먼 농산촌에서는 산림자원을 지산지소(地産地消) 에너지원으로 이용하면서 지속가능하고 순환하는 임업을 실현하는 접근으로서 소규모 열에너지(또는 열전병합) 이용에 주목할 필요가 있다.
산림청은 미이용 산림 바이오매스의 발전 이용을 촉진하면서도 한편으로 산림에너지자립마을 사업을 추진한다. 이는 농산촌에 소규모 에너지 시설을 지원하여 지역의 에너지 자립을 추구하는 것이다. 산림 바이오매스 에너지 이용의 여러 장점에도 불구하고 그동안 추진했던 관련 사업이 성공을 거두지 못하는 실정이다. 에너지 시설 운영 경험이 부족하였고 안정적으로 정착하기까지 적절히 지원하지 못하였기 때문이다.
특히 정책에서 경제적 인센티브를 통해 에너지원 이용을 지원하는 정책은 상대적으로 많지 않다. 우리나라 재생에너지 정책은 발전의 에너지원 믹스 전환에 초점을 두며 열 생산에는 크게 부족하다. 정부 지원이 보일러 등 시설에만 집중하기 때문에 연료단가로 인한 수지타산이 낮아 지속적으로 가동되지 못하였다. 재생에너지 공급인증서(REC; Renewable energy certificate)는 발전에만 적용되고 열 공급에는 적용되지 않는다. 산림 바이오매스의 에너지 이용을 확대하기 위해서 열 생산에도 그에 상응하는 보조금이 필요하다. 예를 들어 유럽은 재생에너지원 열이 화석연료로 생산한 열보다 낮은 가격을 유지하도록 지원하는 등 재생에너지 지원 정책을 열 공급에도 적용한다(Park, 2019; Min et al., 2020). 이를 위해서 산림 바이오매스 연료를 이용하여 생산한 열에 지급하는 적정 보조금 수준을 도출하는 것이 선행되어야 한다.
산림 바이오매스의 에너지 이용에 관심이 높아지면서 관련 연구가 활발히 수행되었다. Seok et al.(2005)는 화석연료와 목질 바이오매스 연료의 단위 열량 생산비용을 비교했을 때, 목재칩보일러는 연탄보일러보다 못하지만 등유보일러보다 비용 효율적이라 하였다. Ministry of Commerce, Industry and Energy(2007)는 대형 목재칩 열병합발전의 경제성을 분석하였는데, 목재칩 가격 30,565~56,124원/m3에서도 경제성을 획득하기 어렵다고 밝히고 적정한 발전차액지원이 필요하다고 하였다. Suh et al.(2012)은 대형 목재칩 열병합발전의 운영 사례를 분석하고 경제성 확보를 위한 목재칩 가격을 도출하였다. 가동율 62%, 목재칩 가격은 55,153원/톤, 전기 판매가격 138.2원/kWh, 열 판매가격은 80,830원/Gcal으로 산정할 경우 20년 운영에서 내부수익률은 6.34%, 투자회수 기간은 약 15년으로 평가되었다. 경제성을 확보할 수 있는 목재칩 가격은 64,000원/톤 이하라고 하였다. Yanagida et al.(2017)은 산림 바이오매스를 이용한 열전병합 사업의 성립조건을 분석하였다. 열전병합 사업은 발전만 하는 것보다 경제성을 높일 수 있으나 1,200 kW 정도의 소규모 플랜트의 경우 발전효율이 낮아 낮은 열 판매단가에서 채산성을 확보하기 어렵다. 경제성을 높이기 위해 안정적인 열 수요 확보가 필요하다고 하였다. Song and Aguilar(2016)는 산림 바이오매스 이용 효율을 측정하기 위해 단위당 순유효에너지를 에너지 전환경로(energy conversion pathways)별로 추정하였는데, 산림 바이오매스는 난방 이용이 전력생산보다 2배 이상의 순유효에너지를 산출하는 것으로 나타났다.
발전을 우선하는 대형 열병합 발전소는 대량의 연료를 낮은 가격에 요구하기 때문에 국내 임업에서 대응하기 쉽지 않다. 이러한 이유로 소규모 분산형 열공급 시설을 검토할 필요가 있다. Cho(2018)는 화천군 산림바이오매스센터의 운영실태를 조사하였는데 난방에 필요한 연료 요구량보다 2.3배 많은 연료를 사용하며 참여가구도 점점 줄고 있다고 지적하였다. 이와 함께 연료 비용을 낮추기 위해 산림 바이오매스 수집 방법의 효율화 방안을 제안하였다. Yoo et al.(2019)는 일본 사례와 비교하면서 산림탄소순환마을의 운영 개선 방안을 제안하였다.
이 연구의 목적은 산림 바이오매스를 이용한 소규모 분산형 에너지 시설의 경제성을 분석하는 데 있다. 본 연구는 사례로서 ‘산림에너지자립마을’ 사업을 분석하는데, 선택의 유연성을 고려한 콜옵션(Call option) 가격결정모형을 이용한다. 투자를 통한 수익 회수라기 보다는 시설의 지속적 운영을 가능하게 하는 조건을 검토하였다. 이를 바탕으로 에너지 시설의 지속가능한 운영을 위해 지급하는 적정 보조금 수준을 도출하였다.
실물옵션모형 분석은 순현재가치법보다 수리적으로 다소 복잡하며 시간이 이산환경일 경우와 연속환경일 경우에 따라 다른 분석 방법이 적용된다. 연속환경일 경우 확률 미분방정식에 의존하기 때문에 복잡한 도출과정과 수치 해석에 의존하게 된다. 이 연구에서는 시간 변화(t)를 연(year)으로 가정하고 이산환경 분석에 적용되는 이항옵션모형을 사용하였다. 이항옵션모형의 장점은 확률 미분방정식에 비해 수리적인 복잡성이 덜 하고, 결과를 직관적으로 해석할 수 있다는 것이다.
재료 및 연구방법
분석자료에는 산림에너지자립마을 사례를 활용하였다. 이는 농산촌 마을을 소비처로 하여 열을 공급하여 에너지 자립 시스템을 구축하려는 것이다. 2020년 강원도 원주시와 전북 완주군이 사업 대상으로 선정되었다. 주요 설비는 에너지 생산 설비(칩보일러 400 kW, 발전설비 70 kW), 연료공급 설비(목재칩 저장창고, 건조시설, 운송장비, 파쇄장비), 열공급 설비(열배관 2.5 kW, 열교환기 50개, 배전 및 사무실)로 구성된다. 사업비는 4,426백만 원(국비 50%, 지방비 50%)이지만, 분석에서 설계비, 인허가 비용 등은 제외하였다. Table 1은 분석에 이용한 산림에너지자립마을 시설의 개요이다. 400 kW의 칩보일러는, 농촌 가구의 평균 열 수요량을 4,069 kcal/ha라고 하면(RRI and KIER, 2018), 대략 80여 가구에 열을 공급할 수 있다. 시간당 연료(목재칩) 소비량은 칩보일러에서 0.17톤, 발전설비에서 0.11톤이다. 가동률을 70%로 가정하면 연간 목재칩 소비량은 칩보일러에서 1,055톤, 발전기에서 692톤으로 나타난다. 이 정도라면 웬만한 지자체의 산림사업으로도 확보할 수 있다.
Source: KFS(2020).
에너지 시설 가동에는 감가상각비, 유지·보수비, 보험료, 경상인건비 등 고정 비용이 소요된다. 감가상각비는 열병합 발전시설의 운전기간을 25년으로 설정하고 25년 후 잔존 자산가치 50%를 가정하여 설정하였다. Suh et al. (2012)는 대형 열병합 발전시설을 대상으로 하면서 운전기간 20년, 잔존 자산가치 0으로 설정하였지만, 이 연구는 소규모 시설을 대상으로 하므로 일부 보수하여 시설 수명을 연장하거나 잔존가치를 높일 수 있다고 보았다. 선행연구(Suh et al, 2012)와 화천 산림바이오매스센터의 사례를 참고하여 연간 유지·보수비는 투자비의 0.5%, 보험료는 투자비의 0.23%를 각각 적용하였다. 시설 운영의 인건비는 1인 연 2,000만 원으로 설정하였다.
열 판매가격은 지역 난방공사 열 요금 정보를 이용하였으며(Public Data Portal), 전기 판매가격은 전력거래소(EPSIS)의 신재생에너지 거래의 정산금액을 이용하였다. 연료에는 목재칩 이용을 가정하고 일반 연료용 목재칩 가격을 적용하였다. Eco Network(2018)에 의하면 국내산 연료용 목재칩은 톤당 8만~9만 원에 거래된다. KFS(2020)에 의하면 ‘입목매입→벌목→소운반→파쇄’까지 비용은 7만 2,000~7만 8,700원으로 산정된다. 여기에 기타 관리비용 등을 포함하여 목재칩 가격을 톤당 9만 5,000원으로 가정하였다. 물론 지형 조건과 작업 방식에 따라 달라질 수 있다. 목재펠릿을 연료로 사용할 경우 연료비용이 지나치게 높아 분석에서 다루지 않았다.
산림 바이오매스 이용이 확산되려면 지자체 입장에서 투자 가치를 인식해야 한다. 또, 시설 운영자 입장에서 적어도 비용 이상의 수익을 확보할 수 있어야 한다. 본 연구에서 투자 타당성을 평가하기 위해 순현재가치법과 실물옵션 모형을 적용하였다. 순현재가치법은 최초 투자 시기부터 사업의 종료시기까지 연도별 순편익의 흐름을 현재가치로 환산한 것으로 사업의 가치를 나타내는 척도로 널리 이용된다. 이는 식 1과 같이 산출된다(Oh and Cho, 2013).
여기서 t는 시간, i는 이자율을 의미하며, Bi와 Ct는 각각 시간 흐름에 따라 발생하는 편익과 비용을 의미한다. 이때 편익은 전기와 열 판매 수익 및 REC를 통해 획득한 추가수익을 의미하며, 비용은 시설 투자비용, 시설 가동을 위한 고정비용과 연료비용을 의미한다.
경제성 평가는 특정 사업에서 발생하는 비용과 편익 항목을 정량적으로 비교하여 사업의 투자 타당성을 판단하는 방법이다. 일반적으로 순현재가치법(NPV)이 널리 활용되며 이를 응용한 B/C(benefit/cost) 방식, 내부수익률 등이 있다. 그러나 이러한 방법들은 투자의 불확실성(uncertainty)과 비가역성(irreversibility)을 적절히 반영하지 못하는 한계가 있다. 올바른 투자 결정을 위해서 해당 사업이 직면하는 원자재 가격 변동 등 시장의 불확실성과 매몰비용 성격의 초기 투자비에 따른 기회비용 등 다각도의 상황을 종합적으로 고려해야 한다. 실물옵션 모형은 선택의 문제를 경제성 평가에 적용한 방법으로 금융자산에 투자를 결정할 때와 같이 실물자산 투자 결정을 돕기 위해 개발되었다. 또, 전통적인 순현재가치법은 미래의 가격 변동성 등 불확실성을 반영하기 어렵다는 단점이 있다. 시장의 불확실성을 반영하기 위해 확실성등가 모형, 의사결정나무 방식, 몬테카를로 시뮬레이션 등 다양한 방법이 개발되었으나 사건 발생의 확률 선정에 대한 임의성, 사업 경과에 따른 다양한 의사결정을 고려하지 못하는 점 등이 한계로 지적된다(Park, 2018). 실물옵션은 이러한 한계를 해결할 수 있는 대안이며, 유연성 및 확장성을 가진 강력한 분석도구이다.
비용 편익의 흐름을 구체적으로 파악할 수 있어서 실물옵션 모형에 자주 이용되는 BDT 방식을 활용하여 산림에너지자립마을의 투자 타당성을 분석하였다. 산림에너지자립마을 설립에서 직면하는 불확실성의 하나는 연료비용이다. 연료로 사용하는 목재칩의 가격은 톤당 95,000원으로 설정하였다. 국산 목재칩의 가격은 국산 원목 가격 변동에 영향을 받는다.
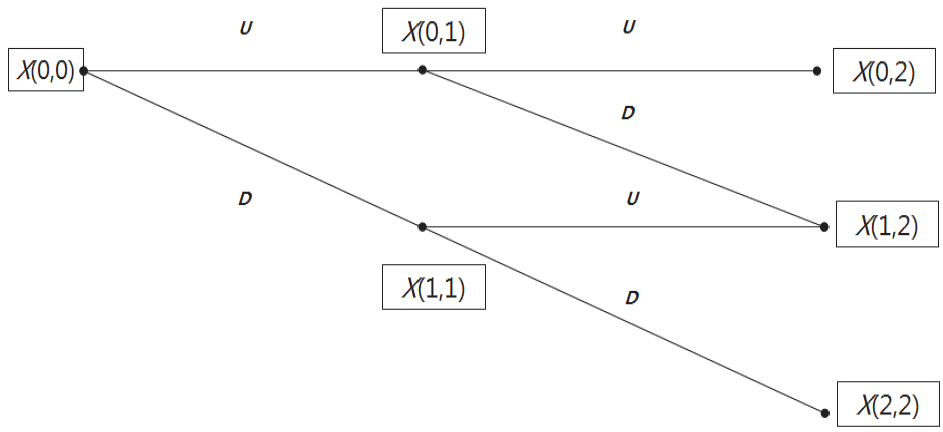
일반적으로 연료 가격이 하락하면 에너지 시설의 수익이 증가하고, 연료 가격이 상승하면 수익이 감소한다. X=(0, 0)을 현재의 목재칩 가격으로 가정하면 n노드의 목재칩 가격은 X=(i, n)으로 나타낼 수 있다. 이때 n은 시간(year)의 변화를 의미하며, i는 가격 상승 단계(upward price movement)를 의미한다. 목재칩 가격 변동성을 σ라 하면, 가격의 상승(U) 및 하락(D)폭은 , D=1/U로 계산된다(Guthrie, 2009). 이때 Δt는 시간 간격을 의미한다. 목재칩 가격은 이항나무(Binomial Tree)를 통해 전개된다. 예를 들어 만기가 2일 경우 시간에 따른 목재칩 가격 변화는 Figure 1과 같다.
목재칩 가격은 P의 확률로 증가(U)하거나, (1−P)의 확률로 하락(D)할 수 있다. 이에 따라 사업의 가치(S)도 상승하거나 하락한다. 무위험 할인율 r, 옵션행사까지의 만기 T, 초기 투자비용 K인 사업의 가치를 실물옵션으로 평가하기 위해서 만기부터 시작하여 역방향(backward)으로 계산한다. 만기의 옵션가치는 max (UiS0−K, 0)이며, 만기 이전의 옵션 가치는 max[PUi+(1−P)UiS0)e−r, UiS0−K]로 계산된다. 역방향으로 각 노드의 옵션가치를 계산하여 최종 n=0에서 사업의 옵션가치를 평가한다. 노드의 개수를 N이라 하면 이항옵션의 가치를 결정하는 공식은 다음과 같다.
목재칩 가격의 상승폭(U)과 하락폭(D), 실질적 상승확률(P)과 하락확률(1−P)을 도출하기 위해 가격변동을 결정하는 확률과정을 가정한다. 기하학적 브라운 과정(Geometric Brownian motion)과 평균회귀(Mean-reverting) 과정은 실물옵션 모형에서 자주 이용하는 확률과정이다. 기하학적 브라운 과정은 랜덤워크(random walk)를 가정하여 표류율(drift-rate)에 의존하기 때문에 가격 움직임이 무작위 행보와 같고 어떠한 수준으로 회귀하려는 성질을 갖지 않아 변동폭이 0에서 ∞로 나타날 수 있다. 그러나 평균회귀 가정은 가격이 장기 추세선을 이탈할 때 다시 회귀하는 성질을 가정하기 때문에 수요·공급의 법칙에 따라 가격이 결정되는 원자재 가격 등을 기초로 하는 사업을 분석하는 데 적합하다(Guthrie, 2009).
본 연구는 목재칩 가격 움직임을 추정하기 위해 온스타인-율렌백(Orstein-Uhlenbeck) 과정을 가정하였다(Guthrie, 2009). 원자재의 현물 가격은 주식, 채권 등 금융상품과는 달리 평균회귀적인 성질을 가지며(Routledge et al., 2000), 대표적인 평균회귀과정인 온스타인-율렌백 과정은 농산물, 목재 등 원자재 가격 예측에 다양하게 활용된다. Chaiyapa and Nattakorn(2017)은 태국의 타피오카 녹말과 홈말리 쌀 가격을 예측하는 데 온스타인-율렌백 과정을 활용하였다. 또, Plantinga(1998)의 최적 벌기령 도출 연구에서 입목가격(stumpage-price)의 온스타인-율렌백 과정을 가정하였다. 만일 입목가격이 랜덤워크 과정을 따른다면 벌채수익이 비용보다 높아 경제성이 보장되는 경우에만 옵션가치가 상승하며, 수확 유보 결정도 이같은 상황에서만 나타난다. 반면 평균회귀 과정하에서 옵션가치는 장기 평균 가격에 대비된 미래 입목가격에 따라 결정된다. 따라서 현재 가격이 장기 평균가격보다 낮다면 산주들은 향후 입목가격이 상승할 수 있음을 예상하는 등 최적의 수확시기를 예측할 수 있는 정보가 보완되어 수확 유보에 따른 인센티브가 발생한다(Plantinga, 1998). 목재칩 가격 예측에 온스타인-율렌백 프로세스를 적용한 연구는 거의 수행되지 않았으나 통계자료 등에서 일반적으로 목재칩과 입목가격의 동조현상이 관찰된다. 따라서 본 연구는 목재칩 가격 또한 입목가격과 같이 온스타인-율렌백 과정을 따른다고 가정하였다.
만일 자연로그를 취한 목재칩 가격(pj)이 식 3과 같은 AR(1) 과정을 따른다면 t시점에서 다음 Δt시점의 가격 변화는 식 4와 같은 정규분포를 따른다.
식 4에서 a는 평균회귀율(rate of mean reversion)을, b는 장기적 추세를, σ는 변동성을 의미하는 정규화 매개변수이다. Guthrie(2009)에 따라 식 5를 이용하여 정규화 매개변수를 도출할 수 있다.
식 5를 통해 도출된 정규화 매개변수를 식 6에 대입하면 가격 상승폭 U와 하락폭 D를 도출할 수 있다.
또한 n노드에서 가격의 실질적 상승확률은 아래와 같이 도출된다. 여기서 X=(i, n)은 n노드의 목재칩 가격이다.
결과 및 고찰
현재와 같이 REC가 전력생산에만 적용될 경우 산림에너지자립마을의 사업타당성을 순현재가치법과 실물옵션을 통해 평가하고 그 결과를 비교하였다. 사업의 순현재가치는 분석자료에 나타난 가격, 비용 정보(Table 1~2)와 식 1을 통해 도출하였다. 이와 동일한 정보를 의사결정의 유연성을 고려한 실물옵션가치를 도출하는 데 활용하였다. 동일한 사업에 동일한 자료를 활용하지만 실물옵션가치법은 투자자가 적절한 목재칩 가격이 발생하지 않을 시 투자를 연기하여 적절한 시기에 투자를 시행할 수 있는 유연성을 허용하고 순현재가치법과 달리 목재칩 가격의 변동성을 투자의사결정에 반영할 수 있는 장점이 있다. 투자 주체는 지자체이며, 현 정책에 따라 설비투자를 국가가 50% 보조하는 것을 가정하였다.
사업기간은 25년이며 발생하는 수익은 열과 전기 판매수입과 재생에너지원 전력에 지급하는 REC 판매수익(44.3원/KW)이며, 지출은 초기 건설비용, 연료비, 유지보수비, 보험료 및 인건비 등이다. 매년 발생하는 비용에서 유지보수비, 보험료 및 인건비 등은 고정된다고 가정한다. 목재칩 비용은 순현재가치법에서 사업기간동안 동일하다고 가정하였고, 실물옵션가치법에서는 이항나무 전개과정을 따라 매년 상승하거나 하락함을 가정하였다.
목재칩 가격의 상승폭(U)과 하락폭(D), 실질적 상승확률(P)과 하락확률(1−P)을 구하기 위해 1994~2019년의 국내 원목 가격 데이터를 활용하여 AR(1) 계수 , 및 정규화 매개변수 ,를 도출하였다. 원목 가격을 활용한 이유는 목재칩 가격에 대한 별도 통계가 존재하지 않기 때문이다. 또, 목재칩 가격은 원목 가격과 일반적으로 비례하기 때문에 변동성 추정을 위한 데이터로 적합하다고 판단하였다. 목재칩은 정책 취지에 따라 국산만을 가정하고 해외 목재칩과 대체효과 등은 고려하지 않았다. 식 3의 AR(1)모형에 따라 도출된 평균회귀과정의 매개변수와 가격 상승폭 및 하락폭은 Table 3과 같다.
| Coefficient | Description | Value |
|---|---|---|
| rate of mean reversion | 0.65 | |
| log-term trend | 11.27 | |
| volatility | 0.17 | |
| U | upward | 1.12 |
| D | downward | 0.82 |
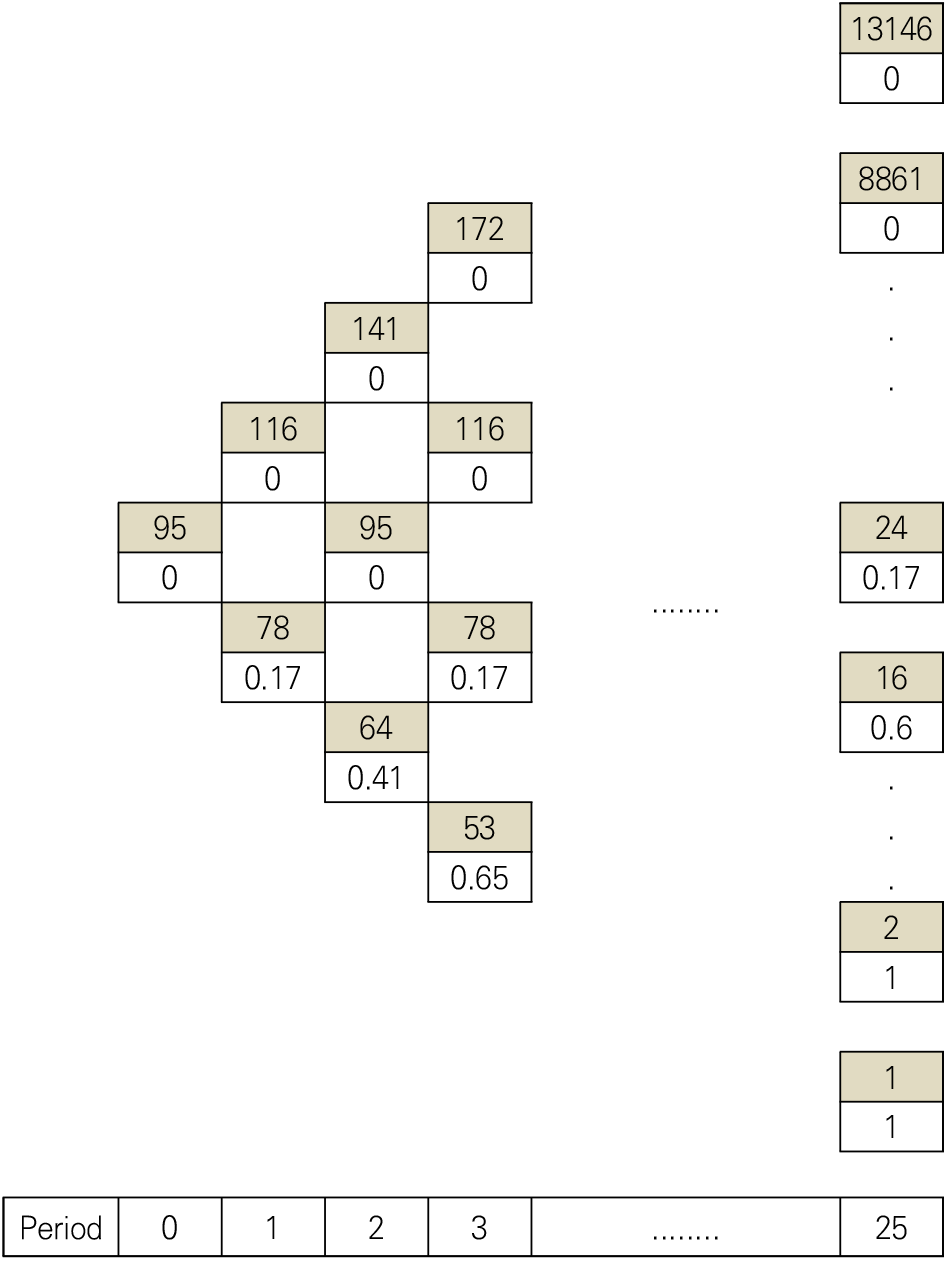
도출된 U, D와 식 7을 이용하여 추정된 기간별 목재칩 가격의 움직임과 실질적인 상승 확률 P는 Figure 2와 같다.
사업을 계획하는 지자체는 지금 당장 투자하거나, 목재칩 가격이 적정한 수준으로 하락하기를 기다려 투자를 다음으로 연기할 수 있다. 25년의 투자기간을 가정하면 옵션 만기인 마지막 연도의 옵션가치는 max(UiS0−K, 0)이다. 이때 K는 투자비용을, UiS0는 목재칩 가격 변동성을 고려한 수익의 현재가치이다. 만기 이전의 옵션 가치는 max[PUi+1S0+(1−P)UiS0)e−r, UiS0−K]로 계산되며 다음 기로 투자 결정을 미루었을 경우의 기대 수익과 당장 투자할 경우의 수익에서 큰 것을 선택한다. 이때 에너지 시설에서 얻는 수익은 순현재가치법과 마찬가지로 열과 전기 판매수입, REC 판매수입에서 운영비용을 제외한 값이다. 사업의 옵션가치를 도출하기 위한 계수는 Table 4와 같다.
| Coefficients | Description |
|---|---|
| S | revenue from the power station |
| K | initial investment |
| r | interest rate without risk |
| T | project period |
| Δt | time interval (1 year) |
순현재가치법과 실물옵션을 이용하여 평가한 사업의 투자 타당성은 Table 5와 같다. 산림에너지자립마을의 순현
| Classification | Value |
|---|---|
| NPV and IRR | -₩2,086,258 (IRR: -13.3%) |
| Option value | 0 |
재가치(NPV)와 내부수익률(IRR)은 모두 음의 값으로 나타났으며, 실물옵션 모형을 이용하여 평가한 투자가치도 0으로 도출되었다. 따라서 현재와 같이 설비에 국가보조 50%를 지원하고 전력생산에 REC 판매수익이 보장된다 하여도 수익성만 고려하면 지자체가 산림에너지자립마을에 투자하는 것이 올바른 의사결정이 아니며, 사업의 지속가능성을 위해 추가 지원이 필요함을 알 수 있다. 즉, 열 생산에도 적정 보조금 지원이 필요하다.
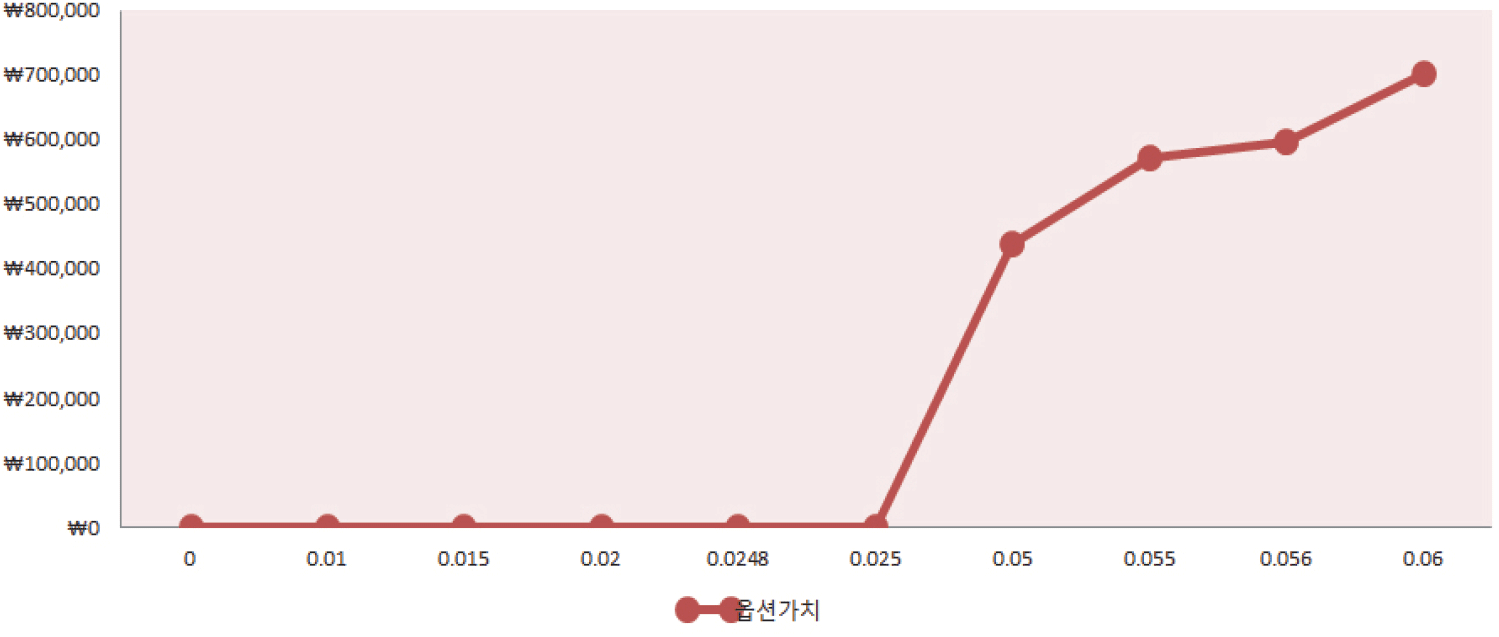
본 연구는 산림바이오매스의 에너지 활용을 위한 지원책으로 열 생산에도 적정한 보조금 지원을 제안한다. 이를 위해 적정 보조금 수준을 도출해야 한다. 본 연구는 실물옵션 가격결정모형을 활용하여 사업의 옵션가치를 0 이상으로 만드는 적정 보조금 수준을 도출하였다. 만약 열 공급에 열 보조금을 지급한다면 에너지 시설의 수익은 전기와 열 판매액에 더하여 REC 수입과 보조금의 합이 될 것이다. 시뮬레이션을 통해 열 보조금 수준에 따른 옵션가치 변화는 Figure 3과 같다. 보조금이 증가할수록 사업의 옵션가치는 증가하며, 옵션가치를 양(+)으로 전환시키는 보조금 수준은 0.0248원/kcal(24.8원/Mcal)으로 나타났다. 보조금 수준이 이보다 낮을 경우 사업의 옵션가치는 여전히 0이며 이를 기점으로 옵션가치가 양의 값으로 전환된다. 따라서 사업의 지속가능성을 위해 열 공급에 지급하여야 하는 보조금은 최소 0.0248원/kcal이어야 할 것으로 추정된다.
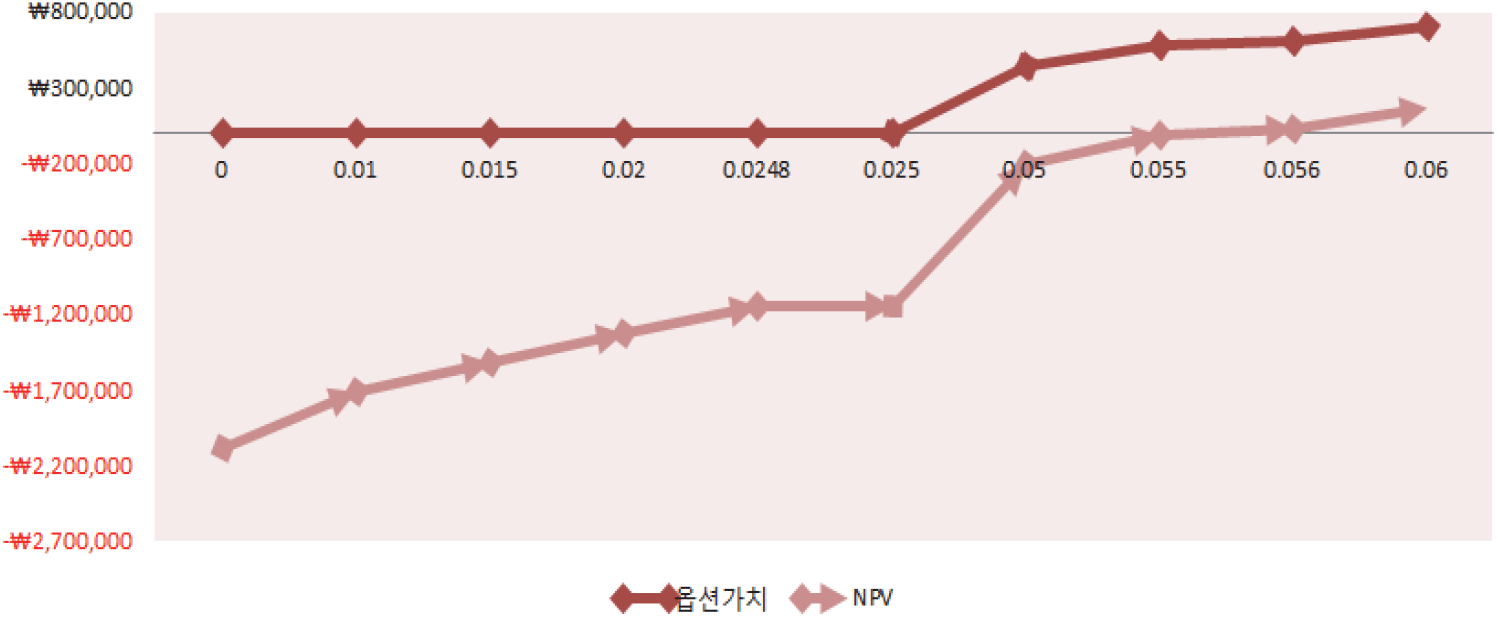
Figure 4에서는 열 보조금 지급 수준에 따른 옵션가치 변화와 순현재가치법으로 계산한 NPV 변화를 비교하였다. 옵션가치가 양의 값으로 전환되는 0.0248원/kcal의 보조금을 지급하여도 NPV는 여전히 음의 값이다. 따라서 전통적인 NPV 방식을 이용하여 평가하면 0.0248원/kcal의 보조금이 지급되어도 여전히 산림에너지자립마을사업은 수익성 없는 사업으로 평가된다. 그러나 유연성을 고려한 옵션가치로 평가하면 본 사업에 0.0248원/kcal 이상의 보조금이 지급된다면 투자가치가 있는 것으로 판단된다. NPV와 옵션가치의 차이를 불확실성의 가치(Value of uncertainty)라고 하며, 이는 적정한 투자시기를 기다림에 따라 불확실성의 완화에서 발생하는 가치이며 기다림의 가치로 표현되기도 한다(Guthrie, 2009).
Table 6은 시뮬레이션 결과를 수치로 나타내었다. NPV가 양의 값으로 전환되는 열 보조금은 0.056원/kcal 이며, NPV로 경제성을 평가할 경우 옵션가치법보다 2배 이상의 보조금을 지급해야 수익성이 있는 사업으로 평가된다. 0.0248원/kcal의 보조금 수준을 가정하면 1년 열 판매량 2,531,289.6 Mcal인 본 사업은 보조금으로 6,278만 원을 수령한다. 0.056원/kcal의 보조금 수준을 가정하면 연 1억 4,175만 원의 보조금을 수령할 수 있다. 결론적으로 열 공급에 0.0248원/kcal을 보조하면 비록 NPV로 평가된 경제성은 여전히 음의 값일지라도 유연성을 고려한 옵션가치는 양의 값을 가지기 때문에 본 사업은 투자할만한 사업이 될 것으로 판단된다.
결론 및 고찰
본 연구에서는 산림 바이오매스를 이용한 열 공급자에게 경제적 인센티브를 제공해 지속적 생산을 유도할 수 있는 열 공급 보조금을 산정하여 사업의 경제적 타당성을 확보하는 방법을 살펴보았다. 산림 바이오매스는 전력보다 열 생산에 더 적합한 연료이며 유럽 등 선진국에서도 열 에너지원으로 주로 활용된다. 또 이를 위해 다양한 지원 제도를 운영한다. 예를 들어 프랑스는 재생에너지를 통해 생산된 열의 가격을 낮게 유지하도록 지원하는 정책들을 운영하여 산림 바이오매스의 에너지 이용 확대를 유도한다. 이에 비하여 우리나라는 산림 바이오매스 에너지 이용의 지원이 주로 설비투자에 집중되어 있다. 우리나라 재생에너지 정책도 발전에만 주로 초점을 두는데, REC는 발전에만 적용되고 열 공급에는 적용되지 않는다. 순현재가치법을 통해 현재 국내에 지원되는 산림에너지자립마을 사업의 투자 타당성을 분석하고, 선택의 유연성을 고려한 콜옵션(Call option) 가격결정모형을 이용한 결과와 비교하였다. 또한 사업의 지속가능성을 위해 열 생산에 지급해야 하는 적정 보조금을 도출하였다.
현재와 같이 설비에 국비 50%를 지원하고 전력에만 REC를 인정한다면 산림에너지자립마을 열병합 발전의 순현재가치(NPV)와 내부수익률(IRR)은 모두 음(−)이며, 실물옵션 모형을 이용하여 평가한 투자가치도 0으로 도출되었다. 따라서 수익성 측면만 고려한다면 산림에너지자립마을에 투자하는 것이 올바른 의사결정이 아니며, 사업을 지속하기도 어렵다. 이 사업이 정착하고 지속가능하게 운영되려면 추가 지원이 필요함을 알 수 있다. 만일 열 공급에 REC에 상응하는 보조금을 지급한다면 열병합 발전시설의 수익은 전기와 열 판매액, REC 수입과 열 보조금의 합이 될 것이다.
시뮬레이션을 통해 도출한 사업의 옵션가치를 0보다 크게 만드는 열 보조금 수준은 최소 0.0248원/kcal으로 나타났다. 이보다 낮다면 사업의 옵션가치는 여전히 0이며 이를 기점으로 옵션가치는 양의 값으로 전환된다. 그러나 이때도 NPV는 여전히 음의 값을 가짐을 알 수 있다. 따라서 NPV 측면에서 해당 수준의 보조금으로도 사업의 투자가치를 보장할 수 없다. 그러나 유연성을 고려한 옵션가치로 평가하면 불확실성의 가치(Value of uncertainty)가 발생하기 때문에 본 사업은 투자가치가 있는 사업으로 판단된다. NPV가 양의 값으로 전환되는 열 보조금은 0.056원/kcal 이며, 옵션가치법보다 2배 이상의 보조금을 지급해야 하는 것으로 나타났다. 열 보조금이 증가한다면 투자 주체의 수익은 증가하지만 지급주체(정부)의 부담이 가중된다.
따라서 본 연구는 NPV를 양으로 전환시키는 0.056원/kcal보다 옵션가치를 양으로 전환시키는 변환점인 0.0248원/kcal가 더 적정한 열 보조금이라고 결론내고자 한다. 보조금 지급을 위한 재정 확보는 향후 추가로 고려해야 하는 과제이다. 프랑스의 열기금 사례와 같이 바이오매스의 열 공급을 지원하기 위한 기금 조성 등 재원확보를 위한 연구가 추가로 수행되어야 할 것으로 판단된다.
우리나라에서 산림 바이오매스를 이용한 열에너지 시설이 성공적으로 운영되는 사례는 아직 없고, 시행착오를 통해 성공 방안을 찾아가는 중이다. 이 연구가 그러한 과정에 조금이라도 기여하기를 기대한다.