Article
땅밀림 위험지 평가를 위한 기계학습 분류모델 비교
이제만
1, 서정일
2, 이진호
3, 임상준
1,4,*
A Performance Comparison of Machine Learning Classification Methods for Soil Creep Susceptibility Assessment
Jeman Lee
1, Jung Il Seo
2, Jin-Ho Lee
3, Sangjun Im
1,4,*
1Department of Agriculture, Forestry and Bioresources, Seoul National University, Seoul 08826, Korea
2Department of Forest Science, Kongju National University, Yesan 32439, Korea
3Division of Research, Korea Association of Forest Enviro-conservation Technology, Cheongju 28165, Korea
4Research Institute of Agriculture and Life Sciences, Seoul National University, Seoul 08826, Korea
© Copyright 2021 Korean Society of Forest Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received: Sep 16, 2021; Revised: Nov 12, 2021; Accepted: Nov 13, 2021
Published Online: Dec 31, 2021
요약
지진 발생과 집중호우에 의해 땅밀림형 산사태 유형으로 분류되는 땅밀림 현상이 전국적으로 광범위하게 나타나고 있다. 산림청은 땅밀림으로 인한 인명 및 재산 피해를 예방하기 위해 땅밀림 우려지 현장조사 판정표를 통해 땅밀림 발생 위험지를 사전에 파악하고 있다. 한편 최근에는 컴퓨터 기술의 발달로 인공지능의 한 분야인 기계학습 분류기법을 이용하여 산지재해 취약성을 평가하거나 자연재해를 예측하고 있다. 따라서 이 연구에서는 기계학습 분류기법인 k-Nearest Neighbor(k-NN), Naive Bayes(NB), Random Forest(RF), 그리고 Support Vector Machine(SVM) 분류모델을 이용하여 땅밀림 발생 위험등급을 분류하였다. 한국치산기술협회의 2018∼2020년 조사 자료 4,618개 중에서 땅밀림 현상의 발생 여부를 고려하여 발생지 총 146개소, 그리고 미발생지 146개소를 임의추출하여 292개 자료를 선정하였으며, 이 중 70%에 해당하는 204개소 자료를 훈련자료로 하여 모델을 구축하였다. 전체 자료의 30%에 해당하는 88개 검증자료에 대해 모델을 평가한 결과, k-NN은 0.727, NB는 0.750, RF는 0.807, 그리고 SVM은 0.750의 분류정확도를 보였다. 또한, Kappa 상관계수는 각각 0.534, 0.580, 0.673 및 0.585, 그리고 AUC는 각각 0.872, 0.912, 0.943 및 0.834로 계산되었다. 따라서 땅밀림 위험지역 판정을 위한 기계학습 분류모델은 RF, NB, SVM, 그리고 k-NN 순으로 높은 성능을 보였다. 기계학습 분류모델은 향후 산지토사재해의 예방 및 대응을 위한 기초자료로 활용 가능하며, 땅밀림 재해 관리 및 피해 경감에 위한 정책 개발에 필요한 정보를 제공할 것이다.
Abstract
The soil creep, primarily caused by earthquakes and torrential rainfall events, has widely occurred across the country. The Korea Forest Service attempted to quantify the soil creep susceptible areas using a discriminant value table to prevent or mitigate casualties and/or property damages in advance. With the advent of advanced computer technologies, machine learning-based classification models have been employed for managing mountainous disasters, such as landslides and debris flows. This study aims to quantify the soil creep susceptibility using several classifiers, namely the k-Nearest Neighbor (k-NN), Naive Bayes (NB), Random Forest (RF), and Support Vector Machine (SVM) models. To develop the classification models, we downscaled 292 data from 4,618 field survey data. About 70% of the selected data were used for training, with the remaining 30% used for model testing. The developed models have the classification accuracy of 0.727 for k-NN, 0.750 for NB, 0.807 for RF, and 0.750 for SVM against test datasets representing 30% of the total data. Furthermore, we estimated Cohen’s Kappa index as 0.534, 0.580, 0.673, and 0.585, with AUC values of 0.872, 0.912, 0.943, and 0.834, respectively. The machine learning-based classifications for soil creep susceptibility were RF, NB, SVM, and k-NN in that order. Our findings indicate that the machine learning classifiers can provide valuable information in establishing and implementing natural disaster management plans in mountainous areas.
Keywords: natural disaster management; soil creep; machine learning; landslide susceptibility analysis; discriminant value table
서 론
2017년 경북 포항에서 관측된 5.4 규모의 지진 영향으로 땅밀림 현상이 발생하였으며(Park et al., 2019a), 이를 계기로 지활형 산지침식인 땅밀림이 자연재해로 새롭게 부각되면서 관심이 증가하였다(Park, 2018). 한편으로, 집중호우에 의해 발생하는 땅밀림 현상도 전국적으로 광범위하게 보고되고 있다(Park et al., 2015).
우리나라에서 발생한 땅밀림은 주로 5∼20°의 완경사 산지에서 대지상을 이루는 상부 지형에서 자주 발생한다고 보고되고 있다(Park et al., 2018). 땅밀림은 붕괴형 산지침식의 한 종류인 산사태와는 달리 토층이 오랜 기간에 걸쳐 서서히 이동하기 때문에(Fairbridge, 1968; Woo et al., 1996) 발생 징후를 미리 인지하기 어려워 막대한 인명 및 재산 피해를 유발할 우려가 높다. 이러한 대규모 피해를 예방하고자 산림청과 한국치산기술협회는 땅밀림 재난 예방 및 선재대응을 위해 2018년부터 전국의 산지를 대상으로 잠재적 땅밀림 피해 위험지를 파악하고 있다.
산사태에 관한 국내·외 연구는 오랜 기간에 걸쳐 다양하게 이루어진 반면에 땅밀림에 관한 연구는 상대적으로 부족한 것이 사실이다. 이는 일부 국가에서 땅밀림을 산사태와 구별된 현상으로 보고 있지 않기 때문으로 판단된다. 일본에서는 땅밀림을 산사태와 구분되는 현상으로 규정하고 있으며, 대체적으로 땅밀림 연구가 비교적 활발하게 수행되고 있다. 특히, 일본은 Analytic Hierarchy Process (AHP) 기법을 활용하여 땅밀림 위험도, 땅밀림 피해위험도와 더불어 땅밀림 위험구역의 판정표 등을 개발하여 땅밀림 피해예방 관리 정책의 추진에 활용하고 있다. 국내의 경우 일본의 연구사례를 참고하여 국내에서 발생한 땅밀림 피해지에 대한 자료를 기반으로 땅밀림 피해면적과 발생인자 간의 상관관계를 도출하였다(Park et al., 2015, 2019b). 또한, 산림청(Korea Forest Service, 2018)은 Park et al.(2015)과 일본의 연구사례를 기초로 14개의 땅밀림 발생인자별 세부 범주를 분류하고, 이를 AHP 분석기법에 적용하여 땅밀림 발생 우려지역 판정표를 개발하였다. 이 외에도, Lee et al. (2019)는 지반조사를 통해 땅밀림지의 지하특성과 지하수와의 관계를 분석하였고, Park et al.(2020)은 인장균열을 따라 휘어져 자라는 수목의 나이테를 분석하여 땅밀림 발생 시기를 추정하는 등 다양한 방법을 통해 땅밀림의 특성을 규명하고 있다.
한편, 최근에는 컴퓨터 기술이 발달하면서 인공지능의 한 분야인 기계학습 알고리즘이 산지토사재해 취약성 분석이나 홍수재해 예측에 많이 활용되고 있다(Xu et al., 2012; Pourghasemi et al., 2013; Tehrany et al., 2015; Xiong et al., 2019; Merghadi et al., 2020). 땅밀림은 자연적 요소와 인위적 요소가 복잡하게 연관되어 있어 현상해석에 많은 양의 자료가 필요하다(Kang, 2019). 최근에는 기계학습 알고리즘이 땅밀림과 같이 복잡한 자연현상을 해석하거나 재해위험 예측 및 취약성 평가에 적용되고 있는 추세이다(Lee, 2020). Merghadi et al.(2020)은 기계학습 기반의 산사태 위험 예측 모델들의 성능을 비교한 바 있다. 그 결과 전체적으로 나무(tree) 기반 모델의 성능이 우수하며, 그 중에서도 Random Forest(RF)가 다른 기계학습 기반 모델보다 산사태 위험지 예측에 적합하다고 평가하였다. Marijanovic et al.(2009)은 산사태 위험지를 분류하기 위하여 기계학습 기반의 k-Nearest Neighbor(k-NN)와 Support Vector Machine(SVM) 모델을 적용하였으며, 그 결과 SVM의 분류 정확도가 88%로 더 높게 나타났다. 국외 사례와 비교하여 우리나라의 기계학습을 활용한 산지토사재해 분야의 연구는 매우 초보적인 수준에 머물러 있다. Vasu and Lee(2016)는 서울시 우면산을 대상으로 163개의 산사태 발생지점과 동일한 개수의 비발생지점에 대해 13개의 산사태 발생 영향인자를 추출하고, 극학습기계(extreme learning machine)를 활용한 hybrid feature selection(HFS) 기법을 이용하여 산사태 취약성을 분석하였으며, 그 결과 성공률(success rate)은 85%, 예측률(prediction rate)은 89.4%로 나타났다. Kadavi et al.(2019)은 강원도 강릉시 사천면을 대상으로 Chi-square Automatic Interaction Detection (CHAID), exhaustive CHAID, 그리고 Quick, Unbiased, Efficient, Statistical Tree(QUEST) 이상 3가지의 의사결정나무(decision tree) 모델과 더불어 로지스틱 회귀모델을 이용하여 산사태 취약성을 분석하였다. 이를 위해 762개 산사태 발생 자료와 5개 범주로 구분되는 총 20개 산사태 영향인자를 이용하여 모델을 구축하고, 산사태 위험지도를 작성하였다. 그 결과 exhaustive CHAID의 AUC가 90.6%로 가장 높았으며, CHAID와 로지스틱 회귀모델, 그리고 QUEST의 AUC는 각각 90.2%, 90.1%, 84.3%로 나타났다. 그러나 땅밀림을 대상으로 한 기계학습 기반의 연구사례는 아직까지 발표된 바 없다.
따라서, 이 연구에서는 땅밀림 발생지를 판정하기 위해 땅밀림지에서 현장조사된 자료를 이용하여 기계학습 기반의 k-NN, Naive Bayes(NB), RF, SVM 분류모델을 개발하고, 개발된 땅밀림 분류모델의 분류정확도 및 성능을 비교하여 기계학습 기반 땅밀림 위험지 평가방법을 제시하고자 하였다.
재료 및 방법
1. 자료 수집 및 전처리
땅밀림 위험지 분류모델은 기존의 땅밀림 발생지 및 미발생지에 대한 현장조사 자료를 이용하여 땅밀림 여부를 평가하는 기법으로 정의할 수 있다. 이 연구에서는 산림청의 지원을 받아 한국치산기술협회가 2018년부터 2020년까지 전국 산지를 대상으로 실시한 4,618개소의 산지사면 현장조사 자료를 이용하였다. 총 4,618개 산지사면은 현장조사 및 전문가 그룹의 심층 자문을 통해 땅밀림 발생지 여부를 판정하였으며, 이 중 3.2%에 해당하는 146개소가 땅밀림지로 최종 분류되었다.
기계학습을 이용한 분류방법은 각 범주별로 동일한 분류확률(equal opportunity)을 전제로 하기 때문에 자료의 크기는 분류 정확도에 많은 영향을 준다(Althnian et al., 2021). 즉, 모델 개발에 사용된 분류자료가 특정 범주에 편중되면 왜곡된 분류 결과를 가져와 분류 모델의 정확도가 낮아진다. 이 연구에서는 전체 공간변이를 포함하도록 자료 수가 상대적으로 많은 땅밀림 미발생지(일반산지)의 자료 수를 땅밀림 발생지와 동일한 수준으로 유지하였다. 한편, 자료의 수가 많아지며 신뢰성이 높은 모델을 구축할 수 있으나 자료 간의 자기상관성(autocorrelation)이 높아져 오히려 모델 성능이 낮아지는 경우도 있으며, 로지스틱 모델을 이용한 토석류 위험성 평가에서는 300~ 350개 공간자료가 적절한 것으로 조사되었다(Heckmann et al., 2013).
땅밀림 위험지 분류모델은 모델 개발에 사용되지 않은 독립적인 자료를 이용하여 모델의 적용성을 평가하였다(Raudys and Jain, 1991; Valalas et al., 2019). 평가에 사용되는 자료의 형태 및 수에 따라 이용되는 분류모델이 정해지며, split validation, cross validation(CV), k-fold CV, nested CV, partially nested CV 등이 주로 이용되고 있다(Valalas et al., 2019).
이 연구에서는 기계학습 분류모델을 평가하기 위해 split validation을 이용하였다. Split validation은 전체 자료를 분류 모델을 개발하는 훈련자료(training data set)와 개발된 분류모델을 검증하기 위한 검증자료(test data set)로 나누어 평가하는 방법이다. 연구에 사용된 자료는 현장조사된 146개의 땅밀림 발생지 자료를 이용하고, 같은 개수의 미발생지 데이터를 임의추출(random sampling) 방식으로 선정하여 총 292개의 분석자료를 구성하였다. 훈련자료는 292개 분석자료의 70%에 해당하는 204개 자료를 임의추출하여 사용하였으며, 나머지 30%에 해당하는 88개 자료로 모델의 성능평가를 실시하였다. Figure 1은 이 연구에서 적용된 연구방법을 개략적으로 나타낸 것이다.
분석자료는 14개의 항목(변수)으로 구성되어 있으며, 이는 땅밀림 발생 징후에 관한 2개 항목(직접징후, 간접징후), 지형에 관한 4개 항목(지형구분, 평면형(수평), 종단면형(수직), 경사), 지질에 관한 4개 항목(구성암석, 암석풍화, 불연속면과 사면의 방향성, 불연속면 간격), 토양 및 토질 4개 항목(토성, 토심, 토양수분, 너덜(talus))으로 구성되어 있다(Table 1).
Table 1.
Field survey items for assessing the soil creep susceptible area.
|
Soil Creep Factors |
Classes |
Data Category |
|
Direct Evidences |
tension crack, scarp |
Soil Creep Evidences |
|
Indirect Evidences |
structural deformation, abnormal tree growth, underground water release |
|
Topography |
gradual hill land, hill land, mountain land |
Geomorphic Characteristics |
|
Flat Horizontal |
mixed, concaved, convexed, rectilineal |
|
Longitudinal Section Vertical |
mixed, concaved, convexed, rectilineal |
|
Slope Angle |
>30°, 20~30° 10~20°, <10° |
|
Composition |
sedimentary rock, metamorphic rock, igneous rock |
Geologic Characteristics |
|
Rock Weathering |
weathered rock, soft rock, moderate rock, hard rock |
|
Discontinuity and Slope Direction |
face of slope, vertical, horizontal. reverse |
|
Discrete Surface Spacing |
very dense, dense, moderate, sparse |
|
Soil Properties at B Floor |
clay soil, sandy loam, sandy soil |
Soil Characteristics |
|
Soil Depth to B Floor |
>90 cm, 60~90 cm, 30~60 cm, <30 cm |
|
Soil Moisture |
humid, semi-humid, moderate, semi-dry, dry |
|
Talus |
absence/presence |
Download Excel Table
Table 1에 나타난 현장조사 항목별 자료의 개소수는 서로 상이하기 때문에 항목 간의 직접 비교는 어렵다. 이러한 경우에는 어떤 사건을 일으키는 요인과 발생한 사건과의 비율을 의미하는 발생빈도비(frequency ratio, FR)를 이용하여 재해위험지 분석에 널리 이용되고 있다(Oh et al., 2017). FR은 특정변수의 범주에 속하는 땅밀림 발생지가 전체 땅밀림 발생지에서 차지하는 비율을 특정변수의 범주에 속하는 조사지가 전체 조사지에서 차지하는 비율로 나눈 값으로, 특정변수의 땅밀림 발생빈도비는 식 1로 구할 수 있다.
여기서 N(cij∩L)는 변수(i)의 등급(j)에 해당하는 땅밀림 발생지 수를, N(L)는 땅밀림 발생 지점의 총 수, N(cij)는 변수(i) 각 등급(j)의 총 수, 그리고 N(S)는 전체 조사지점의 수를 의미한다.
Table 2는 Table 1에 정의된 변수의 각 범주에 대한 발생빈도비를 나타내고 있다. 직접징후에 해당하는 FR은 27.78로 가장 높게 나타났으며, 그 다음은 간접징후의 FR이 19.38로 나타나 땅밀림 사전 징후가 땅밀림 위험지 분류에 매우 중요함을 알 수 있다. 조사 변수에 대한 FR은 최소 0.32(간접징후 없음)부터 최대 27.78(직접징후 있음)까지 변화 범위가 매우 넓고, 조사변수 간에도 범주 구분에 따라 그 값이 서로 다르게 나타났다. 이렇게 조사변수 혹은 범주 간에 계산 척도가 서로 다를 경우에는 각 변수별로 범주에 해당하는 FR을 정규화하기 위한 전처리 과정이 필요하다. FR에 대한 정규화 과정은 식 2와 같다(Haung et al., 2020).
Table 2.
Normalized FR values for soil creep assessment (Lee, 2021).
|
Soil Creep Factors |
Classes |
Class ratio |
Soil Creep ratio |
Frequency ratio |
Normalized classes |
|
Composition |
metamorphic rock |
0.35 |
0.24 |
0.68 |
0.10 |
|
sedimentary rock |
0.22 |
0.37 |
1.65 |
0.90 |
|
igneous rock |
0.42 |
0.39 |
0.93 |
0.44 |
|
Rock Weathering |
hard rock |
0.09 |
0.10 |
1.10 |
0.63 |
|
moderate rock |
0.59 |
0.65 |
1.11 |
0.64 |
|
soft rock |
0.01 |
0.01 |
1.26 |
0.90 |
|
weathered rock |
0.31 |
0.24 |
0.77 |
0.10 |
|
Discontinuity and Slope Direction |
reverse |
0.58 |
0.27 |
0.47 |
0.10 |
|
vertical |
0.04 |
0.10 |
2.26 |
0.80 |
|
horizontal |
0.03 |
0.08 |
2.52 |
0.90 |
|
face of slope |
0.05 |
0.12 |
2.45 |
0.87 |
|
Discrete Surface Spacing |
very dense, |
0.02 |
0.05 |
2.03 |
0.81 |
|
dense |
0.04 |
0.08 |
2.01 |
0.80 |
|
moderate |
0.12 |
0.26 |
2.23 |
0.90 |
|
sparse |
0.68 |
0.31 |
0.45 |
0.10 |
|
Soil Depth to B Floor(cm) |
<30 |
0.11 |
0.06 |
0.55 |
0.10 |
|
30~60 |
0.62 |
0.49 |
0.78 |
0.22 |
|
60~90 |
0.22 |
0.36 |
1.63 |
0.64 |
|
>90 |
0.04 |
0.09 |
2.16 |
0.90 |
|
Soil Properties at B Floor |
sandy loam |
0.84 |
0.84 |
1.00 |
0.28 |
|
sandy soil |
0.12 |
0.06 |
0.49 |
0.10 |
|
clay soil |
0.03 |
0.10 |
2.80 |
0.90 |
|
Soil Moisture |
dry |
0.09 |
0.08 |
0.84 |
0.16 |
|
semi-dry |
0.51 |
0.37 |
0.72 |
0.10 |
|
moderate |
0.25 |
0.34 |
1.35 |
0.43 |
|
semi-humid |
0.07 |
0.16 |
2.24 |
0.90 |
|
humid |
0.07 |
0.06 |
0.74 |
0.11 |
|
Talus |
presence |
0.05 |
0.08 |
1.53 |
0.90 |
|
absence |
0.95 |
0.92 |
0.97 |
0.10 |
|
Topography |
gradual hill |
0.16 |
0.21 |
1.34 |
0.90 |
|
hill land |
0.29 |
0.28 |
0.96 |
0.57 |
|
mountain land |
0.44 |
0.19 |
0.43 |
0.10 |
|
Flat Horizontal |
concaved |
0.13 |
0.13 |
0.98 |
0.29 |
|
convexed |
0.16 |
0.20 |
1.25 |
0.90 |
|
rectilineal |
0.47 |
0.42 |
0.90 |
0.10 |
|
mixed |
0.23 |
0.25 |
1.05 |
0.45 |
|
Longitudinal Section Vertical |
concaved |
0.05 |
0.13 |
2.44 |
0.90 |
|
convexed |
0.15 |
0.14 |
0.94 |
0.13 |
|
rectilineal |
0.60 |
0.53 |
0.87 |
0.10 |
|
mixed |
0.19 |
0.20 |
1.04 |
0.19 |
|
Slope Angle |
<10° |
0.03 |
0.03 |
3.72 |
0.90 |
|
10~20° |
0.18 |
0.18 |
1.20 |
0.26 |
|
20~30° |
0.49 |
0.49 |
0.98 |
0.20 |
|
>30° |
0.19 |
0.19 |
0.59 |
0.10 |
|
Indirect Evidences |
presence |
0.03 |
0.52 |
19.38 |
0.90 |
|
absence |
0.97 |
0.48 |
0.49 |
0.10 |
|
Direct Evidences |
presence |
0.02 |
0.69 |
27.78 |
0.90 |
|
absence |
0.98 |
0.31 |
0.32 |
0.10 |
Download Excel Table
여기서, FS와 FS’는 해당 범주의 원래 FR과 정규화 이후의 FR을 의미하고, FSmn와 FSmx는 변수의 최소 및 최대 FR을 나타내며, FSub와 FSlb은 최대 및 최소 정규화 경계치를 말한다. 땅밀림 현장조사 변수의 전처리에 따른 정규화된 FR은 최소 0.1에서 최대 0.9의 값을 가지며, 그 결과는 Table 2와 같다. 여기서 class ratio는 전체 조사지 중 해당 변수가 차지하는 비율을 의미하며, 그리고 soil creep ratio는 땅밀림 발생지 중에 해당 변수가 차지하는 비율을 나타낸다.
2. 땅밀림 위험지 분류모델 개발
1) k-NN 모델
k-NN 모델은 분류(classification)나 회귀(regression) 문제에 이용되는 지도학습 분류모델이다(Liu and Zhang, 2017; Huang et al., 2020). k-NN 모델은 학습 과정이 없고 적용방법이 단순하기 때문에 최근에는 산사태와 같은 재해 위험지 평가를 위해 가장 널리 이용되고 있는 데이터 마이닝 기법이다(Haung et al., 2020).
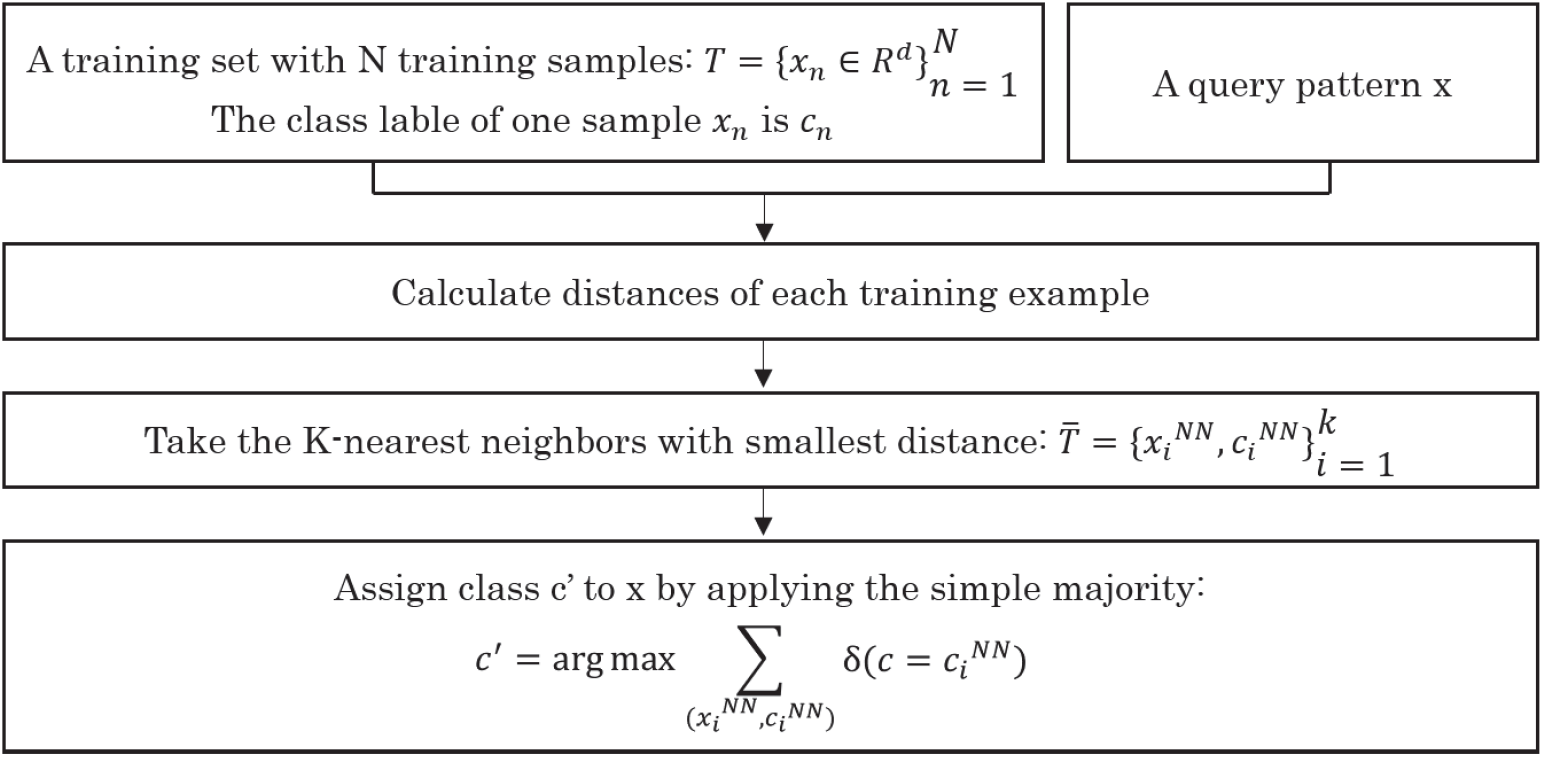
k-NN 모델의 구조는 Figure 2와 같으며, 새로운 자료와 이웃하고 있는 기존의 자료들과의 거리를 측정하여 자료 특성이 가장 유사한 k개의 자료가 동일한 범주에 포함하도록 분류하는 직관적 방법이다(Cover and Hart, 1967). 따라서 k-NN 모델은 자료를 분류하기 위해 탐색할 이웃 자료의 개수, 즉 k값과 이웃과의 거리를 측정하는 방법을 먼저 결정해야 한다. 특히, k값에 따라 분류모델의 분류 성능이 달라진다. 즉, k값이 작을수록 지역적인 자료 특성이 지나치게 반영되어 과대적합 문제(over fitting)가 나타나며, 반대로 k값이 커질수록 임의 오류(noise)에 따른 영향이 줄어들어 정확한 분류 결과를 도출하지만(Imandoust and Bolandraftar, 2013), 항목 간 경계가 불분명해지는 문제(under fitting)가 발생할 우려가 있다. 따라서, 적절한 k값을 정하기 위해 k값의 변화를 주면서 가장 뛰어난 결과를 나타내는 k값을 구해야 하는데, 이 때 일반적으로 홀수의 k값(k=1, 3, 5, 7, …)을 주로 사용하며, 또한 다양한 거리함수(distance function)를 이용하여 인접한 두 자료 간의 일치도(similarity)를 측정한다.
이 연구에서는 최적의 k값을 찾기 위해 1에서부터 1의 단위로 꾸준히 증가시키면서 분류 정확도를 평가하는 탐욕적(greedy) 방식을 적용하였다. 한편, 거리함수는 최적의 k값을 결정하는 데 중요하며, 이 연구에서는 가장 널리 사용되는 유클리안 거리함수 (euclidean distance function)를 이용하였다(Hu et al., 2016).
2) NB 모델
NB 모델은 계산의 효율성이 뛰어나고, 낮은 분산을 가지며, 새로운 훈련자료에서 파생된 낮은 차수의 확률값 추정치를 다시 적용하는 증분학습(incremental learning)이 가능하다. 또한, 사후 확률의 직접적인 예측이 가능하고, 확률을 사용하기 때문에 훈련자료의 잡음에 상대적으로 영향을 적게 받는다(Sammut and Webb, 2011).
NB 모델은 속성값 및 사건들이 서로 독립이라는 가정을 전제로 베이즈 정리(Bayes theorem)를 이용하여 특정 집단에 속할 확률을 계산한다(Tsangaratos and Ilia, 2016). 이 베이즈 정리는 식 3과 같이 사전 확률과 사후 확률의 관계로 표현된다(Mitchell, 1997; Beyene and Kamat, 2018).
여기서 X는 분류를 위해 입력된 자료의 독립변수인 x1,⋯,xn로 구성된 집합을, Ck는 각 자료의 분류를 나타낸 값을 말한다. 즉, 사전 확률과 일부의 조건부 확률이 주어진 경우, 사후 확률은 식 3을 통해 계산된다.
3) RF 모델
RF 모델은 Breiman(2001)에 의해 제안된 의사결정나무 기반의 데이터 마이닝 기법으로, 서로 다른 구조와 성능을 가지는 여러 개의 의사결정나무들을 결합하여 만들어낸 앙상블(ensemble) 모델이다. 앙상블 학습(ensemble learning)은 입력자료를 이용하여 여러 개의 모델을 학습시킨 뒤에 예측모델들을 하나로 다시 결합하는 것으로, 하나의 단일모델보다 높은 성능을 가지는 모델을 최종적으로 생성하는 기법이다.
일반적으로 단일의 의사결정나무는 훈련자료에 대해 과적합되는 경향이 있으며, 이로 인해 모델의 분류 성능이 떨어지는 한계를 가진다(Muller and Guido, 2016). RF 모델은 이러한 단일 의사결정나무의 제약조건을 극복하기 위해 배깅(bagging) 기법을 이용하여 숲(forest)을 구성하는 각 의사결정나무에 무작위성(randomness)을 부여하고, 이를 통해 의사결정나무의 예측 결과가 비상관화(decorrelation)되어 분류성능을 향상시킨다(Breiman, 2001). 배깅은 붓스트랩(bootstrap)과 결합(aggregating)의 합성어로, 다른 집단의 훈련자료를 붓스트랩 방법에 의해 학습시킨 후 다시 결합시키는 기법을 의미한다(Breiman, 1996). RF 모델은 분류와 회귀 문제 모두에 적용될 수 있으나, 범주형 예측값을 다루는 분류문제에 주로 활용되고 있다(Liaw and Wiener, 2002).
RF 모델에서 사용되는 매개변수는 크게 무작위성 제어를 위한 매개변수와 복잡도 제어를 위한 매개변수로 구분된다. 무작위성 제어를 위한 매개변수는 나무(tree)의 수(ntree)와 나무구조 설계에 사용될 최대특성수(mtry)가 있으며, 복잡도 제어를 위한 매개변수로는 나무구조의 최대깊이(max depth), 최대 리프노드의 수(max leaf nodes), 리프노드가 되기 위한 최소한의 샘플수(min samples leaf), 노드가 분기되는 최소 샘플수(min samples split) 등의 변수가 있다. RF모델의 구성하는 나무의 수나 나무의 크기가 작으면 계산 시간이 짧아지지만 정확도는 다소 떨어진다. 반면에 나무의 수와 크기가 커지게 되면 좋은 분류 결과를 얻을 수 있으나 계산 효율이 낮아지게 되므로 적절한 크기의 매개변수를 선정해야 할 필요가 있다.
4) SVM 모델
SVM 모델은 분류문제를 해결하기 위해 Cortes and Vapnik(1995)에 의해 개발된 지도학습 모형으로 최적의 결정 경계를 찾는 알고리즘이다. 즉, 결정경계(decision boundary)라는 벡터공간 내에 위치하는 자료들을 가장 잘 분류할 수 있는 자료 간의 경계를 정의하여 분류를 수행하고, 예측하고자 하는 자료가 어느 경계면에 속하는지를 확인함으로써 해당 자료의 범주를 예측하는 모형이다.
SVM 모델은 새로운 자료가 입력되었을 때, 전체 자료와의 거리 또는 유사도를 계산하는 것이 아니라 서포트 벡터와의 거리만 계산하기 때문에 계산 비용을 상당히 줄일 수 있다. 특히 이진분류의 문제를 해결하는 데 있어서 우수한 성능을 보이며, 이로 인해 현재까지도 기계학습을 적용한 자연재해 예측연구에서 가장 널리 쓰이고 있다(Xu et al., 2012; Pourghasemi et al., 2013; Tehrany et al., 2015; Xiong et al., 2019).
SVM 모델은 오분류를 일부 허용하지만 오차 혹은 비용(cost)라고 하는 매개변수를 조정하여 이를 최소화하는 경계를 찾는다. 주어진 입력속성만으로 구분할 수 있는 명확한 경계가 존재하지 않으면, 커널(kernel) 개념에 따라 새로운 변수들을 추가하여 공간을 확장시킴으로써 경계면을 구성한다. 따라서 커널에 따라 매개변수의 종류도 달라지기 때문에 최적의 매개변수를 결정하는 데 어려움이 따른다.
이상 땅밀림 분류모델 구축은 모두 오픈 소스 데이터 마이닝 시스템인 WEKA ver. 3.8.4(The University of Waikato, 2019)를 이용하였다.
3. 땅밀림 위험지 분류모델 평가
훈련된 땅밀림 위험지 분류모델의 성능을 평가하기 위해 분류정확도(accuracy)와 Kappa 상관계수, 그리고 AUC를 이용하였다. 분류정확도는 모델이 예측한 결과가 실제 결과와 비교하여 얼마나 정확하게 분류했는지를 비율로 나타낸 것으로, 전체 자료 중에서 양성(positive)으로 예측한 개수와 음성(negative)으로 예측한 개수가 차지하는 비율을 의미한다.
Kappa 상관계수는 Cohen(1968)이 제안한 방법으로 두 관찰자 간의 측정 범주값에 대한 일치도(agreement)를 측정하는 방법을 말하며, 식 4를 통해 계산할 수 있다.
여기서, K는 Kappa 상관계수이며, 0과 1 사이의 값을 가진다. PA는 분류의 일치 확률을 말하며, PC는 우연히 일치된 분류 비율을 말한다. Kappa 상관계수의 범위에 따른 일치도는 상관계수 값이 0이면 일치도가 없다고 판단하며, 1일 때는 완벽한 일치를 의미한다. 만약 K값이 음수이면 분류의 일치도가 거의 없는 상태(poor)를 나타내며, K값의 범위가 0.8∼1.0은 완벽한(almost perfect) 일치도를, 0.6∼0.8은 상당한(substantial) 일치도를, 0.4∼0.6은 적당한(moderate) 일치도를 나타낸다. 또한, 0.2∼0.4는 어느 정도(fair)의 일치도를, <0.2는 약간(slight)의 일치도를 나타낸다(Landis and Koch, 1977).
AUC란 민감도(sensitivity)와 특이도(specificity)를 이용한 지표로, 수신자 조작특성(receiver operation characteristic, ROC) 곡선을 통해 구한다. 민감도란 실제 땅밀림지가 땅밀림지로 분류된 비율이며, 특이도란 실제 비땅밀림지를 분류모델에 의해 비땅밀림지로 분류한 정도를 말한다. 임계점에 따라 재현율과 특이도가 변하게 되며, 이들의 트레이드오프(trade-off) 관계에 대해 1-특이도 값을 x축에 표시하고 민감도를 y축으로 하여 나타낸 곡선이 ROC 곡선이다. 여기서 x축과 y축은 각각 0에서 1의 범위를 가진다. ROC 곡선만으로는 분류모델의 성능을 정확하게 판단하기 어렵기 때문에 ROC 곡선이 차지하는 면적을 통해 평가한다. 실제 데이터를 샘플링한 관측값들이 이산적이므로, 입력 데이터D=(x1,y1),(x2,y2),(x3,y3),⋯,(xm,ym)에 대하여 각 이어지는 이산점들이 직선 연결 (x1=0,xm=1)이 되어 전체 곡선이 이루어진다고 할 때 AUC는 다음과 같이 계산된다(식 5).
AUC는 일반적으로 0.5∼1.0의 범위를 5등급으로 나누어 평가한다. AUC가 0.5∼0.6일 경우 분류성능 없음, 0.6∼0.7일 경우 분류성능 불량, 0.7∼0.8일 경우 보통, 0.8∼0.9일 경우 우수, 그리고 0.9∼1.0일 경우 분류성능 매우 우수로 평가한다.
결과 및 고찰
1. 다중공선성 평가
모델 개발에 앞서 자료의 다중공선성을 진단하기 위해 분산팽창지수(variance inflation factor, VIF)와 공차한계(tolerance, TOL)를 계산하였다. 다중공선성이 있으면 설명변수들 간의 선형적 상관성으로 인해 변수의 설명력이 떨어지며, 모델의 정확도도 감소하기 때문이다(Rahmati et al., 2016). VIF와 TOL은 서로 역수의 관계를 가지며, VIF가 10 보다 크거나 TOL 0.1 보다 작으면 다중공선성이 존재하는 것으로 해석한다. Table 1에 제시된 변수 간의 다중공선성 평가 결과, 모든 변수 간에는 다중공선성이 나타나지 않았다(Table 3).
Table 3.
Results of multicollinearity analysis.
|
Soil Creep Factors |
Collinearity |
Soil Creep Factors |
Collinearity |
|
TOL |
VIF |
TOL |
VIF |
|
Composition |
0.955 |
1.047 |
Talus |
0.948 |
1.055 |
|
Rock Weathering |
0.983 |
1.017 |
Topography |
0.978 |
1.023 |
|
Discontinuity and Slope Direction |
0.685 |
1.460 |
Flat Horizontal |
0.650 |
1.538 |
|
Discrete Surface Spacing |
0.711 |
1.406 |
Longitudinal Section Vertical |
0.642 |
1.557 |
|
Depth to B Floor(cm) |
0.981 |
1.019 |
Slope Angle |
0.971 |
1.030 |
|
Soil Properties at B Floor |
0.977 |
1.024 |
Indirect Signs |
0.826 |
1.211 |
|
Soil Moisture |
0.964 |
1.037 |
Direct Signs |
0.812 |
1.232 |
Download Excel Table
2. 땅밀림 위험지 분류모델의 개발
땅밀림 위험지 분류모델을 개발하기 위해서는 먼저 훈련자료를 이용하여 분류모델의 최적 매개변수를 선정하여야 한다. 이를 위하여 매개변수를 조금씩 조정하여 모델을 구축한 후 모델에 의한 분류정확도가 가장 높은 매개변수를 최적 매개변수로 결정하였다. 다만, NB 모델은 매개변수 선정이 필요하지 않기 때문에 이러한 과정을 생략하였다.
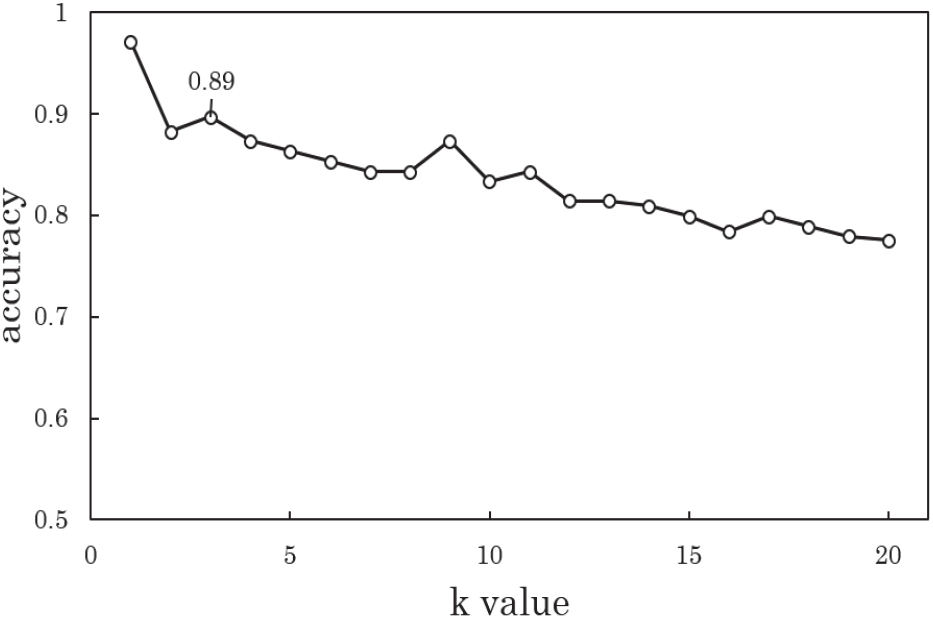
k값의 변화에 따른 k-NN 모델의 분류 결과는 Figure 3과 같다. Figure 3과 같이 70% 훈련자료를 이용하여 k값의 변화에 따른 k-NN 모델을 구축하여 비교한 결과, k값이 1일 때 분류정확도가 0.97로 가장 높게 나타났지만, k값이 1일 경우 지역적인 특성이 지나치게 반영되는 과적합의 문제가 발생할 우려가 있기 때문에(Lantz, 2013) 차순위로 높은 분류정확도인 0.89를 나타낸 k=3을 최종적으로 선정하였다.
RF 모델의 매개변수는 한 개만으로도 만족할 만한 수준의 성능을 보이며, 매개변수가 많아지면 오히려 모델의 복잡성을 증가시킨다(Muller and Guido, 2016). 따라서 이 연구에서는 RF 모델의 핵심 매개변수인 ntree와 mtry만을 사용하였다.
훈련자료를 통해 매개변수별 분류정확도를 계산한 결과, mtry=5, ntree=400의 조건에서 분류정확도가 0.995로 가장 높게 나타났다(Table 4). 변수 mtry 및 ntree를 변화시켜도 분류정확도가 크게 향상되지 않아 이 계산 조건을 RF 모델의 최적 매개변수로 결정하였다.
Table 4.
Classification accuracy of RF model.
|
mtry |
|
ntree |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
100 |
0.784 |
0.980 |
0.985 |
0.985 |
0.990 |
0.995 |
0.985 |
|
200 |
0.985 |
0.985 |
0.980 |
0.985 |
0.990 |
0.995 |
0.990 |
|
300 |
0.985 |
0.985 |
0.985 |
0.990 |
0.990 |
0.995 |
0.995 |
|
400 |
0.985 |
0.990 |
0.990 |
0.995 |
0.995 |
0.995 |
0.995 |
|
500 |
0.985 |
0.990 |
0.990 |
0.995 |
0.995 |
0.995 |
0.995 |
|
600 |
0.985 |
0.990 |
0.990 |
0.990 |
0.995 |
0.995 |
0.995 |
|
700 |
0.985 |
0.990 |
0.985 |
0.990 |
0.995 |
0.995 |
0.995 |
|
800 |
0.985 |
0.985 |
0.985 |
0.990 |
0.995 |
0.995 |
0.995 |
|
900 |
0.990 |
0.985 |
0.985 |
0.995 |
0.995 |
0.995 |
0.995 |
|
1000 |
0.985 |
0.985 |
0.985 |
0.995 |
0.995 |
0.995 |
0.995 |
Download Excel Table
SVM 모델은 다항 커널과 가우시안 커널로 구분하여 각 커널에 대한 매개변수를 결정하였다. 가우시안 커널의 매개변수는 gamma와 cost로 구성되며 gamma는 10−4, 10−3, 10−2, 10−1, 100과 같이 나누고, cost는 20, 21, 22, 23, 24으로 구분하여 분류정확도를 계산하였다. 다항 커널의 매개변수인 degree와 cost 중에서 degree는 1부터 4의 범위에서 1씩 변화를 주었으며, cost는 가우시안 커널과 동일하게 하였다.
매개변수에 따라 SVM 모델의 분류정확도를 구하면, 다항 커널의 degree=4, cost=21의 조건에서 분류정확도가 0.995로 가장 높게 나타났다(Table 5). 이후 매개변수의 조정을 함에 따라서 분류 정확도가 낮아지거나 높아지지 않았기 때문에 SVM 모델은 다항 커널에 대해 degree는 4, cost는 21을 최적 매개변수로 설정하였다.
Table 5.
Classification accuracy of SVM model with polynomial kernel.
|
degree |
|
cost |
1 |
2 |
3 |
4 |
|
20
|
0.852 |
0.911 |
0.980 |
0.990 |
|
21
|
0.857 |
0.936 |
0.990 |
0.995 |
|
22
|
0.857 |
0.951 |
0.990 |
0.995 |
|
23
|
0.852 |
0.985 |
0.995 |
0.995 |
|
24
|
0.822 |
0.990 |
0.995 |
0.995 |
Download Excel Table
3. 땅밀림 위험지 분류모델의 검증
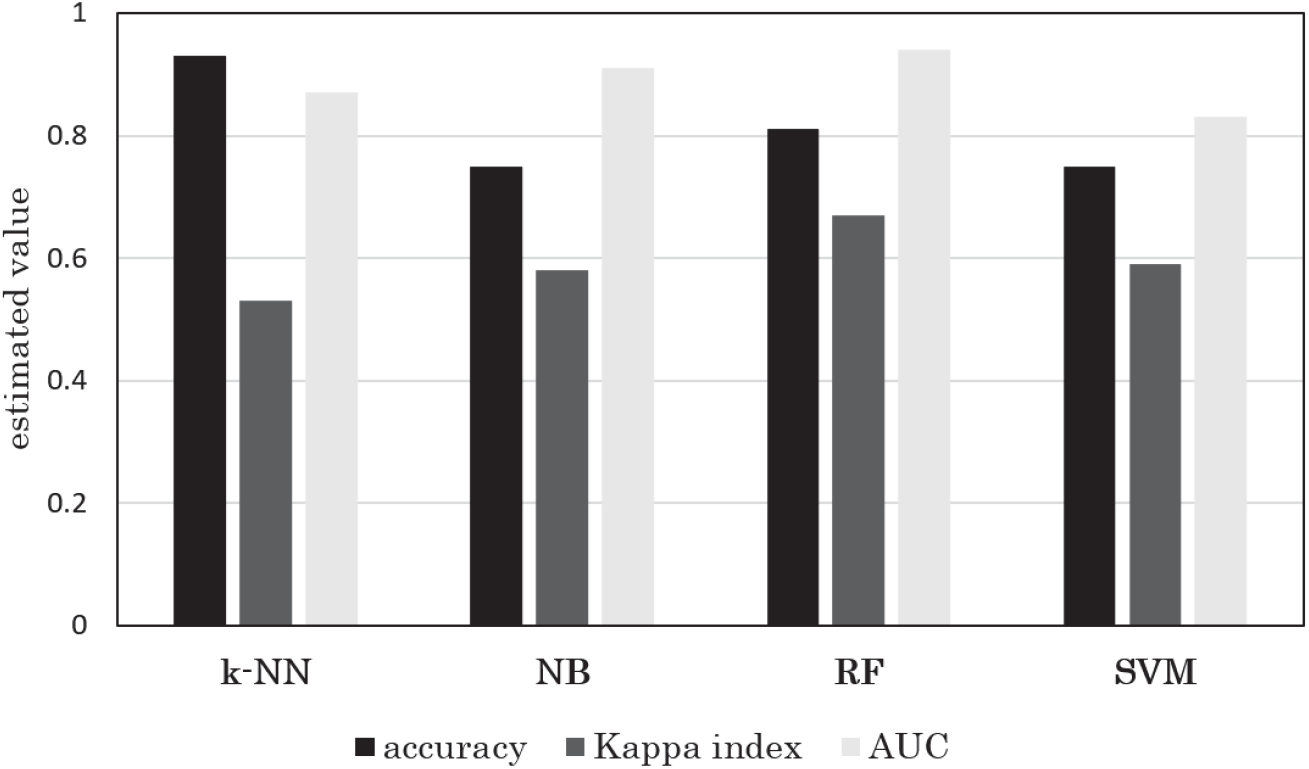
전체 조사자료 중에서 30%에 해당하는 검증자료를 이용하여 분류모델을 평가한 결과는 Figure 4와 같다. k-NN 모델의 경우 분류정확도는 0.727, Kappa 상관계수는 0.534, AUC는 0.872로 나타났다. 다음으로 NB 모델은 분류정확도 0.750, Kappa 상관계수 0.580, AUC 0.912로 평가되었다. RF 모델은 분류정확도, Kappa 상관계수 및 AUC가 각각 0.807, 0.673, 0.943로 나타났다. 마지막으로 SVM 분류모델은 분류정확도, Kappa 상관계수 및 AUC가 각각 0.750, 0.585, 0.834로 나타났다. 이와 같은 결과를 통해 땅밀림 위험지 분류모델의 성능 평가를 실시하였다. 먼저 AUC 평가를 통해 RF와 NB 모델은 ‘매우 우수’한 분류기로 평가할 수 있으며, SVM과 k-NN 모델은 ‘우수’한 분류기로 평가되었다. Kappa 상관계수를 이용한 분류 성능 평가에서는 RF 모델은 ‘상당한’ 분류 일치도를 가지는 것으로 평가되었으며, 다른 모델들은 ‘적당한’ 분류 일치도로 보여 RF 모델보다는 상대적으로 낮게 평가되었다.
RF 모델이 항상 다른 분류모델과 비교하여 우수한 분류성능을 보이는 것은 아니지만(Maroco et al., 2011; Statnikov et al., 2008), 이 연구에서는 각 평가지표에 대해 다른 분류모델보다 분류성능이 우수하게 평가되었다. 이러한 이유는 RF 모델이 대량의 데이터베이스를 효과적으로 다루며, 내부적으로 비편향된 추정치를 생성하고, 분류를 위해 각 변수들의 중요성을 추정하여 이상치를 효과적으로 탐색하기 때문이다(Rodriguez-Galiano et al., 2012).
결 론
이 연구에서는 기계학습에 기반한 분류모델을 이용하여 땅밀림 위험지를 분류하였다. 구축된 70% 현장조사 자료로부터 각 분류모델의 최적 매개변수를 설정하였으며, 독립적인 30%의 검증자료를 이용하여 구축된 분류모델의 분류성능을 평가하였다.
3가지 평가지표를 통해 종합적으로 검토한 결과, 땅밀림 위험지 분류를 위한 기계학습 기반 분류모델은 RF 모델이 가장 적합한 것으로 보이며, 다음으로는 AUC 평가에 의해 다른 모델과 비교하여 상대적으로 우수한 NB 모델이 적용가능하며, 분류정확도를 고려하여 SVM과 k-NN 모델이 다음으로 적합한 것으로 나타났다. 이 결과는 기계학습 모델을 이용한 산사태 위험지도 작성에 RF 모델이 가장 활용가치가 높았다고 평가한 Chen et al.(2018)의 연구결과와도 일치한다는 점에서 산사태 뿐만 아니라 땅밀림 위험도를 평가하기에도 RF가 가장 활용가치가 높다고 할 수 있다.
다만, 기계학습 및 훈련에 이용할 수 있는 땅밀림지 자료가 상대적으로 충분하지 않아 분류에 있어 정확도가 떨어지고 과적합이 발생할 우려가 있었다. 앞으로 땅밀림 위험지 분류의 정확도를 높이기 위해서는 땅밀림지에 대한 추가적인 자료 구축을 통해 모델을 보완할 필요가 있을 것이다. 특히, 현장자료 간의 자기상관성은 모델의 성능에 많은 영향을 미친다. 따라서, 땅밀림 위험지 평가를 위한 최적의 자료 수와 자료의 공간적 특성에 따른 모델의 성능 변화에 대한 추가 연구가 필요하다. 그리고 땅밀림 위험지를 예측하기 위한 변수 중 직접징후와 간접징후에 대한 영향이 매우 높게 나타났다. 직접적·간접적 징후가 없다면 대다수의 대상지가 미발생지로 분류된다는 것인데 추후 기계학습을 이용한 땅밀림 위험지역을 판정을 할 때 이러한 자연재해의 발생학적 특성을 고려할 필요가 있을 것이다. 그럼에도 불구하고 이 연구를 통해 구축한 분류방법은 향후 산지 재해관리를 위한 사전적 예방조치나 재해관리 대책을 수립하는 데 필요한 기초 자료를 제공할 것이다.
감사의 글
본 연구는 산림청(한국임업진흥원) 산림과학기술 연구개발사업´(2020185B10-2122-AA02)´의 지원에 의하여 이루어진 것입니다.
References
Althnian, A., AlSaeed, D., Al-Baity, H., Samha, A., Dris, A.B., Alzakari, N., Elwafa, A.A. and Kurdi, H. 2021. Impact of dataset size on classification performance: An empirical evaluation in the medical domain. Applied Sciences 11(2): 796.


Beyene, C. and Kamat, P. 2018. Survey on prediction and analysis the occurrence of heart disease using data mining techniques. International Journal of Pure and Applied Mathematics 118(8): 165-174.

Breiman, L. 1996. Bagging predictors. Machine Learning 24(2): 123-140.

,


Breiman, L. 2001. Random forests. Machine Learning 45(1): 5-32.


Cohen, J. 1968. Weighted kappa: Nominal scale agreement provision for scaled disagreement or partial credit. Psychological Bulletin 70(4): 213.

,


Cortes, C. and Vapnik, V. 1995. Support-vector networks. Machine Learning 20(3): 273-297.

,


Cover, T. and Hart, P. 1967. Nearest neighbor pattern classification. IEEE Transactions on Information Theory 13(1): 21-27.


Fairbridge, R.W. 1968. Soil creep. In: Geomorphology. Encyclopedia of Earth Science. Springer, Berlin, Heidelberg.

Heckmann, T., Grgg, K., Gegg, A. and Becht, M. 2013. Sample size matters: Investigating the effect of sample size on a logistic regression debris flow susceptibility model. Natural Hazards and Earth System Sciences 1: 2731-2779.


Hu, L.Y., Huang, M.W., Ke, S.W. and Tsai, C.F. 2016. The distance function effect on k-nearest neighbor classification for medical datasets. SpringerPlus 5(1): 1-9.

,

,


Huang, S., Huang, M. and Lyu, Y. 2020. An improved KNN-based slope stability prediction model. Advances in Civil Engineering 2020: 8894109.


Imandoust, S.B. and Bolandraftar, M. 2013. Application of k-nearest neighbor (kNN) approach for predicting economic events: Theoretical background. International Journal of Engineering Research and Applications 3(5): 605-610.

Kadavi, P.R., Lee, C.W. and Lee, S. 2019. Landslide-susceptibility mapping in Gangwon-do, South Korea, using logistic regression and decision tree models. Environmental Earth Sciences 78(4): 116.


Kang, K.H. 2019. Analysis of landslide susceptibility for Sangju and Jinbu areas using random forest model. (Dissertation). Seoul. Sejong University.

Kim, J.H. 2019. Multicollinearity and misleading statistical results. Korean Journal of Anesthesiology 72(6): 558.

,

,


Korea Forest Service. 2018. Development of extraction for land ereep susceptiile zones and field survey techniques. pp. 633.

Landis, J.R. and Koch, G.G. 1977. The measurement of observer agreement for categorical data. Biometrics. 159-174.

,


Lantz, B. 2013. Machine learning with R. Packt Publishing Ltd.

Lee, J.E. 2020. A study on improvement of map generalization using machine learning: Focusing on selective omission of building and road data. (Dissertation). Seoul. Seoul National University.

Lee, J.M. 2021. Assessment of soil creep susceptibility using machine learning classification algorithms. (Dissertation). Seoul. Seoul National University.

Lee, M.S., Park, J.H. and Park, Y.S. 2019. Analysis of characteristics using geotechnical investigation on the slow-moving landslides in the Pohang-si area. Journal of Korean Society of Forest Science 108(2): 233-240.

Liaw, A. and Wiener, M. 2002. Classification and regression by random forest. R News 2(3): 18-22.

Liu, S. and Zhang, Z. 2017. A multi-stage prediction KNN algorithm based on center vector. Computer Engineering and Science 39(9): 1758-1764.

Marjanovic, M., Bajat, B. and Kovacevic, M. 2009. Landslide susceptibility assessment with machine learning algorithms. In 2009 International Conference on Intelligent Networking and Collaborative Systems, IEEE. 273-278.


Maroco, J., Silva, D., Rodrigues, A., Guerreiro, M., Santana, I. and de Mendonca, A. 2011. Data mining methods in the prediction of dementia: A real-data comparison of the accuracy, sensitivity and specificity of linear discriminant analysis, logistic regression, neural networks, support vector machines, classification trees and random forests. BMC Research Notes 4(1): 1-14.

,

,


Merghadi, A., Yunus, A.P., Dou, J., Whiteley, J., Thaipham, B., Bui, D.T., Avtar, R. and Abderrahmane, B. 2020. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Science Reviews 207: 103-225.


Mitchell, T.M. 1997. Does machine learning really work? AI Magazine 18(3): 11-11.

Müller, A.C. and Guido, S. 2016. Introduction to machine learning with Python: A guide for data scientists. O’Reilly Media, Inc.

Oh, H.J., Lee, S. and Hong, S.M. 2017. Landslide susceptibility assessment using frequency ratio technique with iterative random sampling. Journal of Sensors. 2017.


Park, J.H. 2018. What’s land creep. Korean Society of Forest Environment Research 21: 96-107.

Park, J.H. and Park, S.G. 2020. Analysis of tree-rings for inference of periods in which slow-moving landslides occur. Journal of Korean Society of Forest Science 109(1): 62-71.

Park, J.H., Lee, C.W., Kang, M.J. and Kim, K.D. 2015. Analysis of characteristics of forest environmental factors on land creeping occurrence. Journal of Agriculture and Life Sciences 49(5): 133-144.


Park, J.H., Seo, J.I. and Lee, C.W. 2019b. Analysis of GIS for characteristics on the slow-moving landslide: With a special reference on slope and grade of landslide. Journal of Korean Society of Forest Science 108(3): 311-321.

Park, J.H., Seo, J.I., Ma, H.S., Kim, D.Y., Kang, M.J. and Kim, K.D. 2019a. Topography and soil characteristics related to land creep in 37 areas in South Korea. Journal of Korean Society of Forest Science 108(4): 540-551.

Pourghasemi, H.R., Jirandeh, A.G., Pradhan, B., Xu, C. and Gokceoglu, C. 2013. Landslide susceptibility mapping using support vector machine and GIS at the Golestan Province, Iran. Journal of Earth System Science 122(2): 349-369.


Rahmati, O., Haghizadeh, A., Pourghasemi, H.R. and Noormohamadi, F. 2016. Gully erosion susceptibility mapping: The role of GIS-based bivariate statistical models and their comparison. Natural Hazards 82(2) 1231-1258.


Raudys, S.J. and Jain, A.K. 1991. Small sample size effects in statistical pattern recognition: Recommendations for practitioners. IEEE Transactions on Pattern Analysis and Machine Intelligence 13(3): 252-264.


Rodriguez-Galiano, V.F., Ghimire, B., Rogan, J., Chica-Olmo, M. and Rigol-Sanchez, J.P. 2012. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS Journal of Photogrammetry and Remote Sensing 67: 93-104.


Sammut, C. and Webb, G.I. 2011. Encyclopedia of machine learning. Springer Science & Business Media.


Statnikov, A., Wang, L. and Aliferis, C.F. 2008. A comprehensive comparison of random forests and support vector machines for microarray-based cancer classification. BMC Bioinformatics 9(1): 1-10.

,

,


Tehrany, M.S., Pradhan, B., Mansor, S. and Ahmad, N. 2015. Flood susceptibility assessment using GIS-based support vector machine model with different kernel types. Catena 125: 91-101.


Tsangaratos, P. and Ilia, I. 2016. Comparison of a logistic regression and naïve bayes classifier in landslide susceptibility assessments: The influence of models complexity and training dataset size. Catena 145: 164-179.


Vabalas, A., Gowen, E., Poliakoff, E. and Casson, A.J. 2019. Machine learning algorithm validation with a limited sample size. PloS One 14(11): e0224365.

,

,


Vasu, N.N. and Lee, S.R. 2016. A hybrid feature selection algorithm integrating an extreme learning machine for landslide susceptibility modeling of Mt. Woomyeon, South Korea. Geomorphology 263: 50-70.


Woo, B.M., Park, J.H. Choi, H.T. Jeon, G.S. and Kim, K.H. 1996. Articles: A study on the characteristics of the landslide in Hyuseok-dong (Ⅰ): Geological and hydrological characteristics. Journal of Korean Society of Forest Science 85(4): 571-576.

Xiong, J., Sun, M., Zhang, H., Cheng, W., Yang, Y., Sun, M., Cao, Y. and Wang, J. 2019. Application of the Levenburg-Marquardt back propagation neural network approach for landslide risk assessments. Natural Hazards and Earth System Sciences 19(3): 629-653.


Xu, C., Dai, F., Xu, X. and Lee, Y.H. 2012. GIS-based support vector machine modeling of earthquake-triggered landslide susceptibility in the Jianjiang River watershed, China. Geomorphology 145: 70-80.