Journal of Korean Society of Forest Science

Korean Society of Forest Science

J. Korean Soc. For. Sci. 2022; 111(4):622-629

pISSN: 2586-6613, eISSN: 2586-6621

DOI: https://doi.org/10.14578/jkfs.2022.111.4.622

Article

맹종죽의 수간곡선식 및 수간재적표 추정

배은지¹, 손영모², 강진택³^,^*

Estimation of Stem Taper Equations and Stem Volume Table for Phyllostachys pubescens Mazel in South Korea

Eun-Ji Bae¹, Yeong-Mo Son², Jin-Taek Kang³^,^*

¹국립산림과학원 산림바이오소재연구소

²한국산지보전협회 산지연구본부

³국립산림과학원 산림ICT연구센터

¹Forest Biomaterial Research Center, National Institute of Forest Science, JinJu 52817, Korea

²Forest Research Bureau, Korea Forest Conservation Association, Daejeon 35262, Korea

³Forest ICT Research Center, National Institute of Forest Science, Seoul 02455, Korea

^*Corresponding Author E-mail: beg8bune@korea.kr

© Copyright 2022 Korean Society of Forest Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Oct 12, 2022; Revised: Nov 10, 2022; Accepted: Nov 15, 2022

Published Online: Dec 31, 2022

요약

본 연구는 우리나라 대나무 중 맹종죽에 대해 수간곡선식을 도출하고, 이를 이용하여 재적표를 개발하기 위하여 수행되었다. 맹종죽의 수간곡선식을 도출하기 위하여 Max & Burkhart, Kozak, Lee의 세 가지 수간곡선 모형을 이용하였다. 대나무는 목질 특성 상 내부가 비어 있기 때문에 수간 외직경과 내직경을 산출하고, 이를 연결하여 수간곡선화 하였다. 세 가지 수간곡선 모형을 이용하여 수간 외직경 및 내직경을 추정한 결과, Kozak 모형이 적합도지수가 가장 높고, 오차 및 편의가 가장 적어 최적 수간곡선식으로 선정되었다. Kozak 식으로 맹종죽의 수간고별 직경을 추정하고 수간곡선을 도식화하였다. 수간곡선식에 대한 잔차도를 확인한 결과, 잔차가 모두 “0”을 중심으로 분포하여 식의 적합성이 입증할 수 있었다. 맹종죽의 재적 산출을 위해 내직경, 외직경에 대해 각각 연결한 수간곡선식을 회전시켜 회전입방체를 만들었으며, Smalian 구분구적법으로 재적을 계산하였다. 외직경으로 산출된 재적에서 내직경에 의해 산출된 재적을 공제하여 맹종죽의 재적을 도출하였다. 맹종죽의 재적은 일반용재인 일본잎갈나무 재적과 비교해 볼 때, 그 양이 20∼30%에 불과한 것으로 나타났다. 그러나 맹종죽의 현재 ha당 본수와 매년 발생되는 죽순의 양을 고려한다면 개체목의 재적은 다른수종에 비해 상대적으로 적더라도, ha당 재적은 유사하거나, 오히려 더 많을 것으로 판단된다. 본 연구를 통해 국내 최초로 맹종죽의 수간곡선식 및 수간재적표가 개발되었으며, 공익 및 산업 수요 확대가 예상되는 대나무에 대한 매각 거래, 탄소흡수량 산정 등에 기초자료로 활용될 것으로 기대된다.

Abstract

The study aim was to derive a stem taper equation for Phyllostachys pubescens, a type of bamboo in South Korea, and to develop a stem volume table. To derive the stem taper equation, three stem taper models (Max & Burkhart, Kozak, and Lee) were used. Since bamboo stalks are hollow because of its woody characteristics, the outer and inner diameters of the tree were calculated, and connecting them enabled estimating the tree curves. The results of the three equations for estimating the outer and inner diameters led to selection of the Kozak model for determining the optimal stem taper because it had the highest fitness index and lowest error and bias. We used the Kozak model to estimate the diameter of Phyllostachys pubescens by stem height, which proved optimal, and drew the stem curve. After checking the residual degree in the stem taper equation, all residuals were distributed around “0”, which proved the suitability of the equation. To calculate the stem volume of Phyllostachys pubescens, a rotating cube was created by rotating the stem curve with the outer diameter at 360°, and the volume was calculated by applying Smalian’s method. The volume of Phyllostachys pubescens was calculated by deducting the inner diameter calculated volume from the outer diameter calculated volume. The volume of Phyllostachys pubescens was only 20∼30% of the volume of Larix kaempferi, which is a general species. However, considering the current trees/ha of Phyllostachys pubescens and the amount of bamboo shoots generated every year, the individual tree volume was predicted to be small, but the volume/ha was not very different or perhaps more. The significance of this study is the stem taper equation and stem volume table for Phyllostachys pubescens developed for the first time in South Korea. The results are expected to be used as basic data for bamboo trading that is in increasing public and industrial demand and carbon absorption estimation.

Keywords: bamboo; Phyllostachys pubescens; stem taper equations; stem volume table; outer and inner diameter; Fitness index

서 론

대나무는 우리 민족의 생활과 문화에 오랫동안 다양한 쓰임새를 갖고 존재해 왔으며, 특히 매화, 난초, 국화와 함께 문인화의 4군자로서 지조와 절개를 상징한다. 역사적으로 볼 때, 삼국사기에 대나무로 만든 악기가 있었던 것으로 기록되어 있고, 삼국유사 역시 죽엽군(竹葉軍), 죽현릉(竹現陵) 등의 기록 등이 있어 우리 민족과는 오랫동안 근거리에 대나무가 있어 함께하여 왔던 것으로 판단된다(The Academy of Korean Studies, 2021).

우리나라에서 자연적으로 또는 재배되고 있는 대나무 면적은 약 2만 ha로 왕대, 솜대, 맹종죽이 대부분이고, 이 중 왕대가 대부분의 면적을 차지하고 있다. 대나무는 기온이 연간 평균 10도 이상되고, 연간강수량 1,000 mm 이상되는 생육환경에서 잘 자라며, 이 때문에 주로 남부지역에 많이 분포하고 있다. 특히 맹종죽의 경우는 경남 진주, 거제 및 전남 담양 외는 생육지가 거의 나타나지 않는 것으로 조사되고 있다(National Institute of Forest Science, 2005).

대나무는 매년 죽순이 발생하고 있고, 또한 뿌리의 생장으로 인한 주변 토지로의 확장이 빨라 바이오에너지 자원으로의 활용가능성이 매우 크며, 매년 30톤 이상의 이산화탄소를 흡수한다는 보고(National Institute of Forest Science, 2020)가 있어, 기후변화에 따른 온실가스 흡수원으로써 잠재성이 높은 수종이라 할 수 있겠다.

따라서 대나무의 온실가스 능력을 보다 정밀히 평가하기 위해서는 대나무의 부피, 즉 재적(volume) 생장량이 필요한데, 현재 중량단위의 정보만 제공되고 있다(National Institute of Forest Science, 2012). 대나무의 재적 정보 획득을 위해서는 흉고직경과 수고를 변수로 하는 재적식의 개발 또는 수간곡선식을 이용하는 재적표 개발, 두 가지 방법이 있을 수 있는데, 본 연구에서는 후자의 수간곡선식을 이용하는 방법을 이용하고자 하였다.

임목의 수간(stem) 형태는 수종에 따라, 유전형질에 따라, 입목밀도 및 공간배치에 따라 각기 달리 나타나서, 이를 하나의 형태로 설명하는 것은 불가능하다. 그러나 학자들은 이들 다양한 수종에 대하여 수간의 형태를 최대한 설명하고자 수간의 외형을 수식으로 풀어 냈으며, 이것이 수간곡선식(Stem profile equation or Stem taper function)이다.

임목에 대한 수간형태는 크게 구분해보면, 그루터기 부분의 나이로이드형(neiloid), 지상부 수간을 차지하는 대부분의 부위의 포물선형(paraboloid), 수간 초두부의 원추형(conoid) 등의 3가지로 나뉜다고 볼 수 있다. 이들에 대한 일반적인 식의 형태는 y=kx^r로서, k는 간곡선율(rate of taper), r는 회전체의 형태(shape of the soild), y는 반경 또는 직경, x는 정점 또는 마지막으로부터의 거리를 나타낸다(National Institute of Forest Science, 2018a).

수간곡선식은 수간고별 직경의 크기를 단순한 수학적으로 풀어낸 것(Kozak et al., 1969; Pain and Boyer, 1996; Sharma and Oderwald, 2001)이 있는가 하면, 수간을 몇 개로 형상으로 구분하여 만든 식(Max and Burkhart, 1976; Brink and Gadow, 1986; Gadow and Hui, 1998; Cao and Wang, 2011), 그리고 수식모형의 형태를 다양한 지수식으로 만든 식(Newberry and Burkhart, 1986; Kozak, 1988, 1997, 2004; Bi, 2000)도 있었으며, 이 지수식을 수간 해석의 정확도를 높이기 위해 두 개 형태의 수식을 합쳐서 만든 식(Newnham, 1988; Kozak, 1988; Sharma and Zhang, 2004) 등 다양한 식이 존재하고 있다.

대나무는 수간 내부가 비어 있기 때문에 일반적인 임목의 수간곡선식 도출과는 다른 방법을 적용시켜야 한다. 즉, 대나무의 목질부가 있는 외부 수간형과 내부 빈공간의 수간형을 도출하여 이들 각각의 재적을 산출 한 후, 외부 수간형에서 내부 수간형을 공제한 결과를 대나무 재적 정보로 활용해야 할 것이다.

본 연구에서는 우리나라에 주로 분포하는 왕대, 솜대, 맹종죽 3종 중, 남부권역에만 자라는 맹종죽을 대상으로 최적의 수간곡선식을 도출하고자 하였으며, 또한 이를 이용하여 국내 최초의 대나무 재적표를 개발하고자 하였다.

재료 및 방법

1. 공시 재료

맹종죽 수간곡선식 산출을 위해서 경남 진주시 산림바이오소재연구소 시험림, 그리고 전남 담양군(읍)의 군유림 지역에서 분포하고 있는 대나무를 대상으로 시료를 채취하였다(Table 1). 정상적으로 생육한 대나무 숲에서 표준지를 10 m × 10 m 넓이로 구획하고, 표준지 내에서 대나무 경급별로 표준죽을 선정한 후 벌채하였다. 벌채된 대나무는 모든 가지를 제거한 후, 일정(1∼2 m) 수간고별로 구분하여 절단하였다. 목질부가 있는 수간의 외부와 내부로 각각 구분하고, 이에 대한 직경을 측정하였다. 수간 외부 평균 흉고직경은 10.7 cm, 그루터기 부위 평균직경은 12.1 cm, 평균수고는 15.6 m였다.

Table 1. Number of sample bamboos and characteristic of growth factors in surveyed area.

Species	Bamboo numbers	Diameter at breast height (cm)	Diameter at root collar (cm)	Height (m)
Phyllostachys pubescens	203	$10.7 4.9 ∼ 14.8$	$12.1 5.9 ∼ 18.2$	$15.6 7.8 ∼ 19.9$

Download Excel Table

2. 수간곡선식 도출

맹종죽의 최적 수간곡선 모델을 개발하기 위해 다양한 국가에서 많이 활용되고 있고, 기 검증된 바 있는 Max & Burkhart, Kozak, Lee 모델을 이용하였다(Tabel 2). Max & Burkhart식은 1976년 개발된 식으로서 수간을 세부분으로 나누어 2개의 변곡점을 연결하는 부분모델회귀식(segmented model regression)으로, 다양한 수종의 수간곡선 추정에 활용되고 있다(Cao et al., 1980; Parresol et al., 1986). Kozak식은 변량지수식(variable exponent taper equation, or K2 equation)으로 수간을 두 부분으로 나누어 1개의 변곡점을 갖는다. 이 변곡점(p)은 전체 수고에 대한 상대수간높이로 일반적으로 산포도를 그려 결정하게 된다. 이 식은 1988년 Kozak에 의해 개발되어 미국과 캐나다에서 널리 이용되고 있다(Figueiredo, 1995). Lee식은 우리나라에서 처음 개발된 수간곡선식(Lee, 1994)으로서 수간형태를 그루터기부터 나일로이드형, 포물선형, 포물선ㆍ원추형 및 원추형으로 구분하고, 수간형태지수를 2차방정식으로 표현하여 지수식으로 표현한 모델이다.

Table 2. Stem taper equations used for this study.

Model	Taper Equation
Max & Burkhart	$d = D B H b 1 (h H − 1) + b 2 (h 2 H 2 − 1) + b 3 (a 1 − h H) 2 I 1 + b 4 (a 2 − h H) 2 I 2$
Max & Burkhart	where	$d = diameter outside bark at height (cm) D B H = diameter at breast height outside bark (cm) h = height along stem (m) H = total height (m) b i = parameters a i = inflection points (i=1;upper, i=2;lower)$	$I i = 1, i f h H < a i 0, o t h e r w i s e$
Kozak	$d = a 1 D B H a 2 a 3 D B H X b 1 Z 2 + b 2 ln (Z + 0.001) + b 3 Z + b 4 e Z + b 5 (D B H H)$
Kozak	where	$Z = relative height (= h H) X = 1 − h H 1 − p (p = H I H, H I = inflection point) a i, b i = parameters$
Lee	$d x = b 1 · D B H 2 b · (1 − x h) [c 1 ⋅ (x h) 2 + c 2 ⋅ (x h) + c 3]$
Lee	where	$x h = relative height, b i, c i = parameters$

Download Excel Table

모델의 추정결과를 평가하기 위해, 적합도지수(Fitness index), 편의(Bias), 추정치 표준오차의 백분율(Standard error of estimate, SEE%), 평균절대편차(Mean absolute deviation, MAD) 등의 검정통계량을 이용하였다(Table 3).

Table 3. Statistical values for accuracy evaluation of stem taper equations.

Statistics	Equation
Fitness index (FI)	$F I = 1 - Σ (Y i - Y ˆ i) 2 / (Y i - Y ¯) 2$
Bias	$D ¯ = ∑ (Y i − Y^) / n$
Standard error of estimate as percent of the mean (SEE%)	$S E E % = (e i − D ¯) 2 / (N − 1) / Y ¯ × 100$
Mean absolute difference (MAD)	$D ¯ = ∑ (Y i − Y^) / n$

where Y_i, $Y i^$ , $Y ¯$ = measurement, estimate and mean of weight, repectively

n = the number of sample trees

Download Excel Table

3. 수간재적표

수간곡선은 수간의 형태를 나타내는 하나의 선이므로, 이 선을 입체로 표시해 준 것이 부피이며 재적이다. 따라서 맹종죽의 각 표본죽별 수간재적은 수간곡선 상의 수간고별 10 cm 간격으로 직경을 계산하고, 이를 원구와 말구직경을 이용하는 Smalian식에 의한 구분구적법으로 산출하였다(National Institute of Forest Science, 2018a).

결과 및 고찰

1. 맹종죽의 수간곡선식 추정

1) 수간곡선식 파라메터 도출

세 가지 수간곡선 모델을 이용하여 맹종죽에 대한 외직경(outer diameter)과 내직경(inner diameter) 수간곡선식을 도출한 결과는 Table 4와 같다.

Table 4. Parameter estimates for outer and inner diameter by stem taper equations.

Max and Burkhart			Kozak			Lee
Parameter	Outer diameter	Inner diameter	Parameter	Outer diameter	Inner diameter	Parameter	Outer diameter	Inner diameter
a1	0.4844	0.3176	a0	0.7828	0.4416	b1	1.2483	0.7103
a2	0.0291	−0.2408	a1	1.1974	1.3705	b2	0.9505	1.0528
b1	−2.7972	−1.8699	a2	0.9780	0.9726	c1	0.5245	−0.7623
b2	1.3748	0.9378	b1	1.2956	1.1016	c2	−0.5448	1.6388
b3	−1.2743	−2.8378	b2	−0.2917	−0.1417	c3	1.0113	0.0957
b4	392.8324	1714.11	b3	2.8436	2.3588	−	−	−
−	−	−	b4	−1.2922	−1.0278	−	−	−
−	−	−	b5	0.2301	0.3136	−	−	−

Download Excel Table

수간곡선 도출을 위해 이용한 세 가지 간곡선식 중, Max & Burkhart 식은 맹종죽의 수간형태를 설명함에 있어 파라메터 b₄가 식이 적합을 제대로 수렴을 하지 못해, 다소 과도한 수치가 도출되었다. 그러나 Kozak식과 Lee식은 직경의 최대크기는 나타내는 각 파라메터 a₀와 b₁가 외직경 수치가 내직경 수치보다 큰 것으로 나타나 식 적합성이 수렴된 것으로 판단된다.

2) 수간곡선식 검정

세 가지 수간곡선식 모델을 이용하여 맹종죽의 수간곡선식을 추정한 결과 Table 5와 같이 각 식별 검정통계량을 도출하였다.

Table 5. Test statistics for outer and inner diameter by stem taper equations.

Model	Max and Burkhart		Kozak		Lee
Model	Outer diameter	Inner diameter	Outer diameter	Inner diameter	Outer diameter	Inner diameter
FI*	0.9883	0.9852	0.9890	0.9865	0.9862	0.9856
SEE	0.3954	0.3576	0.3825	0.3414	0.4299	0.3530
Bias	0.0097	−0.0166	−0.0027	−0.0043	0.0045	−0.0023
MAD	0.2685	0.2601	0.2599	0.2463	0.2926	0.2545

FI : Fitness index, SEE : Standard error of estimate as percent of the mean, MAD : Mean absolute difference

Download Excel Table

이용된 세 가지 수간곡선식 모델 중, Max & Burkhart식이 하나의 파라메터가 제대로 수렴되지 못했음에도 불구하고, 외직경, 내직경의 모든 간곡선식이 적합도 98% 이상으로 높게 나타났다. 그리고 상대표준오차, 편의 등도 낮게 산출되어 세 가지 식 모두 맹종죽의 수간곡선을 설명하는데 적합한 것으로 판단되었다. 그러나, 맹종죽 재적 산출을 위하여 적합도가 다른 식보다 근소하게 높고, 오차 등의 수치가 낮은 Kozak식을 최적식으로 선정하였다.

최적식으로 선정된 Kozak식을 이용하여 맹종죽의 외직경 추정하고, 추정치에서 실측치로 뺀 값으로 외직경의 잔차를 도출하였다(Figure 1). 잔차분포가 “0”을 중심으로 고르게 분포하고 있어, Kozak식이 200여개 맹종죽 표준죽에 대한 수간고별 직경 추정을 잘 설명하고 있음을 알 수 있었다.

Figure 1. Residual scatter plot for outer diameter by relative height.

Download Original Figure

3) 맹종죽 수간곡선 형태

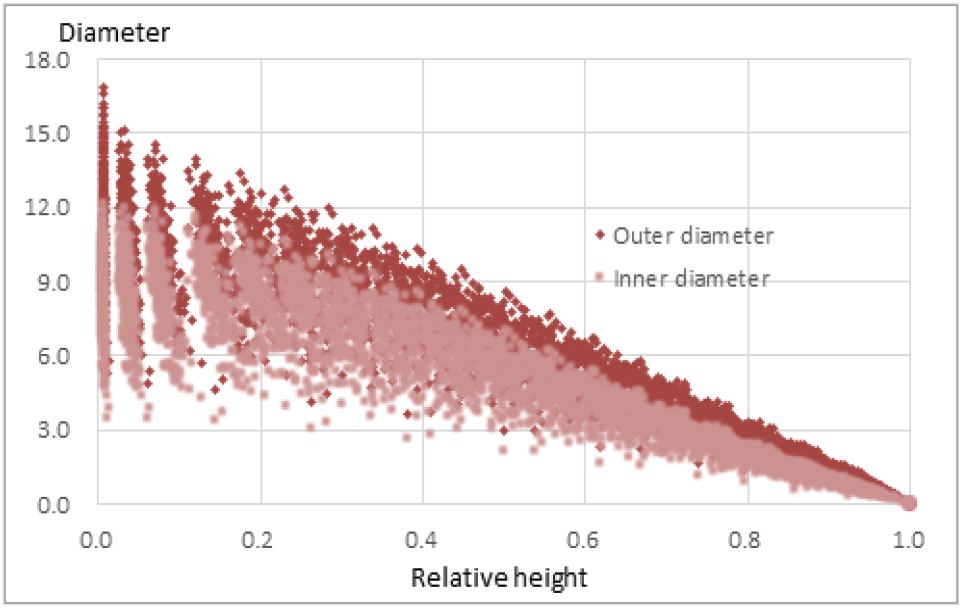
맹종죽 수간형태 설명을 위해 최적식으로 선정된 Kozak 수간곡선식 모형을 이용하여, 모든 개체죽의 외직경 및 내직경 형태를 도식화하였다(Figure 2). 상단 부분의 진하게 표시된 점들이 맹종죽의 외직경이며, 아래 부분의 엷게 표시된 점들이 내직경으로 나타났다. 맹종죽은 수간 내부가 비어있는 특징을 가지므로 외직경의 평균값에서 내직경의 평균값은 공제하여 맹종죽의 목질부위 재적을 계산하였다.

Figure 2. stem profile of outer and inner diameter by relative height.

Download Original Figure

Figure 3. Stem taper of outer and inner diameter (in the case of DBH 14 cm and height 12 m).

Download Original Figure

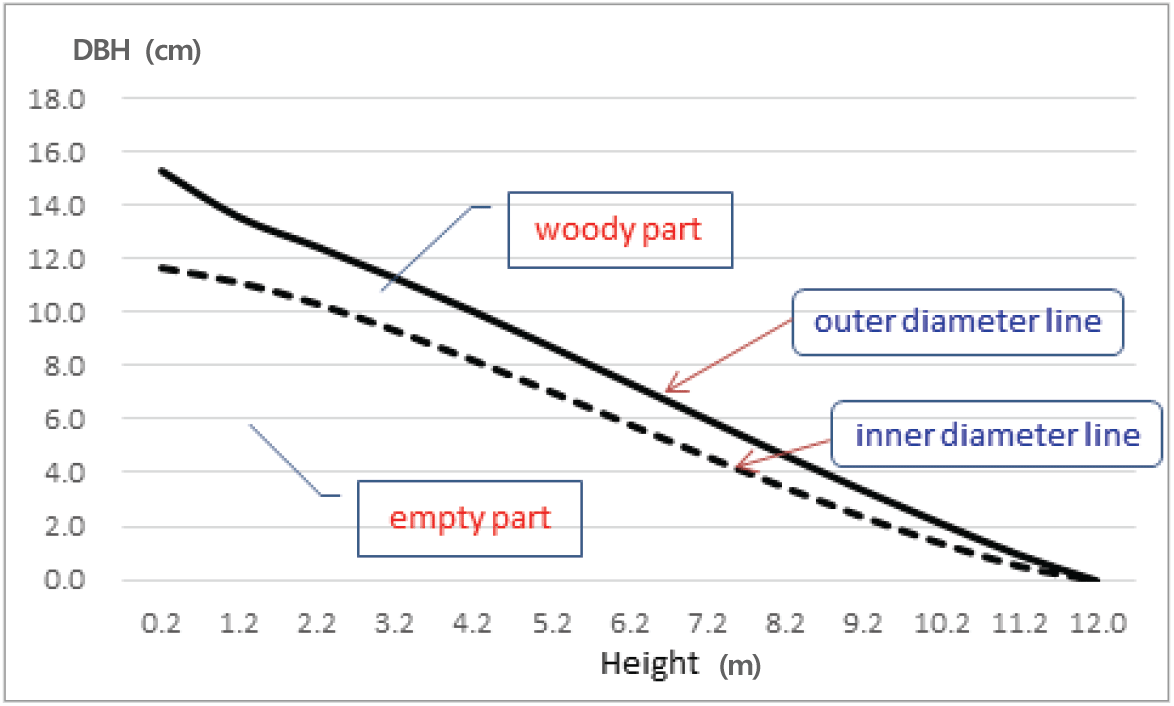
Kozak식으로 도출한 맹종죽의 외직경 및 내직경의 수간곡선을 흉고직경이 14 cm이고 수고가 12 m인 맹종죽에 적용해보면 외직경 간곡선은 그루터기 부위가 나일로이드형을 보이나, 내직경 간곡선은 일반 포물선형을 갖고 있어, 지표면에서의 맹종죽 직경생장은 안과 밖이 다소 다른 형태의 생장을 하는 것으로 판단된다.

2. 맹종죽의 수간재적 산정

대나무는 내부가 거의 비어 있기 때문에, 외부직경 곡선을 회전체로 바꾸고, 내부직경 곡선을 회전시켜, 전자에서 후자를 빼준 것이 대나무의 재적으로 산출된다. 이러한 절차 수행과 함께, 각 표본죽의 수간고별 10 cm 간격으로 직경을 Kozak식으로 추정하고, 10 cm 사이를 Smalian식에 의한 구분구적법으로 재적을 계산하고, 전체를 합하여 표본목에 대한 전체 재적으로 산출하였다(Table 6).

Table 6. Stem volume table for Phyllostachys pubescens.

H	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
D	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
3	0.0003	0.0006	0.0009	0.0011	0.0015	0.0018	0.0021	0.0024	0.0027	0.0030	0.0033	0.0035	0.0038	0.0040	0.0043	0.0045	0.0047	0.0049
4	0.0005	0.0009	0.0013	0.0017	0.0022	0.0027	0.0032	0.0037	0.0042	0.0047	0.0052	0.0056	0.0061	0.0065	0.0069	0.0073	0.0077	0.0081
5	0.0007	0.0011	0.0017	0.0023	0.0029	0.0036	0.0043	0.0050	0.0057	0.0064	0.0071	0.0078	0.0085	0.0091	0.0097	0.0103	0.0109	0.0115
6	0.0008	0.0014	0.0021	0.0029	0.0037	0.0046	0.0055	0.0064	0.0073	0.0082	0.0091	0.0100	0.0109	0.0117	0.0126	0.0134	0.0142	0.0149
7	0.0010	0.0017	0.0025	0.0035	0.0045	0.0055	0.0066	0.0077	0.0089	0.0100	0.0111	0.0122	0.0133	0.0144	0.0155	0.0165	0.0175	0.0185
8	0.0011	0.0020	0.0030	0.0041	0.0052	0.0065	0.0078	0.0091	0.0104	0.0118	0.0131	0.0145	0.0158	0.0171	0.0184	0.0196	0.0208	0.0220
9	0.0013	0.0023	0.0034	0.0046	0.0060	0.0074	0.0089	0.0105	0.0120	0.0136	0.0152	0.0167	0.0183	0.0198	0.0213	0.0227	0.0242	0.0256
10	0.0015	0.0025	0.0038	0.0052	0.0068	0.0084	0.0101	0.0118	0.0136	0.0154	0.0172	0.0189	0.0207	0.0225	0.0242	0.0259	0.0275	0.0292
11	0.0016	0.0028	0.0042	0.0058	0.0075	0.0094	0.0113	0.0132	0.0152	0.0172	0.0192	0.0212	0.0232	0.0251	0.0271	0.0290	0.0309	0.0327
12	0.0018	0.0031	0.0047	0.0064	0.0083	0.0103	0.0124	0.0146	0.0168	0.0190	0.0212	0.0234	0.0256	0.0278	0.0300	0.0321	0.0342	0.0363
13	0.0019	0.0034	0.0051	0.0070	0.0091	0.0113	0.0136	0.0159	0.0183	0.0208	0.0232	0.0256	0.0281	0.0305	0.0329	0.0352	0.0376	0.0398
14	0.0021	0.0037	0.0055	0.0076	0.0099	0.0122	0.0147	0.0173	0.0199	0.0226	0.0252	0.0279	0.0305	0.0331	0.0358	0.0383	0.0409	0.0434
15	0.0023	0.0039	0.0059	0.0082	0.0106	0.0132	0.0159	0.0187	0.0215	0.0244	0.0272	0.0301	0.0330	0.0358	0.0386	0.0414	0.0442	0.0469
16	0.0024	0.0042	0.0064	0.0088	0.0114	0.0142	0.0171	0.0200	0.0231	0.0262	0.0292	0.0323	0.0354	0.0385	0.0415	0.0445	0.0475	0.0505
17	0.0026	0.0045	0.0068	0.0094	0.0122	0.0151	0.0182	0.0214	0.0247	0.0279	0.0312	0.0345	0.0378	0.0411	0.0444	0.0476	0.0508	0.0540
18	0.0027	0.0048	0.0072	0.0100	0.0129	0.0161	0.0194	0.0228	0.0262	0.0297	0.0332	0.0368	0.0403	0.0438	0.0472	0.0507	0.0541	0.0575
19	0.0029	0.0051	0.0076	0.0105	0.0137	0.0171	0.0206	0.0241	0.0278	0.0315	0.0352	0.0390	0.0427	0.0464	0.0501	0.0538	0.0574	0.0610
20	0.0031	0.0053	0.0081	0.0111	0.0145	0.0180	0.0217	0.0255	0.0294	0.0333	0.0372	0.0412	0.0451	0.0491	0.0530	0.0568	0.0607	0.0645
21	0.0032	0.0056	0.0085	0.0117	0.0152	0.0190	0.0229	0.0269	0.0310	0.0351	0.0392	0.0434	0.0476	0.0517	0.0558	0.0599	0.0640	0.0680
22	0.0034	0.0059	0.0089	0.0123	0.0160	0.0199	0.0240	0.0282	0.0325	0.0369	0.0412	0.0456	0.0500	0.0544	0.0587	0.0630	0.0673	0.0715
23	0.0036	0.0062	0.0093	0.0129	0.0168	0.0209	0.0252	0.0296	0.0341	0.0387	0.0432	0.0478	0.0524	0.0570	0.0615	0.0661	0.0705	0.0750
24	0.0037	0.0065	0.0098	0.0135	0.0176	0.0219	0.0264	0.0310	0.0357	0.0404	0.0452	0.0500	0.0548	0.0596	0.0644	0.0691	0.0738	0.0785
25	0.0039	0.0067	0.0102	0.0141	0.0183	0.0228	0.0275	0.0323	0.0373	0.0422	0.0472	0.0523	0.0573	0.0623	0.0672	0.0722	0.0771	0.0819

H: Height (m), D: F.I. : Diameter at breast height outside bark (cm)

Download Excel Table

맹종죽 수간재적표를 수간이 곧게 자라면서 내부가 목질부로 차 있는 일본잎갈나무(National Institute of Forest Science, 2018b)의 몇 개 직경 및 수고급별 재적과 비교해 보았다(Table 7).

Table 7. Volume comparison between Phyllostachys pubescens and Larix kaepferi.

DBH (cm)	Height (m)	Phyllostachys pubescens (m³)	Larix kaempferi (m³)	Volume difference (base, Larix kaepferi)
6	5	0.0023	0.0076	30.3%
12	14	0.0226	0.0827	27.3%
20	22	0.0715	0.3438	20.8%

Download Excel Table

맹종죽의 경우, 재적은 내부가 텅 빈 관계로 목질부가 가득 차 있는 일본잎갈나무에 비해 직경이 적은 나무는 약 30%, 직경이 큰 나무는 약 20%에 불과한 것으로 나타 났다. 이와 같은 결과는 맹종죽이 일본잎갈나무의 재적과 동일한 양이 되려면 동일 직경급의 3∼5 그루가 있어야 한다는 것이다. 그러나 보통 대나무 숲은 ha당 10,000∼15,000본의 밀도를 보이고 있으므로 ha당 재적은 유사할 것으로 판단된다. 또한 새로운 죽순은 매년 지속적으로 발생하므로 대나무 숲의 바이오매스는 일반용재보다 많을 것으로 판단된다.

결 론

기존 산업용으로 사용되는 대나무의 매각 거래는 중량단위로 거래되어 왔으나 최근 바이오에너지 자원, 온실가스 흡수원으로써 가치가 높은 대나무에 대해 온실가스 통계량 산정을 위해 부피(재적) 단위의 정보가 필요하게 되었다. 그러나 수간 내부가 비어있는 대나무를 대상으로 재적을 산정하는 연구는 수행된 바 없어 재적정보를 도출할 수 있는 효과적인 방법을 적용하는 것이 중요하다. 본 연구에서는 일반 용재수종의 재적 산출을 위한 수간곡선식을 이용하는 방법을 적용하였으며 맹종죽의 재적 도출 적합성을 판단하고자 하였다.

맹종죽 수간의 바깥 부분인 외직경 곡선을 도출하고, 또한 목질부가 끝나는 내부직경의 곡선을 도출하여 두 곡선을 회전입방체로 만들어, Smalian 구분구적식으로 각각의 재적을 산출하는 과정을 거쳤다. 최종적으로 맹종죽의 재적은 외직경 곡선에 의해 도출된 재적(A)에서 내직경 곡선에 의해 도출된 재적(B)을 뺀 값(A-B, 순수 목질부)으로 산출하게 되었다.

본 연구 결과 맹종죽의 재적은 수간 내부가 비어있는 이유로 내부가 차있는 일반용재 재적보다 당연히 적었으며, 동일 직경급일 경우, 맹종죽 3∼5 그루가 일반용재 1 그루의 재적과 유사한 양이 됨을 밝혀냈다. 또한 대나무의 입목밀도가 일반 용재수종 보다 월등히 높고, 매년 발생되는 죽순으로 바이오매스는 대나무가 더 많을 것으로 판단된다.

2050 탄소중립 추진 전략 실현을 위하여 국내 산림자원에 대한 온실가스 흡수원 평가 및 탄소량 전환 연구는 매우 중요하다 할 수 있다. 대나무는 목재기본밀도가 참나무와 유사한 수준이며, 단위면적 당 높은 입목밀도, 지속적인 죽순 생산 등의 사유로 연간 탄소흡수량이 다른 일반 수종보다 높게 측정될 것으로 판단된다. 따라서 대나무의 탄소량 전환 연구를 위해 본 연구에서 도출된 수간재적정보 외에도 목재기본밀도, 바이오매스 확장계수, 뿌리함량비 등의 탄소전환계수 정보를 구축할 수 있는 추가 연구가 필요할 것으로 판단된다. 본 연구는 우리나라 주요 대나무 중 직경생장이 가장 우수하며, 죽순, 문구류, 조형물 등에 다양하게 활용되고 바이오에너지 자원, 온실가스 흡수원으로써 가치가 높은 맹종죽을 대상으로 수간곡선식 및 수간재적표를 개발하여 매각 거래, 탄소흡수량 산정 등의 공익 및 산업 수요 확대에 대응하기 위한 기초자료를 활용될 것으로 기대된다.

감사의 글

본 연구는 산림청 국립산림과학원 일반연구과제 연구비로 수행되었음(과제번호:FM0000-2020-01-2021).

References

Bi, H. and Turner, J. 1994. Long-term effects of superphosphate fertilization on stem form, taper and stem volume estimation of Pinus radiata. Forest Ecology and Management 70(1-3): 285-297.

Brink, C. and Gadow, KV. 1986. On the use of growth and decay functions for modeling stem profiles. EDV in Medizin Biologie 17(1/2): 20-27.

Cao, Q.V. and Wang, J. 2011. Calibrating fixed- and mixed-effects taper equations. Forest Ecology and Management 262(4): 671-673.

Cao, Q.V. Burkhart, H.E. and Max, T.A. 1980. Evaluation of two methods for cubic-volume prediction of loblolly pine to any merchantable limit. Forest Science 26(1): 71-80.

Figueiredo-Filhoa, A, Bordersb, B.E. and Hitchb, K.L. 1996. Taper equations for Pinus taeda plantations in Southern Brazil. Forest Ecology and Management 83(1-2): 39-46.

Gadow, K.V. and Hui, G.Y. 1998. Modelling forest development. Dordrecht: Kluwer Academic Publishers.

Kozak, A., Munro, D.D. and Smith, J.H.G. 1969. Taper functions and their application in forest inventory. The Forestry Chronicle 45(4): 278-283.

Kozak, A. 1988. A variable-exponent taper equation. Canadian Journal of Forest Research 18(11): 1363-1368.

Kozak, A. 1997. Effects of multicollinearity and autocorrelation on the variable-exponent taper functions. Canadian Journal of Forest Research 27(5): 619-629.

10.

Kozak, A. 2004. My last words on taper equations. Forestry Chronicles 80(4): 507-515.

11.

Lee, W.K. 1994. Stem and stand taper model using spline function and linear equation. Korean Society of Forest Science 83(1):63-74.

12.

Max, T.A. and Burkhart, H.E. 1976. Segmented polynomial regression applied to taper equations. Forest Science 22(3): 283-289.

13.

National Institute of Forest Science. 2005. Everything in the bamboo. National Institute of Forest Science, New research book, No. 7, pp. 191.

14.

National Institute of Forest Science. 2012. Guideline of standard carbon absorption. in internal data of NIFoS.

15.

National Institute of Forest Science. 2018a. Guidline of forest mesurement and survey. National Institute of Forest Science, New research book, No. 113, pp. 191.

16.

National Institute of Forest Science. 2018b. Stem volume, biomass and stand yield table. National Institute of Forest Science, Research book, pp. 221.

17.

National Institute of Forest Science. 2020. GHG absorption of bamboo. Public relations of NIFoS.

18.

Newberry, J.D. and Burkhart, H.E. 1986. Variable-form stem profile models for loblolly pine. Canadian Journal of Forest Research 16(1): 109-114.

19.

Newnham, R.M. 1988. A variable-form taper function. Canada Forest Service. Information Report PI-X-083. Chalk River: Forestry Canada, Petawawa National Forestry Institute pp. 1-33.

20.

Pain, O. and Boyer, E. 1996. A whole individual tree growth model for Norway spruce. In: Workshop IUFRO S5. Nancy: INRI-Nancy. 01-04-Topic 1.

21.

Parresol, B.R., Hotvedt, J.E. and Cao, Q.V. 1986. A volume and taper prediction system for bald cypress. Canadian Journal of Forest Research 17(3): 250-259.

22.

Sharma, M. and Oderwald, R.G. 2001. Dimensionally compatible volume and taper equations. Canadian Journal of Forest Research 31(5): 797-803.

23.

Sharma, M. and Zhang, S.Y. 2004. Variable-exponent taper equations for jack pine, black spruce, and balsam fir in eastern Canada. Forest Ecology and Management 198(1-3): 39-53.

24.

The Academy of Korean Studies. 2021. Encyclopedia of Korean Culture (in Website).