난대지역 붉가시나무의 수간곡선식 도출 및 수간재적표 작성

붉가시나무 수간곡선식 도출 및 수간재적표 작성을 위하여 조사, 측정된 입목 개체수는 총 688본이었는데, 조자자료는 2007년부터 현재까지 국립산림과학원에서 수집된 모든 자료를 취합한 것이다. 이들은 경남 고성과 진주, 전남 완도, 그리고 제주 서귀포 등지에서 정상적으로 생육하고 있는 개체목을 대상으로 입목을 벌목하여, 현장에서 수간고 0.2 m, 1.2 m. 3.2 m, 5.2 m….에서 수피를 포함한 직경을 각각 측정하였다. 그리고 이들 부위에서 원판을 채취하여 실험실로 이동한 후, 수간석해에 의한 방법에 의해 5년 단위로 수간고별 직경 자료를 측정하였다. 5년 단위의 원판 내부에서 측정되는 직경은 수피에 대한 정보가 없기 때문에, 수피가 측정된 원판 자료를 모두 모아 수간고 직경별 수피두께 추정식을 만들어 적용하였다.

Table 1에서, 조사된 개체목의 흉고직경급은 최대 약 33 cm, 수고는 약 17 m 였으며, 수령은 54년생까지 분포하는 것으로 나타났다.

3가지 수간곡선 모형을 이용하여 붉가시나무 수간곡선식을 도출한 결과, Table 4와 같이 각 모형별 파라미터 및 검정통계량을 산출할 수 있었다.

Table 4에서 Kozak 모형이 적합도지수 및 기타 검정통계량 값에 있어 가장 우수함을 알 수 있었으며, 이 모형이 붉가시나무 수간곡선을 추정하는데 있어 최적식임을 알 수 있었다. 국내외 학술연구에서도 수종별 수간곡선을 설명함에 있어 Kozak 모델이 최적임을 제시한 사례가 다수 존재하고 있다(Son et al., 2002; Lee et al., 2014; Chiu et al., 2015; Shahzad et al., 2020; Sandoval et al., 2022).

Kozak 모형으로 붉가시나무 수간곡선을 도출한 연구는 2007년에 Son et al.(2007)이 수행한 바 있고, 2010년에는 Chung et al.(2010)에 의해 연구된 바 있는데, 2007년에 수행한 연구에서의 Kozak 모형의 변곡점은 0.25, 2010년은 0.22로 나타난 것으로 보고되었다. 금번 연구는 0.20이었는데, 즉 수간의 상대적인 높이인 20% 수준에서 변곡점이 형성되는 것으로 나타났다. 이는 동일 수종이라 하더라도 연구자의 관점 또는 조사된 자료의 특징에 따라 수간형태가 달라질 수 있음을 보여 주는 사례라 볼 수 있겠다.

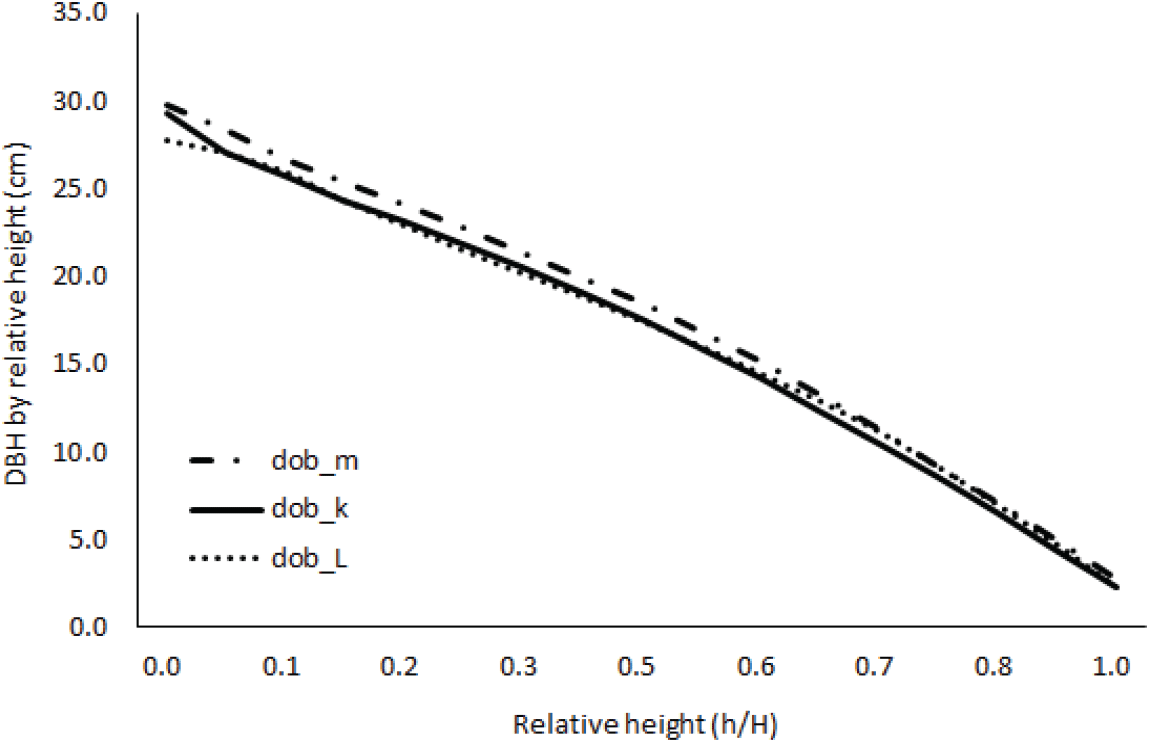
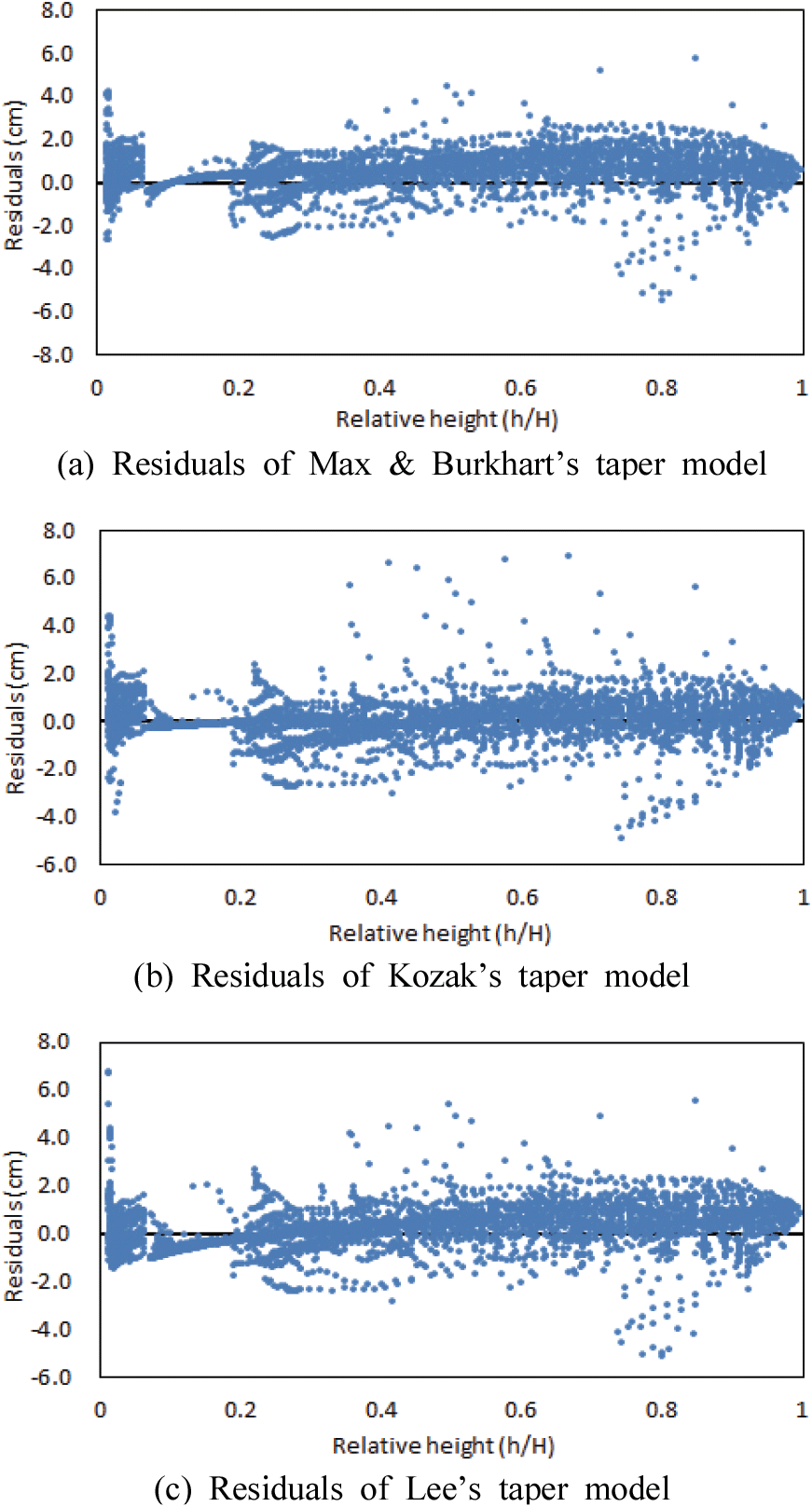
Max & Burkhart 모형, Kozak 모형, Lee 모형을 이용하여 표준목을 대상으로 수간곡선을 도식화한 바 Figure 1과 같다. 3가지 모형으로 표현된 상대수고별 직경의 분포 패턴은 유사한 것으로 나타났다. 다만 Figure 1로만 볼 때, Max & Burkhart 모형으로 붉가시나무의 직경을 도출할 시, 다른 두 개 모형보다 상대수간고 중앙부위 이하에서는 직경이 더 큰 값을 보일 수도 있음을 알 수 있었다. 이런 가시적인 현상을 정확하게 판단할 수 있는 것이 잔차분석인데, 우리가 사용한 3개 모형들이 실측치를 얼마나 잘 설명해 줄 수 있는 지에 대한 잔차분포를 Figure 2와 같이 도식화 하였다.

Figure 1. Stem taper curve pattern by taper models. (Note) dob: Diameter outside bark (cm), dob_m: Stem taper curve presented in Max & Burkhart model, dob_k: Kozak model, dob_L: Lee model

Download Original Figure

Figure 2. Residual error scattergram for the diameter estimation by stem taper models.

Download Original Figure

Figure 2에서 Max & Burkhart 모형과 Lee 모형은 그루터기 부분의 직경을 과소 추정하고 있으며, 상대수고(relative height) 약 50% 이상부터는 과소 추정하고 있음을 알 수 있었다. 잔차도 그림에서 보다시피, 이 두가지 모형의 찬차분포가 “0”을 중심으로 위쪽에 분포하고 있음을 확인할 수 있다. 이에 반해 Kozak 모형은 앞선 두 모델과는 달리 그루터기 부분의 직경은 잘 설명하고 있었으며, 상대수고 전반에서 잔차도 “0”을 중심으로 상하 균형적으로 잔차가 분포하고 있음을 확인할 수 있었다. 결론적으로 세 모형의 잔차분포에서도 역시 Kozak 모형이 붉가시나무의 수간고별 직경을 추정하는데 최적임을 알 수 있었다.

Kozak 수간곡선모형을 이용하여 붉가시나무의 수간재적표를 작성할 수 있으며, 그 중 일부 구간의 재적표를 Table 5와 같이 표현할 수 있었다. 이 표를 이용하면 붉가시나무의 흉고직경과 수고에 따른 단목 재적을 얻을 수 있을 것이며, 용재의 매각 거래에 물량을 산정하는 기준이 될 수 있을 것이다. 본 붉가시나무 재적표는 그간 일부 지역 즉, 완도 수목원 지역만의 조사(Son et al., 2007)와 제주도 지역만의 조사(Chung et al., 2010) 분석결과와는 다르게 이들 자료를 포함함은 물론이고, 전남 완도지역에 서의 추가 자료수집 및 전남 해남군, 경남 고성군 및 진주시 시험지 등에서의 수간석해 자료를 모두 포함하였기 때문에 현 수준에서는 공식적으로 붉가시나무 재적표로 활용할 수 있을 것이라 판단된다.

상기 언급한 바 있지만, 2007년과 2010년에 붉가시나무에 대해 수간곡선이 도출되고 재적표가 작성된 바 있는데, 2007년은 전남 완도지역을 대상으로 약 30본의 입목을 대상으로 조사한 결과이며, 2010년은 278본을 대상으로 조사한 결과를 제시한 것이다(Son et al., 2007; Chung et al., 2010). 기존 재적표(2 종류)와 금번 재적표와의 비교를 위하여 직경 40 cm 내 재적으로 3개 재적표를 비교한 결과 Table 6, Table 7과 같다.

시기별로 작성된 붉가시나무 재적표의 비교하기 위한 분산분석 결과(Table 6), 3개 재적표 집단에서 1% 이상의 유의수준에서 유의성이 인정되어, 시기별(2007년, 2010년, 2023년)로 작성한 재적표 간 일부 재적의 평균값이 차이가 있음을 알 수 있었다.

붉가시나무 임분에서 도출된 시기별 재적표를 상호 비교한 결과(Table 7), 완도지역에서 조사한 자료로 작성한 재적표의 평균값이 가장 높았으며, 제주지역(2010)과 이번(2023)에 조사 분석한 재적표 집단 간은 평균적으로 차이가 없는 것으로 나타탔다. 따라서 분산분석에 따르면 재적표는 크게 두 그룹(2007년 재적표(A)와 2010년⋅2023년 재적표(B))으로 나누어지는 것으로 나타났다. 이런 결과는 2007년 조사된 완도지역에서 조사한 수간고별 붉가시나무 직경 측정 자료가 30여본에 불과하여, 전국 단위의 붉가시나무의 재적 특성을 제대로 반영하지 못하였을 것으로 판단된다. 다만 이 자료도 조사한 완도지역에 한해서 재적 생장은 설명할 수 있을 것이라고 본다.

우리나라에서 생육하고 있는 붉가시나무림의 임목 수간형태를 파악하고자 Max & Burkhart 모형,Lee 모형, Kozak 모형을 후보모형의 추정결과를 비교한 결과 Kozak 모형이 3개 모형 중 최적 모형으로 선정되었다. 현재 우리나라의 난대상록활엽수종 중 조림수종으로 붉가시나무가 가장 대표적인 자원화 수종인데 이에 대한 재적표는 현재 상수리나무 등 낙엽성 참나무류의 재적표를 적용하고 있으나, 직경 수고급에 따른 재적의 차이가 발생하고 있어 본 연구결과로부터 작성된 재적표는 그 활용성이 높다고 할 수 있다. 하지만 본 재적표는 전국의 붉가시나무림을 대상으로 작성한 결과로서, 향후 붉가시나무 재적표 활용에 있어서 생육분포대별 예를 들면, 제주도, 진도, 완도 등의 서남해안 지역별 재적표 활용에 있어서는 지역별 생장특성을 고려할 필요가 있을 것으로 판단된다. 향후 연구에서 상수리나무 등 낙엽성 참나무류, 지역별 붉가시나무림에 대한 재적표에 관한 비교 연구가 추가로 필요할 것으로 판단된다.