서 론
산림에서 벌채되는 입목(立木)은 상업적 용도에 맞춰 목재로 이용되는데, 가지, 잎, 뿌리와 수간(樹幹)의 초두부(梢頭部)를 제외한 목질부가 활용된다(Son et al., 2016). 조재율(造材率)이란 이처럼 판재(板材), 각재(角材) 등 건축이나 가구에 쓰이는 재목(材木), 용재(用材), 펄프재 등으로 이용되는 원목 비율이며, 실제 이용가능한 생산재적과 입목재적의 백분율로 계산된다(National Institute of Forest Science, 2016). 임업 현장에서는 원목 생산량을 알 수 있는 기준으로 사용되는 조재율의 중요성 때문에 정확한 정보를 파악하기 위한 연구가 지속적으로 요구되고 있다(National Institute of Forest Science, 2016).
국내 조재율 연구는 Kim (1963)이 입목의 이용재적에 대해 수행한 것을 시작으로 조재율과 수피율 등 관련 연구가 수행되어 왔다(Kim and Park, 1969; Park and Kim, 1978; Park and Chae, 1979; Woo et al., 1987). 이후 Lee et al. (2000)은 강원지방소나무를 대상으로 수간석해 자료를 활용하여 최소말구직경에 따른 조재율 추정식을 개발하였으며, 해당 모델들과 데이터를 추가하여 Son et al. (2016)은 수간곡선식을 이용하여 수종별 조재율을 새로이 개발하였다. 근래에도 국유림관리소와 임업현장에서 임목(林木) 매각 시 기존의 조재율을 적용하면 이용가능한 재적이 과소추정된다는 지적이 많고, 사업대상지별 공시목을 수집하고 있는 등 조재율의 현실화를 요구하는 사례가 빈번히 발생하여 국립산림과학원에서는 신규 조재율표를 제시하였다(National Institute of Forest Science, 2016).
조재된 생산재(Cut-to-length log)는 지름, 재장 등의 기준으로 구분된 등급에 따라 건축재, 구조재, 내장재, 데크재, 펄프재 등 용도별로 쓰이기 때문에 원목은 등급에 따라 가격의 차이가 크며, 특히 양질의 대경장재는 우수한 등급의 제재목(Sawtimber)으로 분류되어 높은 가격으로 매매되고 있다(Korea Forest Research Institute, 2013; Korea Forestry Promotion Institute, 2024). 기존의 생산재 및 조재율에 관한 연구에서도 이러한 사안을 분석하였지만, 수간곡선식 모델과 원목규격을 이용한 시뮬레이션 결과로 논의되었고 실제 현장에서 벌채·조재되는 생산재 자료를 통한 분석은 이루어지지 않았다(Kwon et al., 2007; Kwon et al., 2013; Son et al., 2016). 이에 따라 생산재 특히 대경장재에 대한 중요성으로 조재율과 재장 수에 대한 연구가 일부 수행되기도 하였다(Lee, I. et al., 2017; Lee et al., 2024).
임업선진국에서는 일찍이 현장자료를 이용한 이용재적 연구가 수행되어 조재율을 예측하고 유형별 이용재적표를 제공해 왔다(Edminster et al., 1980; Honer, 1967; Spurr, 1952; Van Deusen et al., 1981). 입목 초살도를 고려하여 생산재 원목를 예측하는 형수인자를 개발하였고, 등급별 재장 수 및 생산재 재적표를 제공하는 등 실용적인 임업 연구가 활발히 수행되어 왔다(Mesavage and Girard, 1946; Wiant, 1986; Mawson and Conners, 1987; Scrivani, 1989). 특히 원목의 용도별 생산량과 비율이 임업 경제성에 크게 영향을 미침에 따라 개체목과 임분 단위에서 용재와 펄프재 비율을 예측하는 모델이 지속적으로 개발되고 있다(Burkhart et al., 1971; Burkhart and Sprinz, 1984; Burkhart and Bredenkamp, 1989; Keys and McGrath, 2002; Amateis and Burkhart, 2005; Steenberg et al., 2023). 그러나 국내에서는 생산재에 대한 조재율 추정과 관련된 연구결과가 부족한 실정으로 지속적인 연구가 요구되고 있다.
본 연구는 국내 주요 용재수종인 낙엽송(Larix kaempferi (Lamb.) Carrière)을 대상으로 현장에서 매각용으로 벌채·조재한 실증 임목자료를 분석하여 국내 임업에 필요한 생산재 용도별 조재율을 제공하고자 하였다. 이를 위해 목질부 재적이용률과 원목 이용률에 대한 모델을 개발하고, 원료재급 펄프재와 각·판재용 고급 제재목 조재율에 맞춰 용도별로 추정할 수 있는 체계를 마련하고자 하였다.
재료 및 방법
연구자료는 강원도 내 홍천군, 횡성군, 화천군 일원 산림사업지에서 수집된 낙엽송을 대상으로 하였다. 해당 자료는 매각용으로 지름, 재장, 옹이, 할렬, 굽음, 동공 등 기준에 따라 실제 재장길이별로 조재된 생산재라는 특징이 있다. 현장에서 임목은 근원부부터 고급용재로 쓰일 수 있는 3.6 m의 생산재가 최대화될 수 있도록 조재되었으며, 3.6 m의 생산재가 더 이상 조재될 수 없을 때 2.7 m의 생산재로 작업되었다. 단재는 3.6 m, 2.7 m 생산재 조재 후 남은 수간부에서 생산되었으며, 재장 길이는 사업대상지에 따라 2.1 m, 1.8 m로 조재되었다. 해당 재장은 모두 원료재급으로 분류됨에 따라 본 연구에서도 펄프재용 단재로 분석하였다(Korea Forest Research Institute, 2013; Korea Law Information Center, 2023; Korea Forestry Promotion Institute, 2024).
각 임목은 벌도 후 재장별로 조재된 상태에서 측정이 진행되었으며, 1.2 m 높이의 흉고직경을 비롯하여 근주직경 및 생산재 원목별 재장, 원구직경(元口直徑, Butt diameter), 말구직경(末口直徑, Small-end or top diameter)을 측정하였고 초두부(梢頭部, stem cone part)의 길이를 조사하여 개체목의 총수고를 계산하였다(Lee, 2018; Lee et al., 2024). 통나무의 길이인 재장(材長, Log length)은 줄자를 이용하여 측정하였고, 직경은 윤척을 이용하여 수피 내·외 직경 정보를 모두 수집하였다. 모든 직경은 직각 방향으로 각 1회씩 총 2번 측정하였다. 이후 2개의 직경값을 평균하여 최종 직경으로 계산하였다. 수집된 낙엽송은 총 320본이었으며, 흉고직경은 11.2 cm~66.0 cm, 수고는 12.0 m~35.1 m 범위에 분포하고 있었다(Table 1). 그 중 경급 극단에 위치한 크고 작은 입목들은 표본 입목 수가 매우 적어 편향을 야기할 수 있다고 판단하여 모델 개발 시 분석에서 제외하였다. 조재된 생산재는 3.6 m, 2.7 m, 2.1 m, 1.8 m로 고급용재 및 원료재급의 장재와 단재를 모두 포함하고 있었다. 다만, 3.6 m 장재를 최대로 조재하여 경제성을 확보 하였기에 2.7 m 재장이 생산된 입목은 17본으로 적었으며, 대부분 입목에서 3.6m 장재생산이 주를 이루었다. 입목 단위에서 조재된 장재의 말구직경은 수피를 포함하여 최소 7.8 cm 최대 27.8 cm 평균 14.9 cm였으며, 단재의 말구직경은 최소 5.7 cm 최대 15.0 cm 평균 10.1 cm로 다양한 표본 범위를 포함하고 있었다(Table 1).
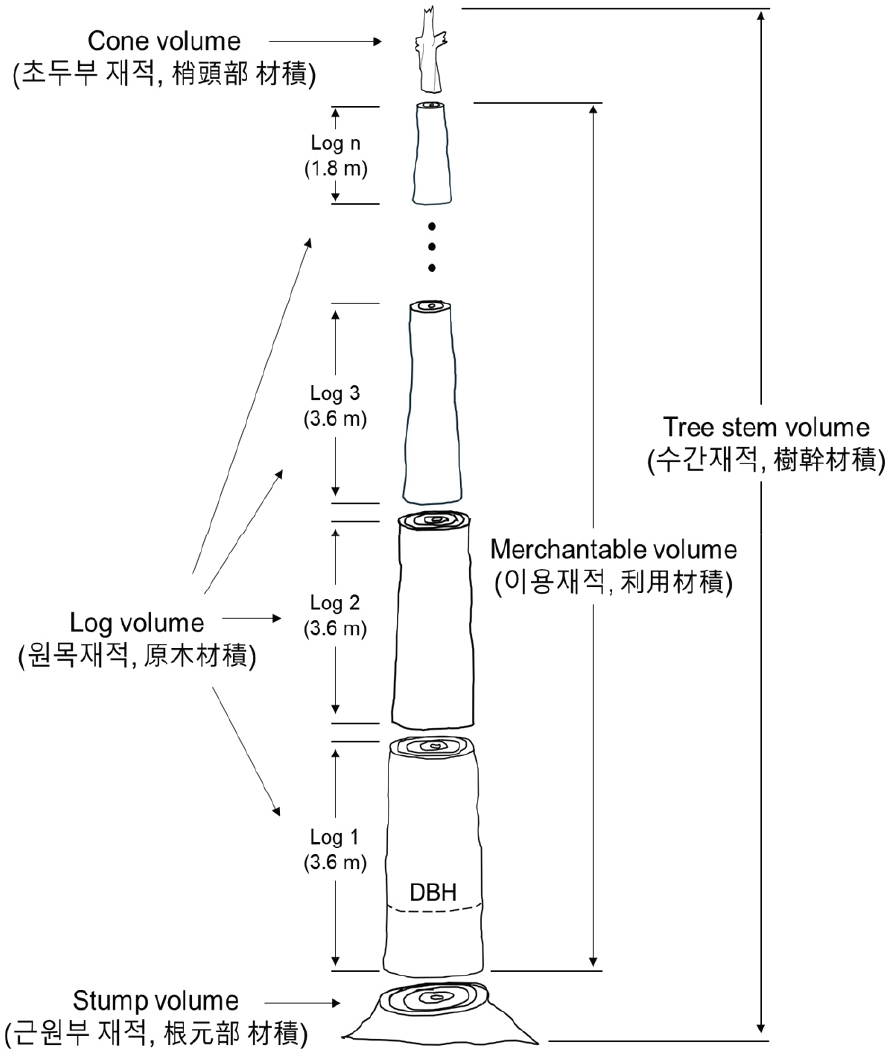
모델 개발 시 필요한 생산재의 재장별 재적(材長材積, Log volume)은 스말리안식(Smalian’s equation)을 이용하였으며, 입목의 총 수간재적(樹幹材積, Tree stem volume)은 지원부(地元部, Ground part)에서 초두부(初頭部, Tip part)까지 재적으로 정의되었으며, 총 생산재적, 원기둥 공식을 통한 근원부 재적(根元部 材積, Stump volume), 원뿔 공식을 통한 초두부 재적(梢頭部 材積, Cone volume)을 더한 값이 입목간재적으로 사용되었다(Lee, I. et al., 2017; Lee, 2018). 본 연구에서 이용재적(利用材積, Merchantable volume) 혹은 생산재적은 근원부와 초두부를 제외한 원목재적(原木材積, Log volume)의 합으로 정의되었다(Figure 1). 조재율(造材率, Bucking rate)은 위 과정을 통해 계산된 수피포함 입목간재적 대비 수피제외 생산재적의 비율로 정의하였다(Son et al., 2016). 목질부 재적이용률(木質部 材積利用率, Xylem volume utilization rate)은 수피포함 수간재적 중 수피제외 수간재적의 비율로, 원목 이용률(原木 利用率, Merchantable log utilization rate)은 수피포함 입목간재적 중 모델에 따라 수피 내·외 생산재적의 비율로 계산하였다.
본 연구에서 개발한 목질부 재적이용률 모델(W model)은 수피포함 흉고직경을 예측변수로 활용하는 식을 이용하였으며, 선행연구를 참고하여 식 1과 식 2의 형태로 모델을 개발하였다(Lee et al., 2000; Son et al., 2016). 본 연구에서는 파라미터 추정의 불안정성을 해결하기 위하여 다항으로 이루어진 선행연구의 유리함수식이 아닌 두 파라미터로 구성된 식 1을 이용하였다. 원목 이용률 모델(M model)은 수피 여부에 따라 개발되었으며, 흉고직경과 입 목 최상단 생산재의 말구직경을 예측변수로 활용한 선행연구를 참고하여 식 3과 식 4의 형태로 모델을 개발하였다(Burkhart, 1977; Son et al., 2016; Lee, D. et al., 2017). 모델 적합을 위해 R 통계소프트웨어(R version 4.3.2)의 nls와 lm 함수를 이용하였다(R core team, 2019).
W: Xylem volume utilization rate with a scale of 0-1 or a ratio of total wood volume to total stem volume,
D: Diameter at breast height (cm) outside bark,
ln(): Natural logarithm of a number inside parenthesis,
M: Merchantable log utilization rate with a scale of 0-1,
exp(): Mathematical constant approximately equal to 2.71828 or Euler’s number with an exponentiation of a number inside parenthesis,
d: Small-end diameter (cm) of the short- or long-length log produced at the highest point of a tree depending on the model type,
a1, a2, a3: Model parameters.
원목 이용률 모델의 경우, 목적에 따른 활용도를 높이기 위하여 장재만을 대상으로 한 모델과 전체 장·단재 생산재를 대상으로 한 모델을 구분하여 개발하였다(식 3과 4). 각 모델의 데이터는 국내 원목 규격 고시를 참고하여 제재용 원목(製材用原木, Sawlog)으로 쓰일 수 있는 재장 3.6 m, 2.7 m 생산재를 장재로, 펄프용(Pulpwood)으로 쓰일 재장 2.1 m, 1.8 m 생산재를 단재로 고려하여 분석을 진행하였다(Korea Law Information Center, 2023; Korea Forestry Promotion Institute, 2024). 개발된 모델들은 실제 관측치 자료의 산점도와 비교하여 적합도를 점검하였다. 특히, 원목 이용률 검증 시 흉고직경과 다양한 말구직경의 크기에 따라 모델 예측값을 산출하여 활용가능성을 평가하였다. 최종적으로 원목 이용률과 목질부 이용률을 복합적으로 활용한 표를 수록하여 전반적인 조재율 범위를 제공하였다.
결과 및 고찰
목질부 재적이용률 모델에는 총 194본의 입목으로부터 수집된 자료가 사용되어 두 가지 모델이 분석되었다(Table 2). 두 모델 모두 파라미터는 유의한 수준으로 추정되었으나, 식 1의 비선형 모델의 통계량이 결정계수(R2) 기준 0.0193 더 높았고, 추정표준오차(Syx) 기준 0.0133 더 낮았다. 특히 W1 모델의 경우 a1 파라미터가 0.9821로 추정되어 해당 이용률까지 점근함을 나타내었는데, 선행연구의 점근선 파라미터 0.9541와 유사한 수준으로 파악되었다(Son et al., 2016).
| Equation | Model | Parameter | Estimate | S.E. | t-value | Pr > |t| | R2 | Syx | n |
|---|---|---|---|---|---|---|---|---|---|
| (1) | W1 | a1 | 0.9821 | 0.0130 | 75.57 | <0.0001 | 0.3030 | 0.0370 | 194 |
| a2 | 2.9549 | 0.3564 | 8.29 | <0.0001 | |||||
| (2) | W2 | a1 | −0.0282 | 0.0125 | −2.25 | 0.0254 | 0.2837 | 0.0437 | 194 |
| a2 | −2.5553 | 0.2930 | −8.72 | <0.0001 |
모델 예측값과 실측값을 비교한 결과, 경급 구간별 큰 편향 없는 목질부 재적이용률이 나타났다(Figure 2). 본 연구의 모델 예측값은 기존에 개발된 Son et al.(2016) 모델에 비해 경급이 작을 때 목질부 이용재적률이 더 낮게 나타났다. Son et al.(2016) 모델은 모든 경급에서 85%~93%을 예측하였고, 본 연구의 모델은 18 cm 이하 소경급에서 5% 이상 더 작은 것으로 나타났다(Figure 2). 그러나 장재 원목이 주로 생산되는 흉고직경 30 cm 이상 구간에서 차이는 2.3% 미만이었고, 40 cm에서는 1.0% 이하로써 경급이 커질수록 예측값의 차이는 미미하였다.
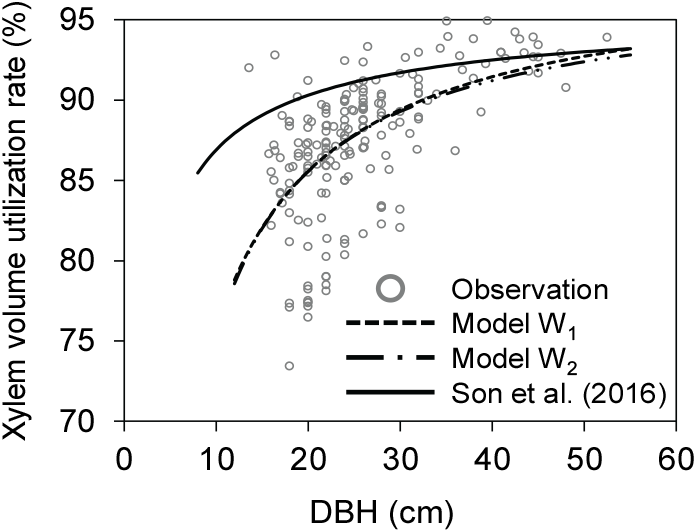
선행연구와의 전반적인 차이는 이용된 임목특성, 모델자료의 경급분포, 재적산출 방법, 모델함수식이 상이하였기 때문이라고 판단된다. 선행연구는 더 넓은 경급 구간을 분석하였고, 수간곡선식을 통해 이용률을 산출한 반면, 본 연구는 현장의 대경재 위주의 생산재를 통해 산출하였다. 선행연구는 전국에서 수집된 표본자료가 많아 전반적인 경향을 대표할 수 있으나, 본 연구와 같이 지역 단위에서는 차이가 확인되었다. 따라서 다양한 지역으로부터 더 많은 임목자료를 수집하여 임분 및 개체목 특성, 재적산출 방법, 모델함수 등을 비교·분석하는 후속 연구가 필요하 다. 다만 현 모델에서도 목질부 이용률은 경급이 작을 때 선행연구와의 차이가 5% 이상 있을 뿐 경급이 클수록 모델 간 차이는 없었다. 즉, 실제 벌채 및 조재되는 생산재의 크기가 대경재급임을 고려하고, 함께 개발된 원목 이용률 모델을 적용하면 현장 이용 시 큰 오차는 없을 것이라 판단된다.
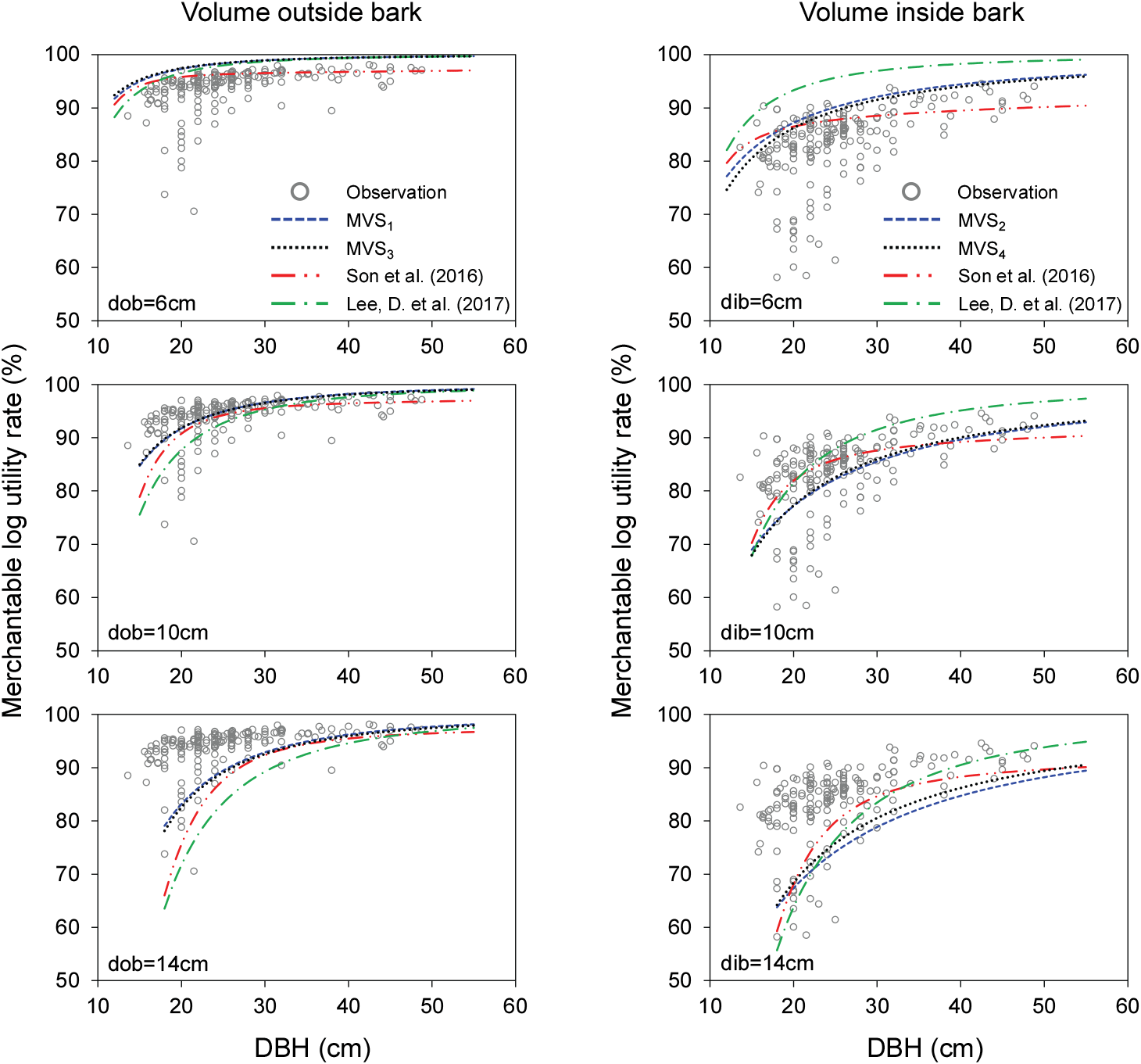
입목으로부터 조재되는 1.8 m~3.6 m의 모든 재장 길이를 대상으로 한 전체 생산재 원목이용률 모델을 제시하였다(Table 3). 모델은 수피포함 이용재적(Merchantable volume for short- and long-logs outside bark, MVS1 and MVS3)과 수피제외 이용재적(Merchantable volume for short- and long-logs inside bark, MVS2 and MVS4)로 구분되며, 각 모델의 예측 변수는 식 3, 4와 같이 흉고직경과 최상단 생산재의 말구직경이다. 이 때 모델 유형에 따라 MVS1와 MVS3에는 수피포함 말구직경이, MVS2와 MVS4에는 수피제외 말구직경이 사용되었다. 식 3을 이용한 모델(MVS1, MVS2)과 식 4를 이용한 모델(MVS3, MVS4) 간의 설명력 차이는 크지 않았으나, 더욱 유의적인 파라미터가 추정된 식 3에 근거한 MVS1과 MVS2를 최종모델로 선정하였다(Table 3). MVS2 모델은 앞서 개발한 목질부 원목 이용률 모델(W1, W2)을 사용하지 않고 바로 수피제외 원목 이용률을 구할 수 있는 특징이 있다. 모델 적합도의 경우, MVS2보다 MVS1에서 결정계수(R2)는 0.5310으로 더 높고 추정표준오차(Syx)는 0.0275로 낮아 MVS1을 활용가능성이 높은 최종 모델로 판단하였다.
| Equation | Type | Model | Parameter | Estimate | S.E. | t-value | Pr > |t| | R2 | Syx | n |
|---|---|---|---|---|---|---|---|---|---|---|
| (3) | dob | MVS1 | a1 | −0.4146 | 0.0450 | −9.22 | <0.0001 | 0.5310 | 0.0275 | 191 |
| a2 | 2.2634 | 0.1512 | 14.97 | <0.0001 | ||||||
| dib | MVS2 | a1 | −0.6161 | 0.0756 | −8.15 | <0.0001 | 0.3462 | 0.0582 | 191 | |
| a2 | 1.2497 | 0.1316 | 9.49 | <0.0001 | ||||||
| (4) | dob | MVS3 | a1 | −0.2519 | 0.1298 | −1.94 | 0.0539 | 0.5372 | 0.0274 | 191 |
| a2 | 2.2633 | 0.1773 | 12.77 | <0.0001 | ||||||
| a3 | 2.1154 | 0.1619 | 13.06 | <0.0001 | ||||||
| dib | MVS4 | a1 | −0.8526 | 0.3224 | −2.64 | 0.0089 | 0.3571 | 0.0577 | 191 | |
| a2 | 0.9794 | 0.1566 | 6.26 | <0.0001 | ||||||
| a3 | 1.1944 | 0.1262 | 9.46 | <0.0001 |
Note: dob is small-end diameter outside bark (cm) of the cut-to-length log produced lastly at the highest point of a tree. dib is small-end diameter inside bark (cm) of the cut-to-length log produced lastly at the highest point of a tree. n is the number of sample trees.
국내 선행연구 중 Lee et al. (2000)은 원목 이용률 모델 개발 시 1변수 모델(흉고직경)과 2변수 모델(흉고직경, 수고)을 비교하였는데, 수고를 이용하더라도 정확성 향상 차이가 크지 않았다고 보고하였다. 이 결과를 반영하여 Son et al.(2016) 연구에서도 흉고직경만을 이용한 원목 이용률을 개발하여 국내 보급되고 있으며(National Institute of Forest Science, 2016), 국외 선행연구에서도 적용되고 있는 상황이다(Honer, 1983; Alegria, 2011). 국내 임업 현장을 고려하면 수고를 사용하지 않은 방법이 측정 변수를 줄이고 자료수집이 간편하여 실용성이 더욱 높다. 따라서, 본 연구에서도 흉고직경과 최상단 생산재 말구직경만을 입력값으로 모델을 개발하여 임업 현장에서도 실질적인 활용이 기대된다.
본 연구의 모델 예측선을 Son et al.(2016) 및 Lee, D. et al.(2017) 모델과 함께 도시하여 비교·분석하였다(Figure 3). 수고 최상단 재장에서 생산되는 말구직경은 작업환경 및 입목특성에 따라 상이할 수 있기 때문에 직경급 6 cm, 10 cm, 14 cm로 구분하여 원목이용률을 도시하였다(Figure 3). 이 때 Son et al.(2016)의 비교값은 모델에 따라 원목이용률 또는 조재율을 활용하였으며, Lee, D. et al.(2017)의 비교값은 수피여부에 따라 개발된 원목이용률을 활용하였다. 분석 결과, 전반적으로 수피여부에 따른 본 모델의 예측값 간 패턴은 유사하였고, 흉고직경이 크고 말구직경이 작을 경우 본 모델이 Son et al.(2016)보다 크게 예측하였다(Figure 3). 한편, 수피제외 원목 이용률의 경우, Lee, D. et al.(2017)의 예측값은 모든 말구직경 범위에서 본 연구보다 높았다. 더 많은 표본 수와 다양한 경급 범위가 고려된 본 연구가 더 정확한 예측값을 제공하고 있다고 판단된다. 본 연구 결과는 Son et al.(2016)의 예측값보다 전반적으로 말구직경에 따른 변화 범위가 더 넓게 나타났다. 대부분의 흉고직경 범위에서 선행연구와 유사한 원목이용률이 나타났으나, 말구직경이 클 경우 다소간 차이가 확인되었다 (Figure 3). 종합적으로 높은 모델 정확도와 선행연구와의 비교 시 예측값을 고려하여 MVS1 모델을 최적모델로 선정하였다.
표본 중 장재가 생산된 입목 총 163본을 대상으로 장재 원목이용률 모델을 개발하였으며, 모델 파라미터는 모두 유의적으로 적합되었다(Table 4). 해당 모델의 데이터는 대부분 3.6 m 장재와 일부 2.7 m 장재로 구성되었으며, 생산재 1.8 m, 2.1 m 단재는 포함되지 않았다. 즉, 장재가 생산된 입목만을 대상으로 원목이용율 모델이 개발되었기 때문에 전체 생산재를 대상으로 한 모델보다 표본 입목 수는 작았다. 이 방법은 수간곡선식을 통한 입목간재적에 의해 산출되는 원목이용률 방법과 데이터 특성 측면에서 차이가 있다(Son et al., 2016). 따라서, 경제성이 높은 각·판재 제제용 원목(Sawlog)의 이용재적을 구할 경우, 본 연구의 장재 원목이용률 모델이 유용하게 비교·검토될 수 있다.
| Equation | Type | Model | Parameter | Estimate | S.E. | t-value | Pr > |t| | R2 | Sy·x | n |
|---|---|---|---|---|---|---|---|---|---|---|
| (3) | dob | MVL1 | a1 | −2.0888 | 0.3247 | −6.43 | <0.0001 | 0.5415 | 0.1388 | 163 |
| a2 | 3.5698 | 0.3310 | 10.78 | <0.0001 | ||||||
| dib | MVL2 | a1 | −1.8658 | 0.2248 | −8.30 | <0.0001 | 0.5412 | 0.1334 | 163 | |
| a2 | 2.6586 | 0.2321 | 11.45 | <0.0001 | ||||||
| (4) | dob | MVL3 | a1 | −6.2078 | 5.2818 | −1.18 | 0.2416 | 0.5471 | 0.1384 | 163 |
| a2 | 2.4365 | 0.2864 | 8.51 | <0.0001 | ||||||
| a3 | 3.0126 | 0.2771 | 10.87 | <0.0001 | ||||||
| dib | MVL4 | a1 | −6.6103 | 3.8999 | −1.69 | 0.0920 | 0.5713 | 0.1293 | 163 | |
| a2 | 1.6314 | 0.1955 | 8.34 | <0.0001 | ||||||
| a3 | 2.2663 | 0.1872 | 12.11 | <0.0001 |
Note: dob is small-end diameter outside bark (cm) of the long-length log produced lastly at the highest point of a tree. dib is small-end diameter inside bark (cm) of the long-length log produced lastly at the highest point of a tree. n is the number of sample trees.
앞선 모델과 같이 장재 원목이용률 모델도 수피포함 이용재적(Merchantable volume for long-logs outside bark, MVL1, MVL3)과 수피제외 이용재적(Merchantable volume for long-logs inside bark, MVL2, MVL4)으로 구분하여 개발하였다. 모델의 예측변수는 식 3, 4와 같으나, 말구직경은 최상단에서 생산된 장재를 대상으로 하였다. 모델 유형에 따라 말구직경은 수피포함(MVL1, MVL3) 값과 수피제외(MVL2, MVL4) 값이 사용되었다. 식 3을 이용한 MVL1, MVL2와 식 4를 이용한 MVL3, MVL4 간의 모델 설명력 차이는 크지 않았으나, 예측정확도가 더 높고 유의적인 파라미터가 추정된 식3에 근거한 MVL1과 MVL2를 최종모델로 선정하였다(Table 4). MVL2 모델은 장재의 수피제외 원목 이용률을 바로 구할 수 있지만, 결정계수도 더 높고 수피가 포함된 상태에서 예측할 수 있는 MVL1 모델이 활용도가 높다고 판단된다(Table 4).
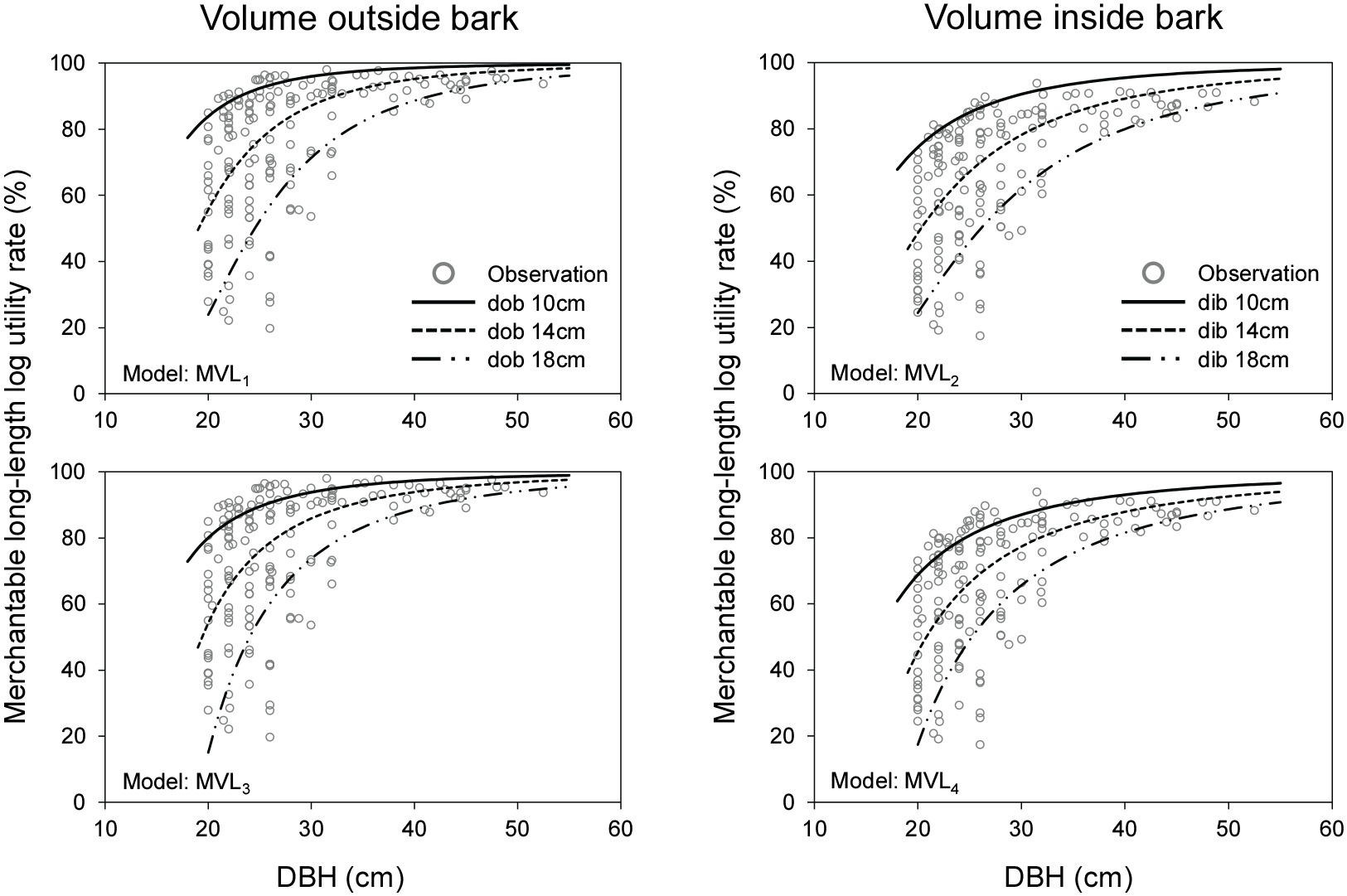
흉고직경 및 말구직경에 따른 예측값을 모델별로 파악하고자, 대경장재의 원목이용률이 말구직경 10 cm, 14 cm, 18 cm를 예시로 사용하여 도시되었다(Figure 4). 흉고직경이 클수록, 말구직경이 작을수록 장재로 이용되는 재장이 길고 재적량이 크기 때문에 장재 원목이용률은 높게 나타났다. 전반적으로 수피포함 모델(MVL1, MVL3)과 수피제외 모델(MVL2, MVL4) 모두 데이터 범위를 잘 포함하며 예측하였다. 각 모델 유형 내 MVL1과 MVL3 차이와 MVL2과 MVL4 차이는 크지 않았다(Figure 4). 분석된 그래프에서 흉고직경이 40 cm 이상 크면서도 원목이용률이 60% 정도로 낮은 표본도 존재하였는데, 이는 해당 입목에서 생산된 장재 원목이용율이 그만큼 낮았던 것으로써 현장 상황에 따라 발생한 표본 간 실질적인 편차가 포함되었음을 의미한다(Figure 4). 전반적으로 개발된 모델 모두 현장의 장재 원목이용률을 적합하게 예측하는 것으로 나타났다.
목질부 재적이용률과 원목 이용률을 적용하여 최종적으로 산출되는 조재율을 흉고직경 및 말구직경에 따라 분석하였다(Figure 5). 본 결과는 장·단재와 장재 조재율 모델에 따라 구분되었고, 각 유형 내 목질부 재적이용률(W1) 적용 유무에 따라 비교되었다. 즉, 모델별 최종 선정된 목질부 재적이용률(W1)과 수피포함 원목 이용률(MVS1, MVL1)의 곱으로 산출되는 조재율(BRS1, BRL1)과 목질부 재적이용률(W1) 계산 없이 바로 산출되는 수피제외 원목 이용률(MVS2, MVL2)을 적용한 조재율(BRS2, BRL2)로 구분하였다(Figure 5). 해당 결과는 선행연구와의 비교를 위해 Son et al.(2016) 및 Lee, D. et al.(2017)의 조재율 모델도 말구직경을 일치시켜 함께 분석하였다.
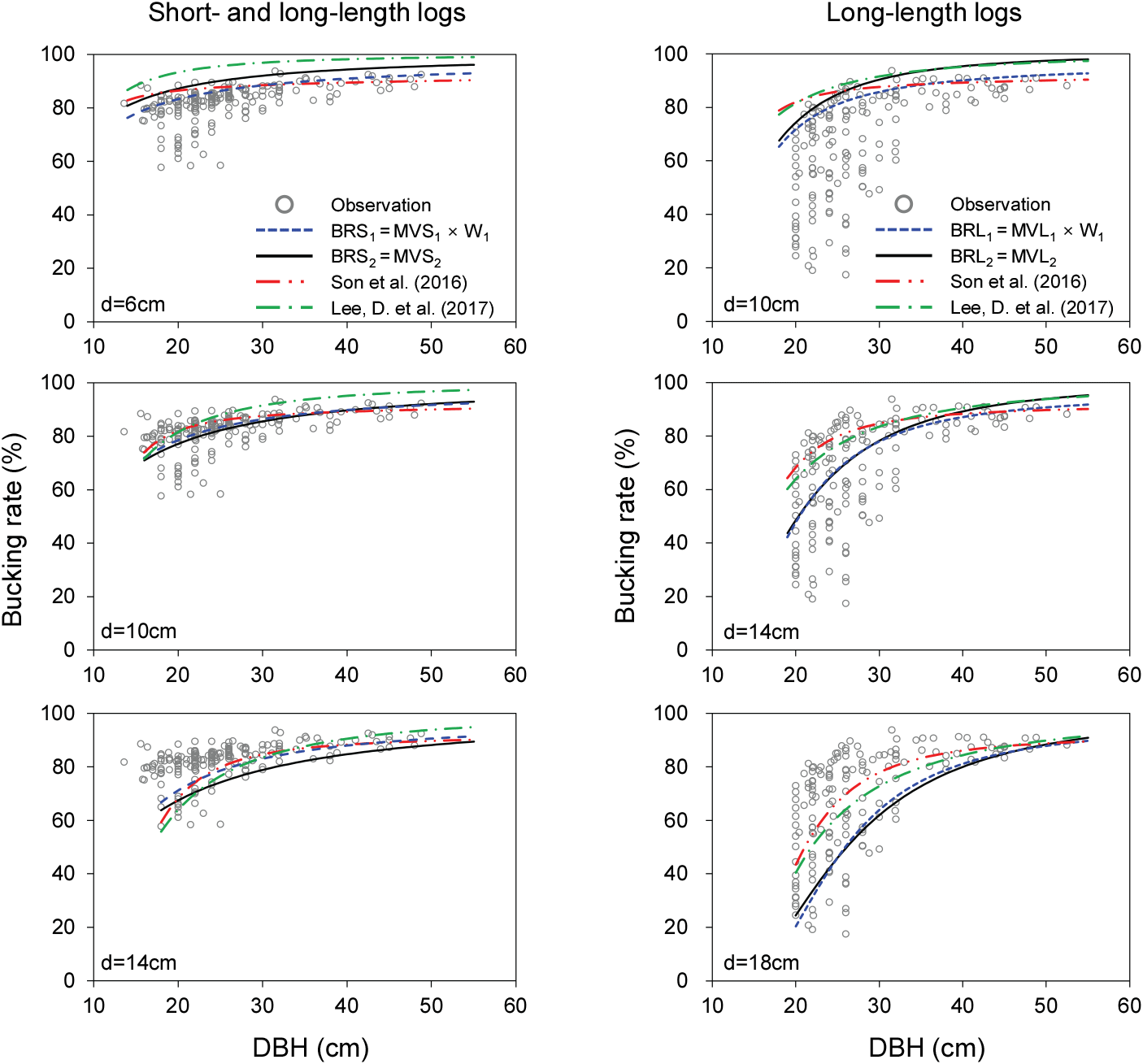
분석 결과 전반적인 조재율 범위는 단재 생산이 포함된 전체 생산재 모델(BRS1, BRS2)에서 장재 모델(BRL1, BRL2)보다 더 높게 나타났다. 흉고직경이 작고, 말구직경이 클수록 조재율은 낮아졌으며, 장재 모델에서 조재율 변화가 더 컸다. 조재율 산출 방법 간 비교 시, BRS1과 BRS2는 말구직경 10 cm에서, BRL1과 BRL2는 말구직경 14cm에서 예측값의 차이가 크지 않았다. 그러나 해당 말구직경 기준보다 크거나 작을 경우, 모델 간 일부 차이가 나타났다. 따라서 앞선 모델 적합도 및 예측 특성을 토대로 BRS1,과 BRL1 방법을 최종 모델로 제시하였다(Tables 3 and 4, Figure 5). 이 방법은 Lee et al. (2000) 및 Son et al. (2016)에서도 검증되어 많은 활용이 기대된다. 선행연구와 비교 결과, Lee, D. et al.(2017) 모델은 본 연구의 장·단재(BRS1) 및 장재(BRL1) 모델보다 모두 높게 예측하였다. 선행연구의 데이터 특성 범위와 표본 수를 고려하면 본 연구의 모델이 더 적합한 것으로 판단된다. Son et al.(2016) 모델은 전체 생산재 모델 BRS2와 유사하였으나, 장재 모델 BRL2와 차이가 있었다. 특히, 흉고직경이 작고, 말구직경이 클수록 모델 예측값의 차이가 뚜렷이 나타났다.
장재 모델에서 같은 말구직경이라도 Son et al.(2016) 및 Lee, D. et al.(2017) 모델보다 본 연구의 조재율이 낮은 이유는 연구목적, 분석방법, 데이터 특성이 다르기 때문이라고 사료된다. 즉, 선행연구는 결함 없는 수간재적의 산출을 목적으로 표본 원판을 균일한 간격 (예: 수고 0.2 m, 1.2 m, 3.2 m, 5.2 m, ... 등)으로 수집하였고, 흉고직경, 수고, 상부수고 등을 활용하여 수간곡선식 혹은 이변수 재적식을 개발하였다. 반면에 본 연구는 실제 생산재 원목 재장에 따라 다양한 길이(1.8 m, 2.1 m, 2.7 m, 3.6 m)로 조재된 원구와 말구를 활용하여 재적 및 조재율을 산출하였다. 더욱이 본 연구자료는 실제 매각되는 생산재임에 따라 여척(餘尺, cross-cut allowance)으로 인한 재적량 차이, 벌채 및 조재 시 파손으로 인한 일부 손실, 형질 등급에 따라 장재로 활용되지 못하는 재장 등 다양한 요인들이 반영되었을 수 있었기 때문에 상대적으로 낮은 장재 조재율이 산출되었다고 판단된다.
국외 임업선진국에서는 밀도와 같은 임분 특성으로 발생하는 상이한 입목 초살도 및 형수를 고려하여 조재율 모델을 유연하게 제공하고 있다(Mesavage and Girard, 1946; Wiant, 1986; Mawson and Conners, 1987; Scrivani, 1989). Son et al.(2016)은 전국 단위 단일화된 모델을 제시하여 임분 특성을 반영하지 않았고, 본 연구는 강원지역의 일부 사업대상지만을 포함하여 추가적인 임분 특성을 반영하지 못 하였다. 따라서, 향후 연구에서는 더 다양한 대상지의 임분 특성을 고려한 많은 표본 수집 및 분석을 통해 조재율 모델이 개발될 필요가 있다.
위 결과를 토대로 최종 선정된 조재율 방법(BRS1, BRL1)을 이용하여 조재율표를 산출하였다. 이 때 조재율표는 전체 생산재를 대상으로 한 Table 5와 장재만을 대상으로 한 Table 6으로 구분하였다. 동일 흉고직경 및 말구직경일 경우, 전반적인 조재율은 전체 생산재 조재율표에서 장재 조재율표보다 다소 높게 나타났다. 이는 고급용재로 쓰이는 장재를 생산하기 위해 더 많은 원목 등급 사항들(예: 굽음, 옹이, 할렬 등)이 고려되어 펄프재로 쓰이는 단재만큼 모든 재적량이 원목 생산으로 이루어지지 못하였기 때문이라 판단된다. 두 조재율표에서 모두 경급이 커질수록, 말구직경이 작을수록 더 높은 조재율이 예측되었다. 제시된 조재율표의 범위 외에도 본 연구에서 개발된 모델에 흉고직경과 말구직경을 예측변수로 입력하면 조재율을 쉽게 산출할 수 있어, 활용이 매우 간편하다. 다만, 본 연구자료의 흉고직경 및 말구직경 범위를 참고하여 과도하게 벗어난 예측변수의 활용은 이용 시 주의가 필요하다. 또한 강원도 일부 사업대상지의 표본을 이용한 모델임에 따라 전국을 대표하거나 모든 임분 특성을 대표하지 않는다. 따라서 지나치게 과밀하거나 과소한 임분의 예측 시 다양한 형수로 인한 오차가 발생할 수 있는 점도 유의가 필요하나, 일반적인 목재생산림의 산림경영 계획 수립 시 큰 편향 없이 예측이 가능할 것이라 기대된다.
결 론
본 연구에서는 낙엽송림 현장의 벌채목 자료를 사용하여 목질부 재적이용률과 원목 이용률 모델을 개발하였다. 특히, 장재만을 대상으로 한 원목 이용률 모델 개발 및 검증은 실제 매매되는 장재 원목 자료를 통해 개발되었으므로 본 연구의 주요 특징이었다. 모델 개발 결과, 입목간재적으로부터 조재율을 바로 산출한 방법(BRS2, BRL2)보다 원목 이용률(MVS1, MVL1)과 목질부 재적이용률(W1)을 곱하여 산출한 조재율(BRS1, BRL1)이 모델 정확성과 예측 범위에서 더 적합한 것으로 분석되었다. 따라서, W1, MVS1, MVL1 모델을 본 연구의 최종 모델로 제시하였다. 해당 모델을 이용하면 흉고직경과 최종 생산재의 말구직경에 따른 실증적인 조재율을 쉽게 구할 수 있다. 본 연구의 전체 생산재 모델과 장재 모델의 예측값은 유사한 흉고직경 및 말구직경에서도 차이가 있었다. 선행연구와 비교 시에도 장재 모델은 조재율 차이가 확인되었다. 용도에 따라 조재율 모델을 적절히 활용한다면 전체 생산재와 고부가가치 대경장재를 예측하여 경제임업을 위한 목재생산림의 산림경영계획 수립에 기여할 수 있을 것이다.
