Journal of Korean Society of Forest Science

Korean Society of Forest Science

J. Korean Soc. For. Sci. 2025; 114(2):121-130

pISSN: 2586-6613, eISSN: 2586-6621

DOI: https://doi.org/10.14578/jkfs.2025.114.2.121

Article

국내 잣나무림의 하층식생 유형별 바이오매스 추정 상대생장식 개발

김다영¹, 신중훈¹, 정형식¹, 한희¹^,²^,^*

Development of Allometric Equations for Biomass Estimation by Understory Vegetation Types in Korean Pine Forests

Dayoung Kim¹, Joonghoon Shin¹, Hyungsik Jeong¹, Hee Han¹^,²^,^*

¹서울대학교 농림생물자원학부

²서울대학교 농업생명과학연구원

¹Department of Agriculture, Forestry and Bioresources, Seoul National University, Seoul 08826, Korea

²Research Institute of Agriculture and Life Sciences, Seoul National University, Seoul 08826, Korea

^*Corresponding Author E-mail: hee.han@snu.ac.kr

© Copyright 2025 Korean Society of Forest Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Feb 05, 2025; Revised: Mar 21, 2025; Accepted: Mar 26, 2025

Published Online: Jun 30, 2025

요 약

본 연구는 국내 잣나무림의 하층식생 유형별 바이오매스를 추정하기 위한 상대생장식을 개발하고자 하였다. 이를 위해 경기도 태화산에 위치한 61년생 잣나무림에서 표본조사를 실시하고, 하층식생을 어린교목과 초본층으로 구분하여 개체 단위 총 바이오매스를 추정하는 회귀모형을 개발하였다. 어린교목에서는 근원직경의 제곱과 식생 높이의 곱이 가장 유효한 독립변수로 도출되었으며(adjusted R² = 0.9506), 초본층에서는 줄기수와 줄기길이를 조합하여 바이오매스를 추정하는 것이 가장 효과적이었다(adjusted R² = 0.7168~0.8580). 반면, 식생 높이를 단독 독립변수로 사용할 경우, 측정의 어려움과 환경적 변동성에 따른 불확실성이 증가하면서 추정력이 낮아지는 경향을 보였다(adjusted R² = −0.0721~0.4392). 또한, 바이오매스 상대생장식에 혼합효과 모형을 적용함으로써 식생 유형별로 개별 모형을 구축하지 않더라도 유형 간 차이를 효과적으로 반영할 수 있음을 확인하였다. 이를 통해 표본 크기에 따른 제약을 완화하는 동시에 바이오매스 추정의 정확성을 향상시킬 수 있었다. 본 연구는 국내 산림의 하층식생 바이오매스 평가를 위한 기초자료를 제공하며, 향후 다양한 임분 형태와 수종을 대상으로 연구를 확장함으로써 산림자원 및 탄소량 평가의 정확성을 제고하는 데 기여할 것으로 기대된다.

Abstract

This study aimed to develop allometric equations to estimate the biomass of understory vegetation by vegetation type in Korean pine forests. A field survey was conducted in a 61-year-old Korean pine forest on Mt. Taehwa in Gyeonggi Province. Understory vegetation was classified as young trees or herbaceous layers, and regression models were developed to estimate the total biomass at the individual plant level for each vegetation type. For young trees, the product of the diameter at the root collar squared and height emerged as the most effective predictor (adjusted R² = 0.9506). For the herbaceous layer, a combination of stem number and stem length provided the most accurate biomass estimates (adjusted R² = 0.7168~0.8580). Conversely, the use of vegetation height alone as an independent variable achieved low estimation performance because of measurement difficulties and environmental influences (adjusted R² = −0.0721~0.4392). Furthermore, the application of mixed-effects models to the biomass allometric equations enabled the integration of differences among vegetation types within a single model. This approach mitigated sample size constraints while improving the accuracy of biomass estimation. This study provides fundamental data for assessing understory biomass in Korean forests, and these findings are expected to help enhance the accuracy of forest resource and carbon stock evaluations by expanding future research to encompass diverse stand structures and tree species.

Keywords: understory vegetation; young trees; herbaceous layer; mixed-effects model; Pinus koraiensis

서 론

산림 바이오매스의 정량화는 산림을 이해하고 평가하는 데 핵심적인 역할을 한다. 산림은 유엔이 인정하는 유일한 탄소흡수원으로, 산림의 탄소저장 및 흡수량 평가가 중요한 과제로 대두되고 있으며, 산림의 주요 탄소저장고인 바이오매스 평가의 중요성 또한 증가하고 있다(Zeng, 2014; Gençay et al., 2018; Saglam et al., 2020). 또한 바이오매스는 산림의 구조 및 생산성을 평가하고 산림생태계 건강을 모니터링하는 지표로도 활용된다. 따라서 지속가능한 산림 관리를 위해 바이오매스의 변화를 정량적으로 평가하고 예측하는 것이 필요하다(Brown, 1997; Oumasst et al., 2024).

기존의 산림 바이오매스 연구는 주로 상층을 구성하는 교목을 대상으로 수행되어 왔다(Brown, 1997; Li et al., 2024). 이는 목재생산이 산림의 주요 기능으로 여겨졌던 과거의 관점에서 비롯된 것으로, 산림의 바이오매스 평가가 경제적 가치가 높고 조사 접근성이 상대적으로 용이한 교목 바이오매스에 초점을 맞추고 있기 때문이다(Mun, 2006; Huff et al., 2017; Deng et al., 2023). 대부분의 바이오매스 추정 모형은 일정 크기 이상의 교목을 대상으로 개발되었으며, 국내에서 공식적으로 사용되는 바이오매스 추정 모형 역시 흉고직경 6 cm 이상의 교목에만 적용되고 있다(Son et al., 2014; Menéndez-Miguélez et al., 2022; NIFoS, 2023).

그러나 교목이 흉고직경 6 cm 이상으로 성장하기까지는 상당한 시간이 소요된다. 국내 현실림 임분수확표에 따르면, 지위지수 10에서 임령 20년일 때 강원지방소나무의 평균 흉고직경은 8.7 cm, 신갈나무는 8.2 cm이며, 속성수로 알려진 백합나무도 지위지수 20에서 흉고직경이 6.2 cm에 도달하기까지 약 5년이 소요된다(NIFoS, 2023). 즉, 임분 내 신규 유입된 치수나 묘목이 바이오매스 조사 대상에 포함되기까지는 약 5~15년의 기간이 요구된다. 어린교목의 생장 속도가 상대적으로 빠르다는 점을 고려할 때, 크기가 작은 교목을 평가에서 제외할 경우 산림 자원량 및 탄소량 변화 평가에서 오차가 발생할 수 있으며, 특히 신규 조림지나 산림복원지에서는 이러한 영향이 더욱 클 것으로 예상된다(Kindermann et al., 2022).

초본층 또한 산림생태계에서 중요한 기능을 수행하지만, 기존의 바이오매스 평가 연구에서는 상대적으로 간과되어 왔다(Yuen et al., 2016). 초본층은 산림생태계의 안정성을 유지하고 야생동물의 서식지와 먹이원을 제공하며, 높은 종 다양성을 기반으로 산림 생물다양성 보전에 기여한다(Gilliam, 2007; Li et al., 2021; Deng et al., 2023). 따라서 산림의 다양한 구조와 기능을 정확하게 이해하고 모니터링하기 위해서는 어린교목 및 초본층을 포함한 하층식생의 바이오매스를 정량적으로 측정할 수 있는 방법론의 개발이 요구된다.

이러한 필요성에 따라 다양한 접근법을 활용하여 하층식생 바이오매스를 정량화하기 위한 시도들이 이루어져 왔다. Annighöfer et al.(2016)은 유럽의 19개 주요 수종을 대상으로 어린교목의 지상부 바이오매스를 개체 단위로 추정하는 상대생장식을 개발하였으며, Istrefi et al.(2019)은 알바니아 천연림에 분포하는 활엽수종 어린교목에 대한 바이오매스 상대생장식을 개발하였다. Daryaei and Sohrabi(2016)과 Puc-Kauil et al.(2020)은 작은 교목의 부위별 및 총 바이오매스를 추정하는 식을 개발하였고, Kenzo et al.(2023)는 말레이시아에서 초본층 식생의 지상부 및 지하부 바이오매스를 추정하는 모형을 제시하였다. 또한, Li et al.(2021), Adhikari et al.(2023), Nobel et al.(2023) 등은 LiDAR를 활용하여 하층식생의 바이오매스 추정 모형을 개발하고 공간적 분포를 지도화하는 등의 연구를 수행하였다.

국내에서도 Mun(2006), Kim et al.(2024)이 생강나무와 개나리, 수수꽃다리 등 일부 관목을 대상으로 바이오매스 추정 모형을 개발하였으나, 연구 대상이 일부 지역이나 수종에 한정되어 있어, 보다 다양한 하층식생에 대한 연구가 필요한 실정이다. 또한 Lee et al.(2023)은 LiDAR 기반 다중회귀모형을 활용하여 하층식생 바이오매스를 추정하였으나, 해당 연구는 식생 자체의 특성보다는 LiDAR 데이터에서 추출된 변수에 의존하여 개체 단위 추정이나 보편적인 적용에는 어려움이 있다.

이에 본 연구는 국내 산림에서 하층식생의 유형별 바이오매스를 정량적으로 평가하기 위해, 식생 특성에 기반한 상대생장식을 개발하는 것을 목표로 하였다. 이를 위해 하층식생을 어린교목과 초본층(초본류, 양치류)으로 구분하고, 경기도 태화산 내 61년생 잣나무림을 대상으로 조사를 수행하였다. 표본조사 및 회귀분석을 통해 하층식생의 다양한 형태적 특성과 바이오매스 간의 관계를 규명하고, 유형별 바이오매스 추정에 적합한 변수 및 회귀모형을 도출하였다. 이후, 개발한 모형을 적용하여 연구대상지 내 하층식생의 바이오매스 및 탄소저장량을 추정하였다.

재료 및 방법

1. 연구대상지

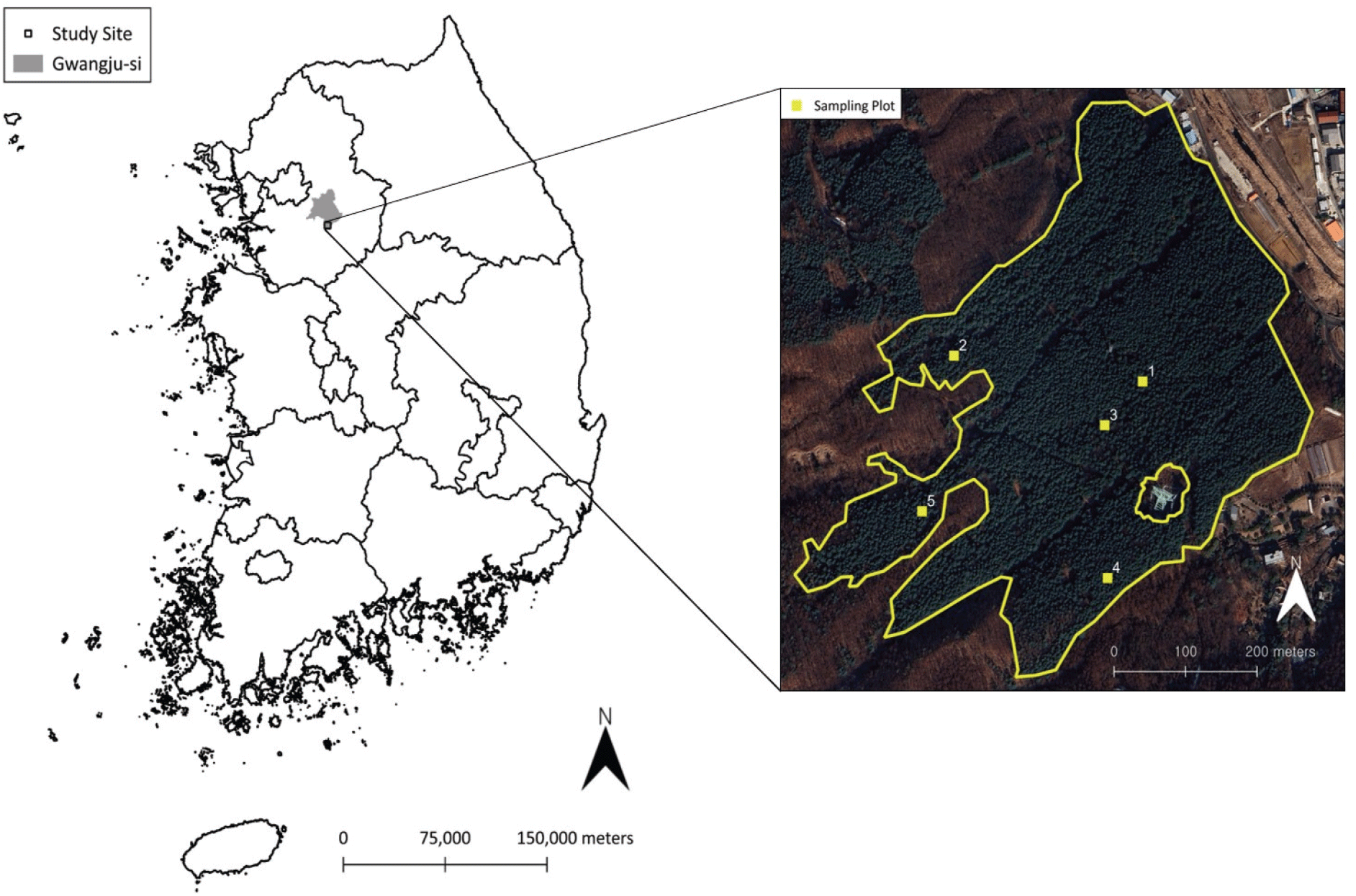
본 연구는 경기도 광주시 도척면 상림리에 위치한 태화산 잣나무림을 대상으로 수행되었다(Figure 1). 해당 임분은 1964년에 조성된 잣나무 조림지로 현재 Ⅶ영급의 동령림을 형성하고 있다. 연구대상지는 동북 사면에 위치하며 평균 경사는 11.5°(4.1~35.6°)이다. 임분 밀도는 580본/ha, 평균 흉고직경은 31.3 cm, 평균 수고는 19.4 m로 조사되었다. 상층은 잣나무가 우점하고 있으며, 하층식생으로는 잣나무 치수, 개옻나무, 쪽동백나무 등이 분포한다. 초본층에는 주름조개풀속과 양치식물이 주를 이루고 있다.

Figure 1. Study site and sampling plots in a Korean pine forest on Mt. Taehwa, Gwangju-si, Gyeonggi-do, Republic of Korea.

Download Original Figure

2. 표본조사

2024년 10월, 하층식생의 형태적 특성을 조사하고 바이오매스 측정용 시료를 채취하기 위해 현장조사를 실시하였다. 조사는 단순임의추출 방식으로 선정된 5개의 표본점에서 수행되었으며(Figure 1), 표본점 선정에는 QGIS의 ‘폴리곤 내부에 랜덤 포인트 생성’ 기능을 활용하였다(QGIS.org, 2024). 각 표본점에는 10 m × 10 m 크기의 교목 조사구와 2 m × 2 m 크기의 어린교목 조사구, 1 m × 1 m 크기의 초본층 조사구가 설치되었으며, 조사구 내 모든 식생을 대상으로 조사가 이루어졌다. 각 식생 유형의 정의 및 조사 항목은 Table 1에 제시되어 있다. 조사된 하층식생은 개체 단위로 채취하였으며, 지상부와 지하부를 포함한 전체 식생을 수집하였다. 채취한 시료는 85°C에서 항량에 도달할 때까지 건조한 후, 0.01 g 단위까지 건중량을 측정하였다.

Table 1. Definitions and measured morphological traits of each understory vegetation group.

Classification	Definition	Morphological trait
Tree	Woody plants with a diameter at breast height of 6 cm or more	Species, Diameter at breast height, Height
Young tree	Woody plants with diameter at breast height of less than 6 cm (or height under 5 m), including saplings and seedlings	Species, Diameter at root collar, Height
Herbaceous layer	Layer of herbaceous plants and ground cover, including grasses, forbs and ferns	Type^a, Number of stems, Length of main stem, Height

The herbaceous plant types were classified into herbs and ferns.

Download Excel Table

3. 하층식생 바이오매스 추정 회귀모형

1) 수종 및 유형에 따른 집단 구분

수집된 하층식생 표본 수는 Table 2와 같으며, 수종 구분이 어려운 표본을 제외한 어린교목 28개, 초본층 91개 표본에 대해 수종 및 유형에 따른 하위집단 구분의 필요성을 평가하였다. 어린교목 집단에서는 일원분산분석(One-way analysis of variance, One-way ANOVA)을 수행하였으며, 초본층 집단에서는 t-검정(t-test)을 통해 초본류와 양치류 집단 간 평균 바이오매스의 통계적 차이를 검토하였다. 두 분석에서 유의수준은 0.05로 설정하였다.

Table 2. Number of understory vegetation samples by species or type.

Classification	Species / Type	Number of samples
Young tree	Pinus koraiensis	13
	Castanea crenata	6
	Fraxinus rhynchophylla	3
	Quercus mongolica	2
	Zanthoxylum schinifolium	2
	Lindera obtusiloba	1
	Prunus sargentii	1
	NA^a	10
Total		38
Herbaceous layer	herbs	76
Herbaceous layer	ferns	15
Total		91

Some samples could not be identified to the species level due to their small size or other limitations.

Download Excel Table

2) 모형 변수

종속변수는 하층식생의 개체별 총 바이오매스로 설정하였으며, 독립변수는 현장조사에서 얻은 식생의 형태적 특성들을 조합하여 사용하였다(Table 3). 여러 가지 변수 조합에 대해 모형을 개발한 후, 각 독립변수에 따른 모형의 성능을 비교하였다.

Table 3. Dependent and independent variables used in biomass allometric equations for understory vegetation.

Classification	Dependent variable	Independent variable
Young tree	Biomass	DRC^a, H^b, DRC·H, DRC²·H
Herbaceous layer	Biomass	Nstem^c, Lstem^d, H, Nstem·Lstem, Nstem·H

DRC: Diameter at root collar

H: Height

Nstem: Number of stems

Lstem: Length of main stem.

Download Excel Table

3) 멱함수 모형(Power function model)

하층식생 바이오매스와 형태적 특성 간의 관계를 설명하기 위해 멱함수 모형을 이용하였다. 멱함수 모형은 전통적으로 바이오매스 상대생장식에 가장 널리 사용되는 회귀모형으로 알려져 있다(Zianis and Mencuccini, 2004; Altanzagas et al., 2019). 멱함수 모형을 이용한 바이오매스 상대생장식 개발 시, 바이오매스 데이터의 이분산성(Heteroscedasticity)을 해결하고 비선형 관계를 선형화하기 위해 종속변수와 독립변수에 로그 변환(Log-log transformation)을 적용할 수 있다(Parresol, 2001; Annighöfer et al., 2016; Manuri et al., 2017). 본 연구는 식 1의 멱함수 모형을 식 2와 같이 로그 변환하여 하층식생의 바이오매스 추정식을 개발하였다.

B i o m a s s = α ⋅ X β ⋅ ϵ

(1)

ln (B i o m a s s) = ln (α) + β ⋅ ln (X) + ln (ϵ)

(2)

Biomass는 하층식생 바이오매스(g)를 의미하며, X는 독립변수, α와 β는 모형 파라미터, ϵ는 잔차항을 의미한다.

로그 변환된 멱함수 모형을 사용할 경우, 실제 종속변수의 값을 구하기 위해서는 원래 단위로의 역변환(Back-transformation) 과정이 필요하다. 이 과정에서 편향(Bias)이 발생하게 되므로 적절한 보정이 필요하며, 이를 위해 본 연구는 식 3과 같이 exp(SEE²/2)를 곱하였다(Baskerville, 1972; Sprugel, 1983; Qin et al., 2020; Adinugroho et al., 2023).

B i o m a s s^u n b i a s e d = B i o m a s s^b i a s e d × exp S E E 2 2

(3)

$B i o m a s s^u n b i a s e d$ 는 보정된 하층식생 바이오매스, $B i o m a s s^b i a s e d$ 는 보정 전 하층식생 바이오매스를 의미하며, SEE는 표준 추정 오차(Standard error of estimate)를 나타낸다.

4) 혼합효과 모형(Mixed-effects model)

선행 결과에서 하위집단 간 유의미한 차이가 존재하는 경우, 하위집단에 의한 변동성을 반영하기 위해 혼합효과 모형을 적용하였다. 혼합효과 모형은 하위집단의 고유한 차이를 통제하면서 전체적인 추세를 분석할 수 있는 통계적 기법으로, 하나의 모형에서 식생 유형이나 지역 특성 등에 따른 차이를 반영할 수 있다(Meng et al., 2007; Feng et al., 2021). 혼합효과 모형에서 고정효과(Fixed effects)는 모든 관측치에 공통적으로 적용되는 변수 간의 관계를 설명하며, 임의효과(Random effects)는 하위집단별로 발생하는 차이를 설명한다.

본 연구는 식 4와 같이 형태적 특성에 의한 고정효과와 식생 유형에 의한 임의효과를 반영하여 하층식생의 바이오매스를 추정하는 혼합효과 모형을 구성하였다.

B i o m a s s = α + β ⋅ X + u i + ϵ

(4)

Biomass는 하층식생의 바이오매스(g), X는 독립변수를 의미한다. α와 β 는 고정효과를 설명하는 파라미터, u_i는 식생 유형(i)에 따른 임의효과, ϵ는 잔차항을 나타낸다.

4. 모형 평가 및 검증

독립변수와 모형 종류에 따른 회귀모형의 바이오매스 추정력을 평가 및 비교하기 위해 조정된 결정계수(Adjusted R-square, Adjusted R²), 평균제곱근오차(Root mean squared error, RMSE), 평균편향오차(Mean bias error, MBE)를 이용하였다(식 5,6,7).

A d j u s t e d R 2 = 1 − 1 − R 2 (n − 1) n − k − 1

(5)

R M S E = 1 n ∑ i = 1 n y i − y i^2

(6)

M B E = 1 n ∑ i = 1 n y i^− y i

(7)

R²는 결정계수, n은 관측치의 수, k는 독립변수의 수이며, y_i는 관측값, $y i^$ 은 모형의 예측값을 의미한다.

세 가지 기준에 따라 유형별 최종 모형을 선정한 후, Leave-one-out cross-validation(LOOCV)를 통해 검증하였다. LOOCV는 n개의 데이터 중 하나의 데이터를 검증 데이터로 사용하고, 나머지 n-1개의 데이터를 학습 데이터로 활용하여 모형 개발 및 검증 과정을 n번 반복한다. LOOCV는 표본 수가 적을 때 효과적인 검증 기법으로 알려져 있으며(Yadav and Sanyam, 2016), 본 연구는 LOOCV를 수행한 후 평균 RMSE를 계산하였다. 본 연구와 관련된 모든 통계분석은 R version 4.4.1을 이용하여 수행하였다.

5. 하층식생 바이오매스 및 탄소저장량 추정

개발한 하층식생 바이오매스 상대생장식을 적용하여 연구대상지의 하층식생 바이오매스를 추정하고, 교목 바이오매스와 비교하였다. 하층식생 바이오매스는 선정된 모형에 표본조사 자료를 적용하여 단위면적(ha) 당 평균 바이오매스를 계산하였다. 교목 바이오매스는 흉고직경과 수고 조사 자료를 바탕으로 임분수확표(NIFoS, 2023) 및 바이오매스 상대생장식(NIFoS, 2014)을 이용하여 산출하였다. 탄소저장량 계산을 위한 탄소함량비는 0.5를 적용하였다.

결 과

1. 수종 및 유형에 따른 차이

One-way ANOVA 분석 결과, 어린교목 집단에서 수종에 따른 평균 바이오매스의 차이는 통계적으로 유의하지 않은 것으로 나타났다(p=0.96). 반면, 초본층 집단에서는 t-검정을 통해 초본류와 양치류 집단 간 평균 바이오매스의 차이가 통계적으로 유의미한 것으로 확인되었다(p<0.005). 이에 따라 초본류와 양치류를 구분하여 별도의 멱함수 모형 상대생장식을 개발하였다. 동시에 혼합효과 모형을 활용하여 유형(초본류, 양치류)별 임의효과를 포함하는 초본층 상대생장식을 개발하였다.

2. 어린교목의 바이오매스 상대생장식

멱함수 모형을 이용하여 어린교목의 바이오매스 상대생장식을 개발한 결과는 Table 4와 같다. 근원직경의 제곱과 식생 높이의 곱(DRC²·H)을 독립변수로 하는 모형에서 Adjusted R²가 0.9506으로 가장 높게 나타났으며, RMSE (68.1624)와 MBE(16.8551)도 낮은 값을 보였다. 해당 모형에 역변환 보정계수를 적용하면 어린교목의 바이오매스 상대생장식은 식 8과 같이 표현할 수 있다. 선정된 모형에 대해 LOOCV를 수행한 결과, RMSE는 35.1385로 계산되었다.

B i o m a s s^= 1.2131 ⋅ D R C 2 ⋅ H 0.7651 ⋅ 2.2317

(8)

Table 4. Parameters, standard errors, and performance metrics of biomass allometric equations based on the power function model for the young tree group by independent variables.

Independent variable	Parameters			SEE^a	Adjusted R²	RMSE^b	MBE^c
Independent variable	α	β₁	β₂	SEE^a	Adjusted R²	RMSE^b	MBE^c
DRC^d	28.1402	2.0293	-	1.5210	0.8935	100.0943	3.6273
H^e	0.0011	2.3236	-	1.5060	0.1898	276.0763	84.3704
DRCㆍH	0.1966	1.1910	-	1.2100	0.9047	94.6881	29.4355
DRC²ㆍH	1.2131	0.7651	-	1.2670	0.9506	68.1624	16.8551
DRC, H	0.1256	1.1019	1.2940	1.2240	0.8645	111.3303	36.4808

SEE: Standard error of estimate

RMSE: Root mean squared error

MBE: Mean bias error

DRC: Diameter at root collar

H: Height.

Download Excel Table

$B i o m a s s^$ 는 바이오매스 추정값, DRC는 근원직경, H는 식생 높이를 의미한다.

3. 초본층의 바이오매스 상대생장식

1) 초본류 멱함수 모형

초본류 바이오매스를 추정하는 멱함수 모형의 매개변수 및 추정 성능은 Table 5에 제시되어 있다. 줄기수와 줄기길이의 곱(Nstem·Lstem)을 독립변수로 할 때 Adjusted R²(0.7168)가 가장 높고 RMSE(0.1936)가 가장 낮았다. 해당 모형에 의한 초본류의 바이오매스 상대생장식은 식 9에 제시되었으며, LOOCV 분석 결과 평균 RMSE는 0.1188로 나타났다.

B i o m a s s^= 0.0092 ⋅ (N s t e m ⋅ L s t e m) 0.8711 ⋅ 1.2257

(9)

Table 5. Parameters, standard errors, and performance metrics of biomass allometric equations based on the power function model for the herb group by independent variables.

Independent variable	Parameters			SEE^a	Adjusted R²	RMSE^b	MBE^c
Independent variable	α	β₁	β₂	SEE^a	Adjusted R²	RMSE^b	MBE^c
Nstem^d	0.0882	1.2956	-	0.9027	0.3805	0.2863	0.0033
Lstem^e	0.0074	1.0656	-	0.7498	0.4535	0.2689	−0.0160
H^f	0.0283	0.7572	-	0.8813	0.2394	0.3172	−0.0173
NstemㆍLstem	0.0092	0.8711	-	0.6380	0.7168	0.1936	−0.0062
NstemㆍH	0.0255	0.6866	-	0.7751	0.4807	0.2621	−0.0148
Nstem, Lstem	0.0090	0.8439	0.8853	0.6422	0.7124	0.1937	−0.0061
Nstem, H	0.0292	0.9444	0.5778	0.7692	0.5174	0.2510	−0.0077

SEE: Standard error of estimate

RMSE: Root mean squared error

MBE: Mean bias error

Nstem: Number of stems

Lstem: Length of main stem

H: Height.

Download Excel Table

$B i o m a s s^$ 는 바이오매스 추정값, Nstem은 줄기수, Lstem은 줄기길이를 의미한다.

2) 양치류 멱함수 모형

Table 6은 양치류의 바이오매스를 추정하는 멱함수 모형의 매개변수 및 추정 성능을 보여준다. 줄기수(Nstem)와 줄기길이(Lstem)를 독립변수로 사용하는 모형에서 추정력이 가장 뛰어난 것으로 나타났다(Adjusted R²=0.7487, RMSE=4.8521, MBE=0.4955). 두 변수를 독립변수로 하는 양치류의 바이오매스 상대생장식은 식 10과 같으며, 교차검증 시 RMSE는 4.2582로 나타났다.

B i o m a s s^= 0.0019 ⋅ (N s t e m) 0.5177 ⋅ (L s t e m) 2.0404 ⋅ 1.1630

(10)

Table 6. Parameters, standard errors, and performance metrics of biomass allometric equations based on the power function model for the fern group by independent variables.

Independent variable	Parameters			SEE^a	Adjusted R²	RMSE^b	MBE^c
Independent variable	α	β₁	β₂	SEE^a	Adjusted R²	RMSE^b	MBE^c
Nstem^d	2.3453	0.5762	-	1.2350	0.4195	7.6755	3.8132
Lstem^e	0.0037	2.0825	-	0.7115	0.3475	8.1375	−0.2441
H^f	0.4815	0.8695	-	1.0920	−0.0721	10.4313	2.5942
NstemㆍLstem	0.0517	0.9297	-	0.8780	0.5364	6.8597	3.2699
NstemㆍH	0.4593	0.5753	-	1.0570	0.4898	7.1961	2.9820
Nstem, Lstem	0.0019	0.5177	2.0404	0.5496	0.7487	4.8521	0.4955
Nstem, H	0.3526	0.3872	0.7702	1.0780	0.2391	8.4430	3.1802

SEE: Standard error of estimate

RMSE: Root mean squared error

MBE: Mean bias error

Nstem: Number of stems

Lstem: Length of main stem

H: Height.

Download Excel Table

$B i o m a s s^$ 는 바이오매스 추정값, Nstem은 줄기수, Lstem은 줄기길이를 의미한다.

3) 초본층 혼합효과 모형

t-검정을 통해 하위집단 간 바이오매스의 차이가 확인된 초본층에 대해 혼합효과 모형을 적용하여 바이오매스를 추정한 결과는 Table 7과 같다. 줄기수와 줄기길이의 곱(Nstem·Lstem)을 독립변수로 사용하는 모형에서 Adjusted R²가 0.8580으로 가장 높았고, RMSE는 2.0838, MBE는 5.7292e-16으로 낮게 나타났다. 해당 모형은 식 11을 통해 나타낼 수 있으며, LOOCV 결과 평균 RMSE 1.1755로 산출되었다. 식 11에서 임의효과 항(u_i)은 식생 유형마다 달라지는 고정효과의 변동을 반영하며, 해당 항의 표준편차는 2.0019이다.

B i o m a s s^= 0.4868 + 0.0300 ⋅ (N s t e m ⋅ L s t e m) + u i

(11)

Table 7. Fixed and random effects, and performance metrics of biomass allometric equations based on the mixed-effects model for the herbaceous layer by independent variables.

Independent variable	Fixed effects			Random effects^a	Adjusted R²	RMSE^b	MBE^c
Independent variable	α	β₁	β₂	Random effects^a	Adjusted R²	RMSE^b	MBE^c
Nstem^d	−0.7003	1.3855	-	1.9419	0.7676	2.6661	9.90e-16
Lstem^e	2.7093	0.0808	-	5.8357	0.4432	4.1267	−1.87e-16
H^f	3.0963	0.1168	-	5.8983	0.4392	4.1414	2.79e-15
NstemㆍLstem	0.4868	0.0300	-	2.0019	0.8580	2.0838	5.73e-16
NstemㆍH	0.6561	0.0483	-	2.0615	0.7766	2.6139	−1.04e-16
Nstem, Lstem	−1.2553	1.3575	0.0231	1.7745	0.7674	2.6520	−6.12e-17
Nstem, H	−1.1516	1.3609	0.0331	1.7839	0.7671	2.6539	1.14e-15

Random effects: Standard deviation of random intercept

RMSE: Root mean squared error

MBE: Mean bias error

Nstem: Number of stems

Lstem: Length of main stem

H: Height.

Download Excel Table

$B i o m a s s^$ 는 바이오매스 추정값, Nstem은 줄기수, Lstem은 줄기길이를 의미하며, u_i는 임의효과 항을 나타낸다.

4. 하층식생 바이오매스 및 탄소저장량

어린교목과 초본층의 표본조사 자료를 각각 식 8과 식 11에 적용한 결과, 연구대상지 내 하층식생의 바이오매스량은 어린교목 2.7946 t/ha, 초본층 0.3378 t/ha로 계산되었다. 한편, 교목의 바이오매스량는 448.4417 t/ha로, 임분 내 하층식생 바이오매스가 차지하는 비율은 0.7%로 나타났다. 탄소함량비 0.5를 적용할 경우, 하층식생의 탄소저장량은 1.5662 tC/ha로, 연구대상지 전체에서 하층식생에 저장된 탄소량은 43.0710 tC/ha에 이르는 것으로 분석되었다.

고 찰

태화산 잣나무림에서 어린교목과 초본층(초본류, 양치류)에 대한 바이오매스 상대생장식을 개발한 결과, 독립변수와 회귀모형 종류에 따라 모형의 추정력이 달라지는 것을 확인하였다. 어린교목의 경우, 근원직경과 식생 높이를 조합하여 독립변수로 사용할 때, 각 변수를 단독으로 사용하는 경우보다 더 높은 추정력을 보였다. Antonio et al.(2007), Hosoda and Iehara(2010) 등의 연구에서도 나타난 바와 같이, 바이오매스를 추정할 때 직경 변수만을 이용하는 것보다 직경과 높이 변수를 결합하여 사용하는 것이 더 효과적이었다. 유럽에서 근원직경과 식생 높이를 이용하여 어린나무의 바이오매스를 추정한 Annighöfer et al.(2016)의 연구에서도 근원직경의 제곱과 식생 높이의 곱을 예측변수로 활용했을 때 예측 정확도가 가장 높았으며, 본 연구에서는 그러한 경향이 더욱 뚜렷하게 나타났다.

반면, 식생 높이만을 단독 독립변수로 사용하는 경우, 어린교목과 초본층 모두에서 모형의 추정력이 낮게 나타났다. 이는 Istrefi et al.(2019)의 연구 결과와 일치하며, 하층식생 높이의 정확한 측정이 어렵고 환경적 요인에 의한 변동성이 크기 때문으로 해석된다. 작은 크기와 연약한 특성을 지닌 하층식생은 토양 조건이나 바람 등의 환경적 요인에 의해 줄기가 기울거나 휘어지기 쉬우며, 이는 식생 높이의 변동성과 측정 오차를 초래한다(Pérez-Harguindeguy et al., 2013). 따라서 복잡한 하층식생 환경에서는 정확한 현장 측정이 가능한 변수를 선택하는 것이 바이오매스 상대생장 예측에 영향을 미칠 수 있다.

초본층의 바이오매스 추정 모형에서는 줄기수와 줄기길이를 함께 사용하여 바이오매스를 추정하는 것이 가장 효과적이었다. 독립변수에 식생 높이가 포함된 경우보다 줄기길이를 포함했을 때 모형의 성능이 다소 향상되었으나, 그 차이는 크지 않았다. 식생 높이와 마찬가지로 줄기길이가 단독으로 독립변수로 사용된 경우, 모형의 추정력이 낮게 나타났다. 이러한 결과는 LiDAR 등을 활용하여 하층식생의 수직적 특성을 보다 정확히 측정하고 이를 바이오매스 추정에 활용하기 위한 추가 연구의 필요성을 시사한다.

혼합효과 모형을 활용하여 초본류와 양치류를 포함한 초본층 바이오매스를 추정한 결과, 멱함수 모형을 이용하여 두 집단을 별도로 추정한 경우보다 추정 성능이 유의미하게 향상되었으며 예측 편향이 감소하였다. 혼합효과 모형에서 초본층 하위집단(초본류, 양치류)에 의한 차이를 임의효과로 간주함으로써 집단 간 고유한 변동성을 반영할 수 있었다. 이는 작은 표본 크기에서 발생할 수 있는 제약을 완화하며 바이오매스 추정의 정확도를 높이는 데 기여하였다(Chen et al., 2012; Abreu et al., 2020). 이를 통해 제한된 표본에서 하위집단을 구분하여 모형을 설계하는 대신 혼합효과 모형을 활용하면 보다 효율적인 추정이 가능함을 확인하였다.

한편, 개발한 상대생장식을 적용하여 연구대상지의 하층식생 바이오매스 및 탄소저장량을 추정한 결과, 임분 내 하층식생 바이오매스가 차지하는 비율이 0.7%로 낮게 나타났다. 이는 본 연구의 대상지가 임분 밀도가 높고 성숙한 Ⅶ영급 잣나무 조림지로, 하층식생 비율이 상대적으로 낮은 환경적 특성을 갖기 때문인 것으로 판단된다. 산림 바이오매스 및 탄소저장에서 상층 및 하층식생의 기여도는 임분 유형과 임령에 따라 달라질 수 있으며(Van Den Bor et al., 2024), 일반적으로 어린 임분에서 하층식생의 비율이 더 높은 경향을 보인다(Rue-Johns et al., 2021; Kindermann et al., 2022). 따라서, 향후 다양한 임분 유형과 임령, 수종 등에 대한 하층식생 바이오매스 상대생장식을 개발하고, 환경 요인에 따른 하층식생 발달 경향을 비교하는 연구가 필요할 것으로 판단된다.

결 론

본 연구는 하층식생을 어린교목과 초본층, 초본류와 양치류로 유형화하여 바이오매스 추정 상대생장식을 개발하였다. 연구 결과를 통해 식생 유형별 형태적 특성과 바이오매스 간의 관계를 규명하였으며, 혼합효과 모형의 유효성을 검증하였다. 또한 LiDAR와 같은 첨단 측정 기술의 활용이 현장조사와 추정의 정확성을 향상시킬 수 있음을 제안하였다. 혼합효과 모형을 활용한 분석은 하나의 모형 내에서 식생 유형 간 차이를 반영할 수 있어, 제한된 표본에서 바이오매스 추정의 정확도를 향상시키는 데 효과적임을 입증하였다.

한편 본 연구는 Ⅶ영급 잣나무 조림지에서 수집한 제한된 표본을 기반으로 수행되었다는 한계가 있다. 향후 다양한 임분 형태와 수종에 대한 하층식생 바이오매스 추정식의 개발이 필요하며, 혼합효과 모형의 활용은 이러한 연구의 효율성을 높이는 데 기여할 것으로 기대된다. 하층식생을 포함한 산림 바이오매스 평가는 산림 자원량 및 탄소량 평가의 신뢰성을 강화할 뿐만 아니라, 산림생태계의 구조와 기능을 보다 정확히 이해하는 데 중요한 기초 자료를 제공할 것이다.

감사의 글

본 연구는 산림청(한국임업진흥원) ‘산림과학기술 연구개발사업(RS-2024-00400603)’의 지원에 의하여 이루어진 것입니다.

References

Abreu, J.C., da Silva, J.A.A., Ferreira, R.L.C., Soares, C.P.B., Torres, C.M.M.E., Farias, A.A. and Tavares Junior, I.D.S. 2020. Mixed models for biomass prediction in the semiarid zone of Pernambuco State, Brazil. Scientia Forestalis 45(128): e3246.

Adhikari, A., Peduzzi, A., Montes, C.R., Osborne, N. and Mishra, D.R. 2023. Assessment of understory vegetation in a plantation forest of the southeastern United States using terrestrial laser scanning. Ecological Informatics 77: 102254.

Adinugroho, W.C., Krisnawati, H., Imanuddin, R., Siregar, C.A., Weston, C.J. and Volkova, L. 2023. Developing biomass allometric equations for small trees in mixed-species forests of tropical rainforest ecozone. Trees, Forests and People 13: 100425.

Altanzagas, B., Luo, Y., Altansukh, B., Dorjsuren, C., Fang, J. and Hu, H. 2019. Allometric equations for estimating the above-ground biomass of five forest tree species in Khangai, Mongolia. Forests 10(8): 661.

Annighöfer, P. et al. 2016. Species-specific and generic biomass equations for seedlings and saplings of European tree species. European Journal of Forest Research 135: 313-329.

Antonio, N., Tomé, M., Soares, P. and Fontes, L. 2007. Effect of tree, stand, and site variables on the allometry of Eucalyptus globulus tree biomass. Canadian Journal of Forest Research 37(5): 895-906.

Baskerville, G.L. 1972. Use of logarithmic regression in the estimation of plant biomass. Canadian Journal of Forest Research 2(1): 49-53.

Brown, S. 1997. Estimating biomass and biomass change of tropical forests: a primer. FAO Forestry Paper 134. Rome, Italy.

Chen, Q., Laurin, G.V., Battles, J.J. and Saah, D. 2012. Integration of airborne lidar and vegetation types derived from aerial photography for mapping aboveground live biomass. Remote Sensing of Environment 121: 108-117.

10.

Daryaei, A. and Sohrabi, H. 2016. Additive biomass equations for small diameter trees of temperate mixed deciduous forests. Scandinavian Journal of Forest Research 31(4): 394-398.

11.

Deng, J. et al. 2023. Forest understory vegetation study: current status and future trends. Forestry Research 3: 6.

12.

Feng, H., Chen, Q., Hu, Y., Du, Z., Lin, G., Wang, C. and Huang, Y. 2021. Estimation of forest aboveground biomass by using mixed-effects model. International Journal of Remote Sensing 42(22): 8675-8690.

13.

Gençay, G., Birben, Ü. and Durkaya, B. 2018. Effects of legal regulations on land use change: 2/B applications in Turkish forest law. Journal of Sustainable Forestry 37(8): 804-819.

14.

Gilliam, F.S. 2007. The ecological significance of the herbaceous layer in temperate forest ecosystems. BioScience 57(10): 845-858.

15.

Hosoda, K. and Iehara, T. 2010. Aboveground biomass equations for individual trees of Cryptomeria japonica, Chamaecyparis obtusa and Larix kaempferi in Japan. Journal of Forest Research 15(5): 299-306.

16.

Huff, S., Ritchie, M. and Temesgen, H. 2017. Allometric equations for estimating aboveground biomass for common shrubs in northeastern California. Forest Ecology and Management 398: 48-63.

17.

Istrefi, E., Toromani, E., Collaku, N. and Thaci, B. 2019. Allometric biomass equations for young trees of four broadleaved species in Albania. New Zealand Journal of Forestry Science 49.

18.

Kenzo, T., Yoneda, R. and Alias, M.A. 2023. Estimation of above and belowground biomass for grass, herb, and fern species in Peninsula Malaysia. Tropical Ecology 64(3): 500-510.

19.

Kim, H. et al. 2024. Development of Allometric Equations for Carbon Storage Analysis of Shrubs in Settlement - Forsythia koreana and Syringa oblata var. dilatata in Sejong-si. Journal of Environmental Impact Assess 33(6): 422-430.

20.

Kindermann, L., Dobler, M., Niedeggen, D. and Linstädter, A. 2022. A new protocol for estimation of woody aboveground biomass in disturbance-prone ecosystems. Ecological Indicators 135: 108466.

21.

Lee, H., Kim, S. and Choe, H. 2023. Backpack-and UAV-based Laser Scanning Application for Estimating Overstory and Understory Biomass of Forest Stands. Journal of Korean Society of Forest Science 112(3): 363-373.

22.

Li, S., Wang, T., Hou, Z., Gong, Y., Feng, L. and Ge, J. 2021. Harnessing terrestrial laser scanning to predict understory biomass in temperate mixed forests. Ecological Indicators 121: 107011.

23.

Li, Y., Hu, R., Xing, Y., Pang, Z., Chen, Z. and Niu, H. 2024. Comparison of three approaches for estimating understory biomass in Yanshan Mountains. Remote Sensing 16(6): 1060.

24.

Manuri, S. et al. 2017. Effect of species grouping and site variables on aboveground biomass models for lowland tropical forests of the Indo-Malay region. Annals of Forest Science 74: 23.

25.

Menéndez-Miguélez, M., Calama, R., Del Río, M., Madrigal, G., López-Senespleda, E., Pardos, M. and Ruiz-Peinado, R. 2022. Species-specific and generalized biomass models for estimating carbon stocks of young reforestations. Biomass and Bioenergy 161: 106453.

26.

Meng, Q., Cieszewski, C.J., Madden, M. and Borders, B. 2007. A linear mixed-effects model of biomass and volume of trees using landsat ETM+ images. Forest Ecology and Management 244(1-3): 93-101.

27.

Mun, H.T. 2006. Biomass Estimation of Shrub Lindera obtusiloba by Allometry. Journal of Ecology and Environment 29(5): 485-488.

28.

NIFoS (National Institute of Forest Science). 2014. Carbon emission factors and biomass allometric equations by species in Korea. NIFoS. Seoul, Republic of Korea. pp. 97.

29.

NIFoS (National Institute of Forest Science). 2023. The table of the stem volume, biomass, and yield. NIFoS. Seoul, Republic of Korea. pp. 377.

30.

Nobel, J.S., Rijsdijk, K.F., Cornelissen, P. and Seijmonsbergen, A.C. 2023. Towards prediction and mapping of grassland aboveground biomass using handheld LiDAR. Remote Sensing 15(7): 1754.

31.

Oumasst, A., Tiouidji, F.E., Tabi, S., Zahidi, A., El Mousadik, A., El Finti, A., Aitlhaj, A. and Hallam, J. 2024. Development of allometric equations to determine the biomass of plant components and the total storage of carbon dioxide in young mediterranean argan trees. Sustainability 16(11): 4592.

32.

Parresol, B.R. 2001. Additivity of nonlinear biomass equations. Canadian Journal of Forest Research 31(5): 865-878.

33.

Pérez-Harguindeguy, N. et al. 2013. New handbook for standardise measurement of plant functional traits worldwide. Australian Journal of Botany 61: 167-234.

34.

Puc-Kauil, R., Ángeles-Pérez, G., Valdéz-Lazalde, J.R., Reyes-Hernández, V.J., Dupuy-Rada, J.M., Schneider, L., Pérez-Rodríguez, P. and García-Cuevas, X. 2020. Allometric equations to estimate above-ground biomass of small-diameter mixed tree species in secondary tropical forests. iForest-Biogeosciences and Forestry 13(3): 165.

35.

QGIS.org. 2024. QGIS Geographic Information System. Open Source Geospatial Foundation Project. Version 3.36.3-Maidenhead. Retrieved from https://qgis.org.

36.

Qin, G., Li, R., Zou, W., Yu, N., Yang, J., Yin, G., Wang, Z. and Chen, Z. 2020. Estimating biomass partitioning in Mytilaria laosensis using additive models. Austrian Journal of Forest Science 137(2): 85.

37.

Rue-Johns, A.Z., Crotteau, J.S., D’Amore, D.V. and Barnard, J.C. 2021. Biomass regressions for understory species in young-growth Sitka spruce–western hemlock forests of southeast Alaska. Northwest Science 95(1): 114-124.

38.

Saglam, S., Ozdemir, E., Ozkan, U.Y., Demirel, T. and Makineci, E. 2020. Biomass estimation of aboveground tree components for Turkey oak (Quercus cerris L.) in south-eastern Turkey. Environmental Monitoring and Assessment 192: 1-12.

39.

Son, Y.M., Kim, R.H., Lee, K.H., Pyo, J.K., Kim, S.W., Hwang, J.S., Lee, S.J. and Park, H. 2014. Carbon emission factors and biomass allometric equations by species in Korea. Korea Forest Research Institute. Seoul, Republic of Korea. pp. 97.

40.

Sprugel, D.G. 1983. Correcting for bias in log-transformed allometric equations. Ecology 64(1): 209-210.

41.

Van Den Bor, B., Castro-Díez, P. and Alonso, Á. 2024. Above and belowground carbon stock of pine plantations and native oak forests coexisting in central Spain. New Forests 55(4): 941-959.

42.

Yadav, S. and Sanyam S. 2016. Analysis of k-fold cross-validation over hold-out validation on colossal datasets for quality classification. 2016 IEEE 6th International conference on advanced computing (IACC). IEEE. Bhimavaram, India. pp. 78-83.

43.

Yuen, J.Q., Fung, T. and Ziegler, A.D. 2016. Review of allometric equations for major land covers in SE Asia: Uncertainty and implications for above-and below-ground carbon estimates. Forest Ecology and Management 360: 323-340.

44.

Zeng, W.S. 2014. Development of monitoring and assessment of forest biomass and carbon storage in China. Forest Ecosystems 1: 1-10.

45.

Zianis, D. and Mencuccini, M. 2004. On simplifying allometric analyses of forest biomass. Forest Ecology and Management 187(2): 311-332.