서 론
산사태는 돌발적으로 산지 사면이 붕괴하여 비탈면을 따라 이동하는 현상으로, 직접적인 인명 및 재산 피해를 초래할 수 있는 대표적인 자연재해 중 하나이다. 특히, 최근 우리나라의 산사태 피해 규모는 극한 호우로 인해 대형화되는 추세로, 산사태 피해를 선제적으로 예방하고 관리하기 위해서는 잠재적 산사태 발생확률인 산사태 위험도(Landslide hazard)를 정량적 또는 정성적으로 평가하는 것이 중요하다(Varnes, 1984; Fell et al., 2008; Yang et al., 2023; Kim, 2024).
이러한 선제적 재난 대응에 대한 산사태 위험도 평가의 중요성으로 인해 국내·외에 걸쳐 많은 선행연구가 수행되고 있다. 국내의 경우, 통계적 기법과 물리적 기법을 활용한 산사태 위험도 평가가 주를 이루는 것으로 확인되며, 특히 산림청에서 통계적 기법을 활용하여 10 m×10 m 격자 단위의 전국 산사태 위험지도를 구축하고 산사태 위험도를 5등급으로 구분하여 선제적 재난 대응 활동을 수행하고 있다(NIFoS, 2023). 또한, 최근에는 기계학습, 심층학습 및 인공지능 등을 통한 데이터 기반(Data driven)의 분석과 기후변화와 지진 등의 산사태 피해 발생 유인변화에 대응하기 위한 연구가 많이 수행되었다(Al et al., 2019; Seo et al., 2021; Ahn et al., 2023; Cha et al., 2023). 국외의 경우도 통계적·물리적 기법에서부터 데이터 기반 분석 등, 다수의 연구가 수행되고 있다(Baum et al., 2008; Huang et al., 2022b; Zeng et al., 2023; Hong, 2024).
산사태 위험도 평가를 위해서는 분석 규모의 단위 설정이 필수적으로, 산사태 위험도 평가에 사용되는 분석 단위는 (i)격자 단위(Grid unit), (ii)지형 단위(Terrain unit), (iii)고유 요소 단위(Unique condition unit) 단위, (iv)사면 단위(Slope unit), (v)지형-수문학적 단위(Geo-hydrological unit), (vi)지형학적 단위(Topographic unit) 및 (vii)정치·행정적 단위(Political·Administrative unit)가 사용된다(Reichenbach et al., 2018). 다만, 분석 용이성의 확보와 최소 단위 분석을 위해 보편적으로 격자 단위의 분석이 이용된다(Zhao and Zhoa, 2020; Huang et al., 2022a). 그러나, 격자 단위 분석은 개별 격자를 독립적인 단위로 사용함으로 각 격자의 개별 특성만을 나타내기 때문에 지형의 구조적 특성을 반영하기 어렵고 정책·행정적 측면에서 산사태 위험도 관리 및 대응의 실용성이 낮다(Tian et al., 2010). 반면, 사면 단위는 계곡선과 능선을 기준으로 구분되는 영역을 분석 단위로 사용함으로 지형의 구조적 특성을 반영할 수 있으며 위험도의 실질적 관리와 같은 목적에 따라 격자 단위와 함께 산사태 위험도 평가의 주요 분석 단위로 활용된다(Tsai et al., 2018; Tanyas et al., 2018; Liu et al.. 2022; Jiazhu et al., 2023; Sun et al., 2023).
사면 단위를 이용한 위험도 분석 사례의 경우, Alvioli et al.(2020)은 경사 방향의 지형 균질성을 최대화하는 사면 단위 분할 최적화 알고리즘을 개발하고 이탈리아 전역에 적용 후 군집 분석하여 사면 단위를 산사태 위험도 평가에 활용할 수 있음을 입증하였다. Ma et al.(2023)은 지진 유발 산사태에 대해 분석 단위를 기반으로 산사태 위험도를 분석하여 사면 단위를 기반한 위험도 모형의 불확실성이 격자 단위에 비해 낮음을 밝힌 바 있다. Moreno et al.(2024)은 강우 유발 천층붕괴의 위험도를 예측하고 강우 조건의 동적 변화에 따른 임계치 산출을 위한 사면 단위의 공간·시간적 데이터 기반 모형화를 수행하였으며 모형의 AUROC(Area Under the Receiver Operating Characteristic Curve)는 약 0.85 이상으로 나타났다. 선행연구 사례를 빗대어 사면 단위를 이용한 산사태 위험도 평가의 적용성을 확인할 수 있으나 국내의 연구사례는 아직 미흡한 실정이다.
따라서, 본 연구에서는 산림청의 산사태 위험지도 평가기법을 기반으로 격자 단위와 사면 단위의 비교를 수행하여 사면 단위의 산사태 위험도 및 위험등급 평가 활용 가능성을 검토하고자 하였다.
다만, 국내에서는 산사태 위험도와 산사태 취약성에 대한 개념이 혼용되는 실정이다. Azemeraw(2021)과 Park and Lee(2022)에 따르면, 산사태 위험도는 특정 공간·시간적 범위에서 산사태가 발생할 잠재적인 확률(Probability)로 정의하며 산사태 취약성(Landslide Susceptibility)은 특정 공간 범위에서 산사태가 발생할 수 있는 공간적 가능성(Likelihood)으로 두 개념을 분리하고 있다.
이를 산림청의 산사태 위험지도에 대입할 경우, 산출 결과는 산사태 취약성에 유사하나 산사태 위험도로써 이를 설명하고 있다. 이에 따라, 이 연구에서는 개념의 혼용이 존재하지만 기존 산사태 위험지도의 제작 방법을 활용함으로 용어의 통일성을 위해 모형의 산출 결과를 산사태 위험도와 위험등급이라 표현한다.
재료 및 방법
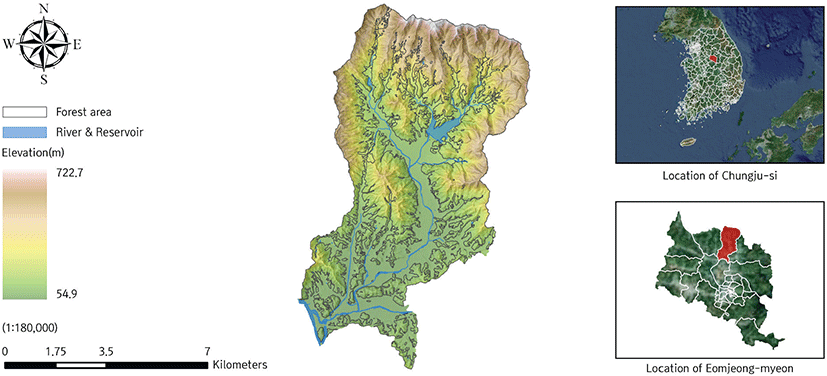
본 연구는 충청북도 충주시 엄정면 일원으로, 대상지는 2020년 7~8월 집중호우에 따른 산사태 피해가 집중적으로 발생하였으며, 이로 인한 인명피해와 재산 피해 이력이 존재하고 지속적인 산사태 피해 발생이 확인된다. 대상지의 공간적 범위는 북위 37°3’~37°10’와 동경 128°52’~128°58’사이로 충주시의 서·남부에 위치하며 해발고도는 약 55~723 m이고, 면적은 약 56.2 km2이다(Figure 1).
대상지는 흑운모 화강암으로 지배되는 특성을 보유하며, 일부 지역에서는 편상 화강암의 특징이 확인되고 다양한 방향성을 가진 절리와 슐리렌이 발달하고 일부 절리는 변이된 상태이다(KIGAM, 1971).
절리의 발달은 풍화를 촉진함을 미루어 볼 때, 화강암의 풍화 과정에서 밀도가 감소할 수 있으며 이는, 절리와 슐리렌 구조가 분포하는 대상지의 암반 내 공극이 확대되며 구조적 강도가 낮아지며 풍화가 가속될 가능성이 있음을 시사한다(Jung et al., 2009). 특히, Kim et al.(1998)은 화강암에서 산사태 발생 취약성이 다른 암질에 비하여 높음을 밝힌 바 있다. 충주지역의 최근 10년(’15~’24) 평균 강수량은 약 1,225 mm로, 6~9월 여름철에 전체 강우의 약 68%가 집중되는 등의 산사태 발생 위험성이 여전히 존재한다. 특히, 2024년 11월 기준, 인구통계를 따르면 엄정면의 총인구는 2,992명이며, 주민의 대부분이 농림업에 종사함으로 산사태 피해에 대한 사회적 취약성이 높다.
본 연구는 Figure 2와 같이 (1)분석 단위 추출 및 중첩분석 단계, (2)분석 단위별 산사태 위험도 및 위험등급 평가 단계, (3)분석 단위별 산사태 위험도 및 위험등급 검토 단계와 같이 총 3단계로 구분하여 수행되었으며, 분석 간 활용한 자료는 Table 1과 같다.
| Data | Source | Scale |
|---|---|---|
| Forest type map | KFS | 1:25000 |
| Forest soil map | KFS | 1:25000 |
| Digital topographic map | NGII | 1:5000 |
| Digital geologic map | KIGAM | 1:50000 |
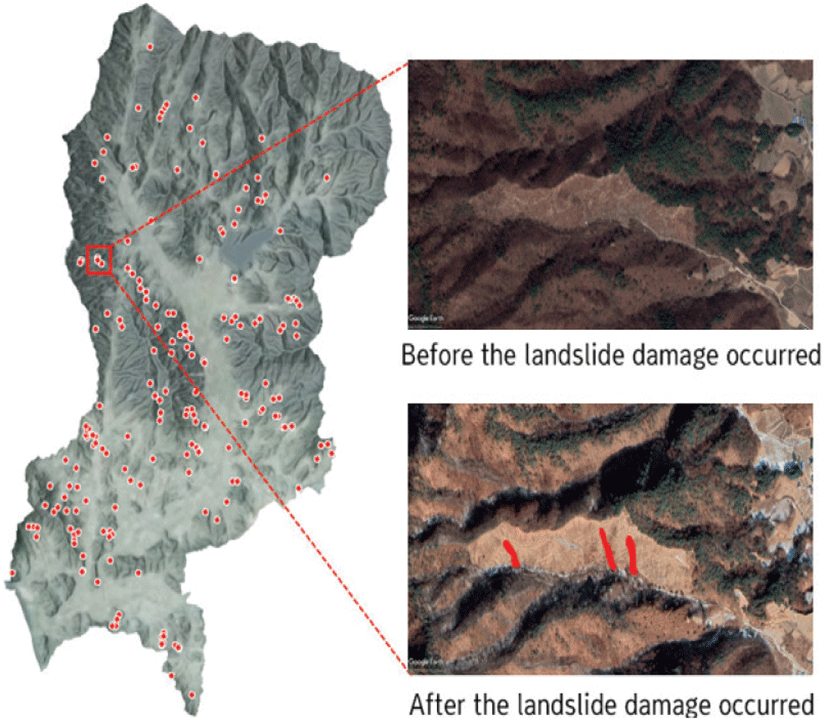
분석 단위 추출 및 중첩분석 단계는 검증 자료로 사용될 산사태 피해지 자료의 구축과 공간정보의 명확성을 확보하기 위해 수행한다. 먼저, 산사태 위험성 평가 검증을 위한 산사태 인벤토리는 행정안전부의 생활안전지도에서 제공하는 산사태 발생 이력 정보(’16~’23)를 활용하였다. 다만, 산사태 발생 이력 정보 내에는 발생일시, 발생원인, 피해지 주소만이 존재함으로 웹사이트를 통해 확인되는 엄정면의 자료를 별도로 확인하였으며, 확인된 192개소의 발생 이력을 토대로 Google Earth Pro(Ver 7.3.6., Google, California, U.S.A.)의 Time Slider 기능을 활용하여 시계열 분석을 수행하였으며 피해 원형이 확인되는 131개소의 피해지를 직접 구축하였다(Figure 3).
구축한 각 산사태 피해지 공간정보는 피해 범위 내 최대 표고로 확인되는 지점을 발생원으로 가정하여 격자 단위와 사면 단위 분석 결과에 대한 검증 자료로 이용하였다. 산사태 발생원의 추출은 ArcGIS Pro(Ver 3.4.2., ESRI, California, U.S.A.)를 이용하여 산사태 피해지 공간정보와 공간해상도 10 m급의 수치표고모형을 중첩 분석하여 산사태 피해지별 최대 표고점을 추출하였다(Figure 4).
격자 단위는 산사태 위험지도 산정기법을 통해 획득하였으며, 사면 단위의 추출은 GRASS GIS(Ver 8.3.1., GRASS development Team, Open Source Geospatial Foundation, U.S.A.)환경 하에 Alvioli et al.(2016)이 개발한 r.slopeunits 모듈을 이용하였다. 구동에 필요한 매개변수 설정은 표준화된 값의 제공이 되지 않아, 계수를 조정하며 0.25 m 항공정사영상을 토대로 실제 지형과의 일치성이 가장 높은 경험적 계수를 적용하였다(Table 2). t는 흐름 축적의 초기 임계치(m2), a는 사면의 최소면적(m2), c는 경사 방향으로의 원형 분산 정도, r은 t에 대한 반복 감소 계수, m은 최대 반복 횟수이다.
| Parameter | Value | Unit |
|---|---|---|
| t | 5000 | m2 |
| a | 5000 | m2 |
| c | 0.05 | - |
| r | 1 | - |
| m | 10 | - |
이후, Table 1의 열거된 자료를 중첩 분석하여, 분석 단위별 산림환경특성을 검토하였다.
다만, r.slopeunits는 수문학적 분류를 통한 사면 단위 추출을 기반함으로 공간해상도가 적절하지 않거나 수계학적 연결 관계의 탐색이 어려운 경우 등에 의해 단일 셀이 분석 범위로 인식되거나 국소 사면으로 분할되는 등의 기하학적 문제가 발생한다. 이에 따라, 본 연구에서는 식 1에서 식 3을 통해 기하학적 문제를 자동 검출하고 보정 처리하였다(Figure 5).
식에서, SU는 전체 사면의 집합, s는 특정사면, At는 면적 최솟값(m2), SUsmall은 At 이하 사면의 부분집합, 는 특정사면 i의 경계, L은 와 간의 길이, N(si)는 특정사면 si와 경계를 공유하는 이웃 사면의 집합, Aq는 이웃 사면 중 면적이 가장 큰 사면, smerged는 처리 사면이다.
해당 식에서 설정할 수 있는 값은 At이며, 이 연구에서는 10 m급 공간해상도에서 산출될 수 있는 가장 작은 기하학적 오류 면적인 1,000 m2를 면적 최솟값으로 설정하였다.
분석 단위별 산사태 위험도 평가는 산사태 위험지도의 위험도 산정 방안과 같고, 이는 식 4와 식 5를 통해 산정된다(Woo et al., 2014; NIFoS, 2023). 산사태 위험등급은 식 5로부터 산출되는 H에 대해 Table 3의 기준을 적용하여 구분한다.
| Grade | Range |
|---|---|
| 1 | LS ≥ 0.121 |
| 2 | 0.121 > LS ≥ −0.425 |
| 3 | −0.425 > LS ≥ −1.097 |
| 4 | −1.097 > LS ≥ −2.441 |
| 5 | −2.441 > LS |
식에서, LS는 산사태 발생확률, S는 사면 경사(°), L은 사면 길이(m), C는 사면 곡률, D는 경급, SD는 토심(cm), A는 사면 방위, B는 모암, F는 임상, H는 산사태 위험도, a는 상부사면 기여면적, β는 경사(Radian)이다. 범주형 자료에 대한 인자값 설정은 NIFoS(2023)를 참고하여 적용하였다.
다만, 사면 단위의 산사태 위험도 평가는 기하학적 문제가 처리된 사면에 대해 중첩분석을 수행하되 연속형 자료는 사면 내 자료의 평균값을 이용하고, 범주형 자료는 사면 내 자료의 최빈값을 이용하여 산사태 위험도와 위험등급을 산정하고, 기술통계 분석을 수행하였다.
분석 단위별 위험도 및 위험등급 검토는 격자 단위와 사면 단위로 산출된 위험도와 위험등급을 검증 자료와 대조하고 각 분석 단위별 평가 결과를 비교 및 통계 분석하기 위해 R(Ver 4.2.2., R Foundation, Vienna, Austria)을 이용해 연속형 자료(위험도)와 범주형 자료(위험등급)를 구분하여 통계 분석하였다.
위험도의 비교는 분석 단위별 일치도를 평가하기 위해 윌콕슨 부호 순위 검정(Wilcoxon signed-rank test)을 수행하였으며, 검정 결과에 대한 실질적 크기의 산정을 위해 Cohen’s d를 이용하여 효과 크기를 분석하였다.
위험등급의 비교는 두 범주형 자료의 등급 분포양상과 차이를 확인하기 위해 카이제곱 검정(Chi-Square Test)을 이용하여 동질성(Homogeneity)과 독립성(Independence)을 분석하였다(Wilcoxon, 1945; Cohen, 1988).
결과 및 고찰
발생원을 기반한 격자 단위의 중첩분석 결과는 Figure 6과 Table 4와 같다.

C: Coniferous forest, Y: Young growth reproduction
발생원과 중첩된 격자 단위의 평균 경사는 약 23.9±7.4°로, 급경사지(20~25°)에서 다수 분포한다. 평균 사면 길이는 약 51.6±53.8 m로 변동성이 크게 나타나며 이는 사면 하부 또는 소규모 산사태가 포함되어 나타나는 결과로 판단된다. 평균 곡률은 약 −0.89±2.78로 Suzuki(1977)에 의한 분류 결과, 오목한 지형에서 다수 분포하나 자료의 변동성이 크게 나타난다. 평균 TWI는 약 3.1±1.3으로 전체 대상지의 평균 TWI 값인 약 2.9±1.4보다 소폭 높은 경향이 확인되어 상대적으로 습윤한 지형으로 나타났다. 평균 토심은 약 52±22.3 cm로 얕은 토심에서 발생한 것으로 나타나나 이는 입력자료의 한계로 전토심이 아닌 유효토심 자료를 사용한 결과로 판단된다. 임상은 침엽수림이 최빈값으로 확인되며, 경급은 치수, 모암은 흑운모 화강암, 방위는 남동이 최빈값으로 나타났다.
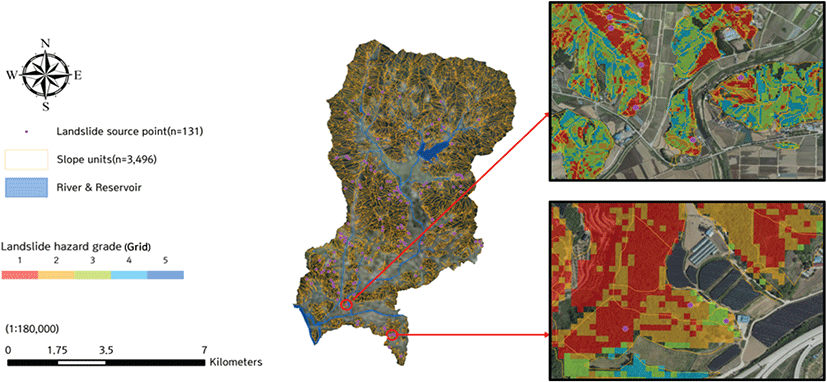
사면 단위 추출 결과, 대상지는 총 3,496개의 산지 사면으로 구분된다(Figure 7). 추출된 산지 사면 내 산사태 피해 발생 사면의 중첩분석 결과는 Table 5와 같다.
B: Broadleaf forest, M:Medium diameter wood
평균 면적은 약 10,302±9,856 m2이며, 5,000 m2 이하의 사면이 2,263개로 약 65% 수준인 것으로 나타났다. 사면의 평균 경사는 약 22.6±6.3°로 격자 단위 중첩분석 결과에 비해 다소 낮게 나타났다. 이는 분석 단위의 확대로 인해 산지 하부, 경사가 감소하는 구간이 포함된 결과로 판단된다. 평균 사면 길이는 약 60.5±98.8 m로 격자 단위 중첩분석 결과에 비해 높게 나타나나 변동성 또한 상승하는 것으로 확인된다. 소규모 사면이 포함되어 나타나는 결과로 판단된다.
평균 사면 곡률은 약 0.16±1.13으로 볼록한 유형의 사면이 다수 추출되었다. 볼록한 사면의 추출이 다수 확인되는 것은 사면 단위 추출 기법에 기인하는 것으로, 사면 단위는 계곡선과 능선을 기준으로 사면을 분류함으로, 계곡선이 경계면으로 작용하는 사유로 판단된다.
사면 평균 TWI는 약 3.0±2.9로 격자 단위 중첩분석 결과에 비해 소폭 낮게 나타나나 변동성은 크게 나타난다. 이는 경사의 경우와 같이 분석 범위의 확대에 따른 결과로 판단된다. 사면 내 평균 토심은 약 48.7±16.6 cm로 격자 단위 추출에 의한 발생원 중첩분석 결과에 비해 낮게 나타났다. 임상은 활엽수림이 최빈값으로 나타났으며, 경급은 중경목, 모암은 흑운모 화강암, 사면 방위는 북서로 확인된다.
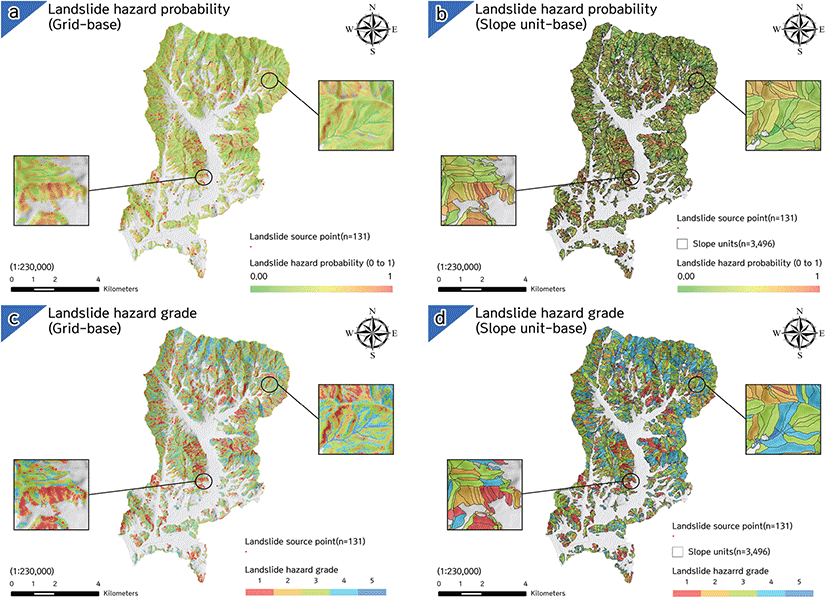
분석 단위별 산사태 위험도 및 위험등급 분석 결과는 Figure 8과 같고, 산사태 발생원에 대한 분석 단위별 산사태 위험도와 위험등급의 기술통계 결과는 각각 Table 6 및 Table 7과 같다.
| Class | Value | ||||
|---|---|---|---|---|---|
| max | min | avg | std | ||
| Landslide hazard probability | Grid | 0.79 | 0.05 | 0.42 | 0.17 |
| Slope unit | 0.72 | 0.02 | 0.40 | 0.16 | |
| Class | Count | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Landslide hazard grade | Grid | 28 | 32 | 41 | 25 | 5 |
| Slope unit | 36 | 31 | 42 | 21 | 1 | |
평가 결과에서 산사태 위험도의 경우, 격자 단위가 사면 단위에 비해, 모든 항목에서 소폭 높게 나타났으나 위험등급은 사면 단위가 위험 구간(1·2등급)에서 우세한 경향을 보였다. 이는 중첩분석 결과와 같이 분석 범위의 확대에 기반한 결과로 판단된다. 사면 단위는 격자 단위와 달리 평균화가 수행되어 위험도의 변동성이 감소하게 된다. 반면, 격자 단위는 국지적(특정 격자) 특성만을 반영함으로 극단적인 값이 산출될 가능성이 있어 변동성이 상대적으로 크게 나타나는 것으로 판단된다. 즉, 사면 단위는 국지적 특성에 기반하는 격자 단위와 달리 구조적 특성을 기반하여 공간적 분할이 이뤄짐으로 변동성이 격자 단위에 비해 상대적으로 낮으며 극값의 출현 빈도 또한 낮다. 다만, 평균화에 따른 위험도 산출 결과는 절대적으로 과소 평가되는 것이 아니며 과대 평가될 가능성 또한 존재한다.
이에 따라, 사면 단위는 MAUP(Modifiable Areal Unit Problem)와 관련한 문제점을 내포함으로 사면 단위 기반의 산사태 위험도를 분석할 시, 적정 공간해상도와 분할 면적 기준 수립과 관련한 추가적인 연구가 필요할 것으로 판단된다.
요약하여, 사면 단위 기반의 분석은 지형의 구조적 특성을 반영할 수 있으나, 격자 단위와 달리 국지적인 위험 구간의 추출이 불가한 한계점이 존재한다.
이와 달리, 격자 단위 기반의 분석은 국지적인 위험 구간의 추출은 가능하나, 분석 결과는 각 격자의 개별 특성으로써 관리적 측면에서의 활용성이 사면 단위에 비해 상대적으로 낮다.
특히, Kim et al.(2022)에 따르면, 격자 단위의 산사태 위험도 분석은 종합적인 재해 영향을 반영하기 어려움으로, 실질적 재해 대응을 위해서는 공간적 분석 범위의 확대가 필요하다고 시사한 바를 미루어, 사면 단위의 적용을 고려할 수 있다.
본 연구에서는 사면 단위 사용에 있어 평균화에 따라 값의 저하가 확인되었으나 실제 산사태 피해 지점에 대한 분석 단위별 결과는 크게 다르지 않았다.
따라서, 포괄적 재난 대응 및 관리적 측면에서 사면 단위의 산사태 위험도 및 위험등급 분석은 장점을 보유하는 것으로 판단된다.
분석 단위별 산사태 위험도 결과에 대한 Shapiro-Wilk 정규성 검정 결과, 사면 단위의 위험도 결과에서 p<0.05의 수준으로 정규성 가정을 만족하지 않는 것으로 나타났다(Table 8).
| Class | Shapiro-Wilk test result | |
|---|---|---|
| W-statistic | p-value | |
| Grid | 0.98 | 0.38 |
| Slope Unit | 0.95 | 1.8E-04 |
이에 따른, 윌콕슨 부호 순위 검정 결과, p<0.05의 수준으로 분석 단위별 위험도 분석 결과 간의 유의성이 존재하며, 이는 Zhuang et al.(2016)과 Huang et al.(2024)이 시사한 바와 같이, 격자 단위와 사면 단위의 분석 방법의 차이에 기인한 것으로 판단된다[Figure 9(a)].

다만, Eboh et al.(2021)이 시사한 바와 같이, 윌콕슨 부호 순위 검정 결과의 유의성이 존재하는 것은 윌콕슨 부호 순위 검정이 데이터의 분포를 고려하지 않고 중앙값을 고려하기 때문으로, 비모수적 효과 크기 지표를 고려하여 결과의 실질적인 차이를 분석해야 한다.
이에 따라, Cohen’s d를 이용한 효과 크기 분석 결과, d(효과 크기)는 0.161의 수준으로 격자 단위와 사면 단위의 산사태 위험도 평가 결과는 방법론적 차이에 의한 통계적 유의성은 존재하나 실질적인 차이가 존재하지 않는 것으로 나타났다[Figure 9(b)]. 즉, 격자 단위와 사면 단위 간 산사태 위험도 평가의 통계적 차이에도 불구하고 실질적인 차이가 없으므로, 예측 모형의 정확도와 현장 적용에 큰 영향이 없는 것으로 판단된다.
카이제곱 검정을 이용한 분석 단위별 산사태 위험등급 검토 결과, 동질성의 유의 확률은 p>0.05의 수준이며 χ2 = 4.04로, 통계적 유의성이 나타나지 않았다[Figure 10(a)]. 즉, 두 분석 단위에서 산출된 위험등급 분포에는 통계적으로 유의한 차이가 존재하지 않아 두 분석 단위별 위험등급 평가 체계의 일관성이 존재한다고 볼 수 있다.
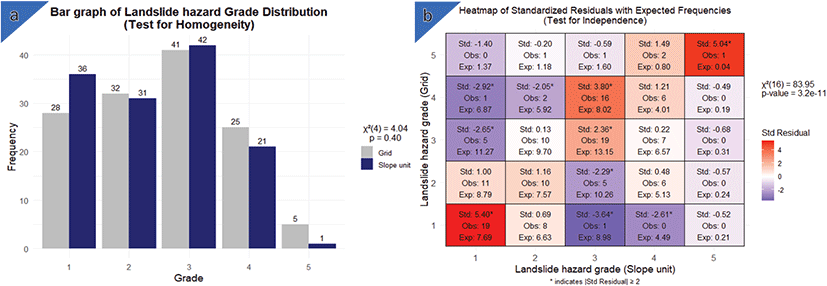
위험등급 분포가 유사한 경향으로 나타난 것은, 분석 단위별 중첩분석 결과와 같이 지형적 동질성에 기인한 것으로 판단되며, 효과 크기 분석 결과에 근거하여 실질적인 차이가 부재한 결과로 판단된다.
독립성 검정 결과, 유의 확률은 p<0.05의 수준이며 χ2 은 83.95로, 분석 단위별 위험등급의 분포는 통계적 유의성이 존재하는 것으로 나타났다. Heatmap plot으로 결과를 확인할 경우, 특히 두 분석 단위에서 1등급과 5등급으로 분류되는 조합의 표준화 잔차(Standardized residual)가 각각 약 5.40과 5.04로 확인되어, 동일 산사태 피해지에 대해 두 분석 단위 모두 고위험(1등급)과 저위험(5등급)으로 분류되는 빈도가 기대치보다 크게 나타났다[Figure 10(b)].
다만, 중간 위험등급(2~4등급)의 경우는 음의 표준화 잔차가 확인되어 관측 빈도가 기대치보다 낮은 경향을 보였다. 이는 두 분석 단위가 고위험과 저위험과 같은 극단적 평가에 대해서는 일관된 분류 경향을 보이나 중간 위험등급에 대한 평가 분류 결과는 상대적으로 불일치가 존재함을 의미한다.
이러한 두 분석 단위 간의 비독립성은 산사태 위험등급 산정에 선행되는 산사태 위험도 평가 과정의 차이와 평균화로부터 기인하는 것으로 판단되어 분석 목적에 따른 분석 단위의 설정이 필요할 것으로 판단된다.
특히, Woodard et al.(2023)의 선행 연구를 참고할 경우, 공간해상도에 따라 공간적인 추세와 통계적 특성이 상이해질 가능성이 존재한다. 이는, 격자 단위 분석 방법인 산사태 위험지도 제작 방법을 사면 단위에 적용할 경우, 공간적 세분성의 저하와 사면 단위별 불균질성으로 정밀도가 저하될 가능성이 존재하고, 입력 인자의 평균화 또는 단순화(최빈값 이용)에 대한 추가적 정밀도 문제가 존재함으로 한계점이 존재하여, 추후 사면 단위를 기준으로 한 산사태 위험도 평가 모형 개발 연구가 필요할 것으로 판단된다.
또한, 사면 단위 분석의 경우, 분석 단위의 면적이 상이함으로 이에 따른 통계적 왜곡이 발생할 가능성이 존재한다. 다만, 관련 연구사례가 미비한 실정으로 이 연구에서는 적용하지 못한 한계점이 존재한다. 향후 면적-가중 평균(Area-|Weighted Mean) 또는 면적 기반의 보정 통계량을 산출 및 적용하여 사면 단위의 상이한 면적 차이를 고려한 연구가 필요할 것으로 판단된다.
다만, Chen and Wu(2016)은 위험도 평가 및 재난 관리 정책 수립 측면에서, 로지스틱 회귀 분석 모형과 같은 통계적 모형에 사면 단위 기반 산사태 위험도 분석을 적용할 시 효율성과 실용성을 보유함을 시사한 바 있으며, Woodard et al.(2024)은 사면 단위를 통한 산사태 위험 구역 산출 시, 사면 단위가 격자 단위에 비해 직관적이고 명확한 산사태 위험 구역의 구분을 가능하게 하여, 산사태 피해의 사전 예방과 조기 대응 차원에서의 보수적 접근이 가능함을 밝힌 바 있다.
특히, 산림청은 산사태 발생 우려지역에 대한 기초 및 실태조사를 수행하고 있으며, 피해 유형(산사태·토석류)에 따라 평가를 달리한다.
다만, 기초조사 중 토석류 유형이 유역을 기초 공간 단위로 하는 것에 반해 산사태 유형은 공간 단위 설정이 미비한 실정이다.
이에 따라, 토석류 유형에서 산사태 위험지도를 통해 평가하는 황폐 발생원에 대한 검토가 사면 단위에서는 배제되는 실정이고, 사면을 대상으로 조사하는 산사태 유형은 사면의 설정부터 평가까지 작업자의 경험과 지식에 좌우된다.
따라서, 공간적 기초 단위의 설정을 통해 조사와 평가 방법을 일원화할 필요성이 존재한다. 또한, 사면 단위를 도입할 경우, 공간 단위별 통합 산림 관리체계의 마련이 가능할 것으로 판단된다. 이는 기존에 목적별로 상이하게 분리되어 관리되는 공간적 단위를 (1단계)유역 단위→(2단계)사면 단위→(3단계)격자 단위로 연결하여 공간적 기준을 세분화하고 기초 공간 단위를 유역으로 설정하여 사면 단위와 격자 단위를 유역의 하부 요소로 관리하는 등의 체계적이며 효율적인 산림 관리방안을 수립할 수 있을 것으로 기대된다.
종합하여, 산사태 위험도 및 위험등급 평가에서 사면 단위 기반의 분석을 수행할 경우, 정책·행정적 관리 측면에서의 효율성과 실용성을 보유하나 격자 단위와 달리 일관된 분석 체계의 유지 및 국지적 세부 특성 산출의 한계점을 나타낸다. 따라서, 재해 관리적 측면 또는 심층적 분석과 같은 재해 평가적 측면 등을 고려하여 활용 목적에 따른 분석 단위의 설정이 필요하며 분석 단위의 변경에 따른 통계적 차이와 분류 특성 등을 고려해야 할 것으로 판단된다.
결 론
본 연구에서는 산사태 위험도와 산사태 위험등급 평가에 있어 사면 단위의 활용 가능성을 검토하고자 사면 단위와 격자 단위의 평가 결과 비교를 수행하였으며, 본 연구를 통해 얻은 결론은 다음과 같다.
(1) 사면 단위 기반의 산사태 위험도 및 위험등급 평가는 기존 격자 단위 분석과 비교할 경우, 포괄적인 재난 대응 및 관리 측면에서 유용할 것으로 판단된다. 다만, 사면 단위 분석은 공간적 범위 확대와 구획화 및 평균화 등에 따라 격자 단위와 같이 국지적 위험 구간의 산출이 불가한 한계를 내포한다.
(2) 위험도 평가 결과에 대해 실시한 윌콕슨 부호 순위 검정 결과, 방법론적 차이로 인해 두 분석 단위의 산사태 위험도 평가 결과에 통계적으로 유의미한 차이가 존재하였으나, 효과 크기 분석에서는 실질적인 차이가 미미한 것으로 나타났다. 이는 평가 대상의 세부 특성 차이가 통계적 검정에서는 존재하여도, 재난 관리와 같은 실제 적용 단계에서의 차이는 상대적으로 낮음을 시사한다.
(3) 위험등급 평가 결과에 대해 실시한 동질성 검정 결과, 격자 단위와 사면 단위의 위험등급 분포는 통계적 유의성(p>0.05, χ2=4.04)이 없는 것으로 확인되나, 독립성 검정 결과에서는 통계적 유의성(p<0.05,χ2=83.94)이 존재하는 것으로 나타났다. 특히, 분석 단위가 상이하더라도 고위험과 저위험 등급으로 분류되는 빈도는 기대치보다 높게 나타났으나 중간 위험등급에서의 상대적 불일치가 존재함으로 분석 단위별 평가 방법을 체계화하고, 실용성과 적용성 등을 검토할 필요성이 존재한다.
(4) 종합하여, 사면 단위 기반 분석은 격자 단위 기반 분석과 달리 국지적 위험 구간의 산출은 불가하나, 전반적인 재난 대응 및 예방 측면에서 효율성을 보유하는 것으로 판단된다. 따라서, 산사태 위험 평가 및 재난 대응 전략 수립 시 목적에 따라 분석 단위를 설정하여 활용한다면 산사태 위험 평가의 신뢰성과 실용성을 강화할 수 있을 것으로 판단된다.