Article
최근 12년간 아까시나무 만개일의 변화와 과정기반모형을 활용한 지역별 만개일 예측
김수경1,
김태경1,
윤석희2,
장근창3,
임혜민4,
이위영4,
원명수3,
임종환5,
김현석1,6,7,8,*

Recent Changes in Bloom Dates of Robinia pseudoacacia and Bloom Date Predictions Using a Process-Based Model in South Korea
Sukyung Kim1,
Tae Kyung Kim1,
Sukhee Yoon2,
Keunchang Jang3,
Hyemin Lim4,
Jong-Hwan Lim4,
Wi Young Lee3,
Myoungsoo Won5,
Hyun Seok Kim1,6,7,8,*

Author Information & Copyright ▼
1Department of Agriculture, Forestry and Bioresources, Seoul National University, Seoul 08826, Korea
2Korea Association of Soil and Water Conservation, Cheongju 28165, Korea
3Forest ICT Research Center, National Institute of Forest Science, Seoul 02455, Korea
4Forest Tree Improvement and Biotechnology Division, National Institute of Forest Science, Suwon 16631, Korea
5Forest Ecology Division, National Institute of Forest Science, Seoul 02455, Korea
6Interdisciplinary Program in Agricultural and Forest Meteorology, Seoul National University, Seoul 08826, Korea
7National Center for Agrometeorology, Seoul National University, Seoul 08826, Korea
8Research Institute for Agricultural and Life Sciences, Seoul National University, Seoul 08826, Korea
ⓒ Copyright 2021 Korean Society of Forest Science. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received: May 13, 2021; Revised: Jun 29, 2021; Accepted: Jun 29, 2021
Published Online: Sep 30, 2021
요 약
최근 급격한 봄철 기온 상승과 기후변화의 영향으로 한반도에 분포하고 있는 아까시나무의 개화 시기가 변화하면서 지역간에 동시 개화 현상(simultaneous blooming)이 관측되고 있다. 이러한 변화는 국내 양봉 산업에 큰 변화를 초래하였고, 이로 인해 정확도 높은 아까시나무 개화시기 정보에 대한 수요가 증가하고 있다. 따라서, 본 연구를 통해 아까시나무의 지역별 개화 시기 변화를 잘 설명할 수 있는 신뢰도 높은 개화 시기 예측 모형을 개발하고자 하였다. 이를 위해 지난 12년(2006~2017년)간 전국 26개 지점에서 관측된 아까시나무 만개일 자료와 과거 일기온 복원 자료를 활용하여 봄철 기온 및 아까시나무 만개일 변화의 경향성을 권역별로 파악하고, 과정기반모형을 활용하여 지역 통합 모형(SM)과 함께 지역적 특성을 반영하는 세 모형-SM에 지점별 보정계수를 도입한 수정 통합 모형(MSM), 권역별로 모수를 추정하는 권역별 통합 모형(GM), 관측 지점별로 모수를 추정하는 지역 모형(LM)-을 도출, 성능을 비교하였다. 기온 및 만개일의 경향 분석 결과, 남부 지역에 비해 봄철 기온 상승률이 2배 이상 높았던 중북부 내륙 지역의 경우 만개일이 빠른 속도로 앞당겨져, 결과적으로 남서부 해안 지역과의 만개일 차이는 1년에 0.7098일씩 감소하였다(p-value=0.0417). 전체 지역에 대한 모형의 성능 비교 결과, 지역 특이성이 반영되지 않은 SM에 비해서 MSM은 24% 이상, LM은 15% 이상 감소한 RMSE 값을 나타냈다. 또한 LM과 MSM의 예측 알고리즘을 전국 범위로 확대하여 4년 간(2014~2017년) 16개의 추가 관측 지점을 대상으로 검증한 결과, LM에 코크리깅(Co-kriging)기법을 적용한 방법이 보정계수 전국 분포도를 추정하여 SM을 보정하는 방법보다 예측력이 더 뛰어났으며, 오차의 분포는 두 모형 간에 통계적으로 유의한 차이를 보였다(RMSE: p-value=0.0118, Bias: p-value= 0.0471). 본 연구는 아까시나무의 개화 시기 예측에 있어 지역 단위 예측의 신뢰도를 향상시키고 모형을 넓은 지역 범위로 확대, 적용하기 위한 방안을 제시하였다.
Abstract
Due to climate change and its consequential spring temperature rise, flowering time of Robinia pseudoacacia has advanced and a simultaneous blooming phenomenon occurred in different regions in South Korea. These changes in flowering time became a major crisis in the domestic beekeeping industry and the demand for accurate prediction of flowering time for R. pseudoacacia is increasing. In this study, we developed and compared performance of four different models predicting flowering time of R. pseudoacacia for the entire country: a Single Model for the country (SM), Modified Single Model (MSM) using correction factors derived from SM, Group Model (GM) estimating parameters for each region, and Local Model (LM) estimating parameters for each site. To achieve this goal, the bloom date data observed at 26 points across the country for the past 12 years (2006-2017) and daily temperature data were used. As a result, bloom dates for the north central region, where spring temperature increase was more than two-fold higher than southern regions, have advanced and the differences compared with the southwest region decreased by 0.7098 days per year (p-value=0.0417). Model comparisons showed MSM and LM performed better than the other models, as shown by 24% and 15% lower RMSE than SM, respectively. Furthermore, validation with 16 additional sites for 4 years revealed co-krigging of LM showed better performance than expansion of MSM for the entire nation (RMSE: p-value=0.0118, Bias: p-value=0.0471). This study improved predictions of bloom dates for R. pseudoacacia and proposed methods for reliable expansion to the entire nation.
Keywords: Robinia pseudoacacia; shift in flowering time; phenology model; site-specific model; local model
서 론
산업화 시대가 도래하면서 대기 중 온실가스 농도가 폭발적으로 증가함에 따라 전 지구적으로 기온이 급격히 상승하고 있다. 지구의 온도는 산업화 이전에 비해 1.5°C 상승하였고(IPCC, 2017), 1983~2012년 간 북반구 지표 온도는 과거 1400년의 기간 중 가장 높았던 것으로 평가되었다(IPCC, 2014). 북반구 중위도 지역에 위치하고 있는 우리 나라에서도 온난화 현상이 가속화되고 있다. 최근 30년(1988~2017년)간 기온은 20세기 초(1912~1941년)보다 약 1.4℃ 상승하였는데, 특히 겨울철(+2.1℃) 및 봄철(+1.9℃) 기온 상승이 두드러지게 나타났다(NIMS, 2018). 우리나라를 비롯하여 북반구에서 진행되고 있는 겨울 및 봄철의 기온 상승은 봄철 개화 수종들의 개화 시기를 앞당겼다(Menzel et al., 2006;Gonsamo et al., 2013; Ge et al., 2015; Templ et al., 2017). 온난화 현상에 대한 수목의 반응을 예측하기 위하여 온대 및 아한대 수종들을 대상으로 봄철 개화 현상을 모의하는 다양한 모형들이 활용되고 있지만(Linkosalo et al., 2008; Caffarra et al., 2011a; Caffarra et al., 2011b; Aguilera et al., 2015; Shi et al., 2017), 급격한 기온 상승과 더불어 기후변화의 영향으로 점차 빈발하는 이상 기상 현상은 봄철 개화 시기의 예측을 어렵게 한다(Blümel and Chmielewski, 2012; Chmielewski and Götz, 2016; Liu et al., 2018). 따라서, 앞으로 정확도 높은 봄철 개화시기 정보에 대한 수요가 더욱 증가할 것으로 판단된다.
온대지역에 분포하는 낙엽활엽수의 개화시기 예측에 있어서, 수목의 생리학적 메커니즘에 근거한 과정기반모형(process-based model)의 유용성이 입증되어왔다(Cesaraccio et al., 2004; Jung et al., 2005; Rea and Eccel, 2006; Matzneller et al., 2014; Yun et al., 2017; Kwon et al., 2020). 이러한 과정기반모형은 수목이 겨울에 겪는 휴면 과정을 모의하며, 여러가지 환경 요인의 영향으로 나타나는 개화 현상의 비선형적 반응을 반영한다(Basler, 2016). 늦여름에 새롭게 형성된 꽃눈은 가을이 시작되면서 낮아진 기온와 짧아진 광주기에 반응하여 내생휴면(endodormancy) 상태에 놓이게 된다(Lang et al., 1987; Horvath et al., 2003; Yu et al., 2020). 일정기간 저온 환경에 노출된 꽃눈은 내생휴면기를 지나 환경휴면기(ecodormancy)에 진입하게 되며, 생육에 적합한 환경(기온 상승, 광주기의 증가)이 조성되면 눈(bud)의 형태 형성(ontogenic development)이 촉진되고 파열(bud-burst)에 이르게 된다(Lang et al., 1987; Hänninen, 1990; Yu et al., 2020). 이 때 기온은 내생휴면 해제와 꽃눈 발달을 조절하는 가장 중요한 환경 인자로서(Campbell and Sorensen, 1973; Bertin, 2008; Harrington et al., 2010), 각각 겨울철 냉각온도(chilling temperature)의 축적과 봄철 생육촉진온도(forcing temperature)의 축적으로 모형에 반영된다. 국내에는 2000년대 초반, 겨울철 냉각온도의 축적을 고려하는 저온요구량모형(chilling and forcing model)이 최초로 도입되었으며 검증 결과, 개발된 모형은 기존에 보편적으로 사용되었던 선형회귀모형보다 뛰어난 성능을 보였다(Jung et al., 2005). 이후, 일기온자료를 바탕으로 저온요구량 모형을 활용하여 봄꽃, 작물들의 개화시기를 예측하는 연구들이 다수 수행되었다(Yun, 2006; Chung et al., 2009; Kim et al., 2013a; Kim et al., 2013b; Chun et al., 2016; Kim et al., 2020).
개화시기 예측에 있어 수종에 따라 도출한 과정기반모형이 갖는 큰 장점은, 여러 지역에서 관측된 개화일 자료와 환경 자료를 통합하여 지리적인 적용 범위가 넓은 모형을 도출하기 용이하다는 점이다(Basler, 2016; Pereira et al., 2018). 통합된 관측자료로부터 수종 특이적 모수가 결정되면, 각 지역에서 관측되는 환경 자료를 모형에 입력시켜 상세화된 지역별 예측이 가능하다. 그러나 이러한 통합 모형의 한계점 또한 분명히 존재한다. 동일한 종이라 할지라도 다른 기후 조건을 갖는 지역에 분포하는 수목은 오랜 시간 주변 환경에 적응하면서 가소성(phenological plasticity)을 보여(Tanino et al., 2010; Vitasse et al., 2013; Duputié et al., 2015; Ruml et al., 2016), 분포하고 있는 위도 또는 고도에 따라 수종별 모수 또한 변동성을 보일 수 있기 때문이다(Campoy et al., 2012). 따라서, 지역 단위 예측의 신뢰도 향상을 위해서는 지역적 특성이 추가적으로 반영된 모형을 개발하는 것이 필요하다.
전국적으로 5~6월에 걸쳐 개화하는 아까시나무는 우리나라에서 가장 중요한 밀원수종으로 손꼽히며, 아까시나무에서 생산되는 꿀은 국내 전체 꿀 생산의 70%에 이른다(Jun et al., 2016; Kohsaka et al., 2017; Jung and Lee, 2018). 하지만 최근 급격한 온난화 현상으로, 아까시나무의 개화시기가 앞당겨짐과 동시에 지역 간의 개화시기 간격이 단축되고 있다(NiFoS, 2016; NiFoS, 2017). 이러한 동시 개화 현상(simultaneous blooming)은 이동 양봉업자들의 채밀 활동을 어렵게 하고, 2010년대 들어서는 꿀 생산량이 점차 감소하는 등 양봉 산업에 큰 변화를 초래하였다 (Kohsaka et al., 2017; Jung and Lee, 2018). 따라서, 아까시나무 개화 시기의 지역별 변화 경향 파악과 함께 정확도 높은 개화시기 예측을 위한 모형 개발이 시급하다.
본 연구에서는 일기온 자료로 구동되는 과정기반모형을 활용하여, 아까시나무의 지역별 개화 시기 변화를 잘 설명할 수 있는 모형 개발을 목표로, 1) 시간에 따른 아까시나무 개화시기의 변화의 경향성을 권역별로 파악하고, 2) 수종 특이적 모형과 함께 지역적 특성을 함께 반영하는 서로 다른 세 모형을 개발, 성능을 비교 검증하였다.
재료 및 방법
1. 개화 및 기온 관측 자료
아까시나무 개화시기 예측 모형의 모수 추정 및 검증을 위해서 2006년부터 2017년까지 전국 각지에서 수집된 아까시나무의 만개일 자료를 활용하였다. 개화 관측은 매년 최남단 지역의 아까시나무 꽃이 만개한 시점에 해당 지역을 시작으로 북부 방향으로 이동하며 진행되었다. 조사지는 수평적 산지구분도에 근거하여 기후대별로 선정되었고, 그 지역을 대표할 수 있는 아까시나무 임분이 조사구로 선택되었다(가로수 및 공원수는 관측 대상에서 제외). 조사 지점마다 흉고직경 10~15 cm 사이의 건전한 평균목 5본이 관측대상목으로 지정되었으며, 남쪽으로 뻗은 가지 중에서 수관을 3등분 하였을 때 하부에 위치한 1차 가지를 대상으로 개화 상태가 측정되었다. 관측 시점에 측정된 개화 상태로부터 만개일을 추정하기 위하여 아까시나무의 전체 개화기를 7단계로 구분하였다(1단계: 꽃망울이 맺힌 상태, 2단계: 꽃망울이 벌어지기 직전 상태, 3단계: 꽃잎이 반 정도 열린 상태, 4단계: 꽃잎이 완전히 열린 상태, 5단계: 꽃잎이 변색하는 상태, 6단계: 꽃잎이 떨어지고 있는 상태, 7단계: 꽃잎이 완전히 떨어진 상태). 평년기온에서 한 단계는 약 2~3일간 지속되며, 전체 단계 중 만개기는 4단계에 해당된다. 관측 시 조사목마다 개화 단계를 측정한 후 평균 개화 단계를 계산하였으며, 이로부터 만개일을 역으로 추정하였다.
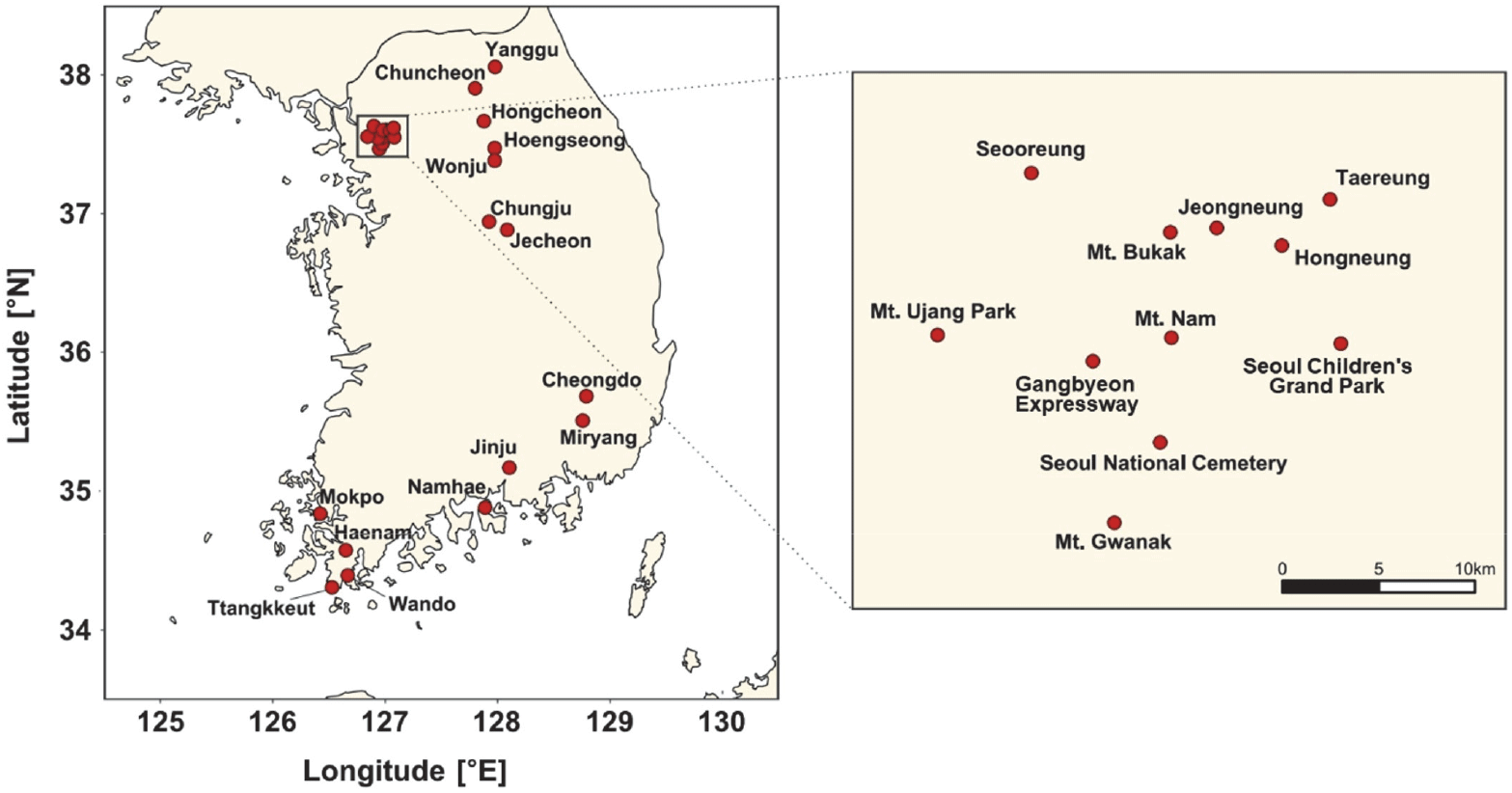
전체 조사지점 중, 결측년이 1년 이하인 남부 지역 8개소(목포, 땅끝, 해남, 완도, 남해, 진주, 밀양, 청도), 중북부지역 7개소(춘천, 홍천, 충주, 횡성, 원주, 양구, 제천), 서울 도심지역 11개소(우장산공원, 서오릉, 강변북로, 관악산, 현충원, 북악산, 남산, 정릉, 홍릉, 태릉역앞, 어린이대공원)에서 관측된 자료를 바탕으로, 지난 12년 간의 아까시나무 만개일의 변화 경향을 분석하고 만개일 예측을 위한 모형을 개발하였다. Table 1에 각 조사 지점의 경위도, 측정 고도 및 관측 기간 동안의 평균만개일을 수록하였으며, Figure 1에 해당 조사 지점들의 지리적 위치를 나타내었다.
Table 1.
Site information including geographic characteristics, winter (December, January, and February) and spring (March, April, and May) mean temperature, mean bloom dates (MBD), and standard deviation of bloom dates (SD) over the past 12 years (2006~2017). MUP: Mt. Ujang Park, GE: Gangbyeon Expressway, SNC: Seoul National Cemetery, SCGP: Seoul Children’s Grand Park.
| Site |
Longitude [°E] |
Latitude [°N] |
Elevation [m] |
Winter mean temperature [°C] |
Spring mean temperature [°C] |
MBD ± SD [DOY] |
| Mokpo |
126.4214 |
34.83606 |
18 |
2.93 |
12.40 |
135 ± 2.57 |
| Ttangkkeut |
126.5272 |
34.30667 |
124 |
2.70 |
12.23 |
136 ± 4.03 |
| Haenam |
126.6495 |
34.5726 |
34 |
2.19 |
11.98 |
135 ± 3.17 |
| Wando |
126.6666 |
34.39216 |
31 |
2.91 |
12.33 |
133 ± 4.37 |
| Namhae |
127.8893 |
34.87935 |
13 |
3.39 |
13.44 |
133 ± 4.37 |
| Jinju |
128.1044 |
35.1674 |
27 |
1.54 |
12.66 |
132 ± 4.50 |
| Miryang |
128.7572 |
35.5071 |
47 |
1.48 |
12.89 |
131 ± 4.79 |
| Cheongdo |
128.7891 |
35.68262 |
287 |
0.25 |
11.86 |
134 ± 3.55 |
| Chuncheon |
127.8002 |
37.90248 |
187 |
-3.85 |
10.15 |
139 ± 4.87 |
| Hongcheon |
127.8787 |
37.66586 |
156 |
-3.33 |
10.95 |
141 ± 5.20 |
| Chungju |
127.9241 |
36.94133 |
142 |
-3.24 |
10.23 |
136 ± 3.41 |
| Hoengseong |
127.9742 |
37.4713 |
118 |
-4.88 |
8.81 |
141 ± 7.79 |
| Wonju |
127.9742 |
37.38141 |
148 |
-3.15 |
10.47 |
139 ± 4.17 |
| Yanggu |
127.9778 |
38.05732 |
247 |
-4.75 |
8.81 |
150 ± 8.74 |
| Jecheon |
128.0849 |
36.88145 |
241 |
-3.46 |
9.79 |
139 ± 5.34 |
| MUP |
126.8434 |
37.55386 |
25 |
-1.98 |
10.84 |
137 ± 5.53 |
| Seooreung |
126.8986 |
37.62968 |
51 |
-1.60 |
11.29 |
141 ± 5.85 |
| GE |
126.9349 |
37.54162 |
5 |
-1.82 |
11.15 |
135 ± 5.18 |
| Mt. Gwanak |
126.9476 |
37.46609 |
58 |
-3.96 |
8.77 |
139 ± 5.01 |
| SNC |
126.9745 |
37.50365 |
31 |
-2.61 |
10.28 |
136 ± 5.13 |
| Mt. Bukak |
126.9806 |
37.60198 |
268 |
-2.27 |
10.56 |
143 ± 6.97 |
| Mt. Nam |
126.9812 |
37.55262 |
118 |
-1.87 |
11.21 |
137 ± 4.42 |
| Jeongneung |
127.0078 |
37.60397 |
91 |
-2.23 |
10.61 |
137 ± 5.05 |
| Hongneung |
127.0462 |
37.59579 |
68 |
-1.70 |
11.21 |
137 ± 5.48 |
| Taereung |
127.0746 |
37.61732 |
21 |
-1.84 |
11.09 |
133 ± 5.26 |
| SCGP |
127.0809 |
37.5499 |
31 |
-1.88 |
11.07 |
133 ± 4.89 |
Download Excel Table
Figure 1.
Geographical locations of 26 site, where the flowering of Robinia pseudoacacia was observed.
Download Original Figure
아까시나무 개화 관측 지점의 일기온정보를 추정하기 위해 1 km 해상도로 상세화된 과거 일기온 복원자료를 활용하였다. 해당 자료는 종관기상관측시스템(Automated Surface Observing System, ASOS), 방재기상관측시스템(Automatic Weather System, AWS), 산악기상관측시스템으로(Automatic Mountain Meteorology Observation System, AMOS)에서 관측된 기온정보를 융합하여 공간 분석을 수행한 후, 일별 기온 3요소(일최고기온, 일평균기온, 일최저기온)를 래스터 정보로서 산출한 자료이다. 공간 분석은 역거리 가중치법(Inverse Distance Weighting Method, IDW Method)을 바탕으로 하였으며, 고도편차에 의한 일별 기온감률을 적용하였다(Yun et al., 2001). 개화 관측 지점이 위치한 격자에서 일별 최고기온, 평균기온, 최저기온 정보를 추출하였다. 땅끝과 해남 지점은 산출된 래스터 자료의 격자 범위 외부에 위치하므로, 두 지점의 경우 실제 관측 지점와 가까우면서도 고도가 비슷한 범위 내에 있는 격자를 선택, 해당 격자에서 일기온 정보를 추출하였다. 전체 관측 기간 동안의 지점별 겨울철(12~2월) 평균 기온 및 봄철(3~5월) 평균기온을 Table 1에 나타내었다. 남부지역의 조사 지점 중 목포와 땅끝, 완도, 남해는 해안으로부터의 거리가 1 km 이내에 불과하며, 겨울철 평균기온은 2℃ 이상, 봄철 평균온도는 12℃ 이상으로 다른 지점보다 상대적으로 기온이 높았다. 중북부 지역의 경우, 모든 관측 지점들은 해발고도가 100 m 이상으로 다른 지역보다 상대적으로 높은 지대에 위치하고 있으며 낮은 기온 분포를 보였다(Table 1).
Table 2.
Functions and equations used in process-based model (Cesaraccio et al., 2004; Cesaraccio et al., 2005) to predict bloom dates. t2: bloom date, t1: start date of forcing accumulation, t0: start date of endodormancy; Rc: chilling rate, Rf: forcing rate, Sc: state of chilling, Sf: state of forcing, C*: chilling requirement, F*: forcing requirement, TB: base temperature, Tx: daily maximum temperature, Tm: daily mean temperature, Tn: daily minimum temperature.
| Equation |
|
|
|
|
|
|
|
Download Excel Table
2. 모형 설계
본 연구에서 활용한 식물계절모형은 Cesaraccio et al. (2004)이 제안한 저온요구량모형(Chill days model)이다. 이 모형은 온대 낙엽수의 겨울철 휴면생리에 근거한 과정기반모형으로 내생휴면과 환경휴면 두 단계의 휴면 과정을 모의한다. 모형에 의하면, 겨울철 냉각온도의 적산량이 저온요구량(Chilling requiremnet)에 도달하면 내생휴면이 해제되고 그 이후, 생육촉진온도의 적산량이 같은 크기의 임계값에 도달하면 환경휴면이 타파되고 눈(bud)은 생장을 재개한다(2단계 순차휴면모형, Sequential model). 냉각온도 및 생육촉진온도의 적산률은 단일삼각도일 계산법(Single triangle degree day calculation, 단위: °D(degree days))으로 구하였다(Table 2).
아까시나무 만개일 모형의 모수는 내생휴면 시작일과 저온요구량, 기준온도, 고온요구량(Heating requirement)이다. 고온요구량은 내생휴면이 해제된 후 꽃이 만개하기까지 생육촉진온도의 총 적산량으로 정의하였다. 온대 낙엽수목이 휴면을 시작하는 시점은 직접 관측이 불가능하므로, 대부분의 저온요구량모형에서 휴면 시작일은 가을철 식물계절현상이 시작되는 날짜(Cesaraccio et al., 2004), 임의로 가정한 특정한 날짜 등으로 대체된다(Jung et al., 2005; Matzneller et al., 2014; Chmielewski and Götz, 2016). 본 연구에서는 10월 1일을 휴면의 시작점으로 가정하였으며, 결과적으로 휴면 시작일을 제외한 저온요구량, 기준온도, 고온요구량을 모형의 모수로서 추정하였다.
12년 동안의 만개일 자료는 년도별로 7:5 또는 6:5의 비율로 나누어 각각 모수 추정을 위한 자료(훈련자료, calibration dataset)와, 개발 모형의 성능을 검증하는 자료(검증자료, validation dataset)로서 활용하였다. 모형의 과적합을 최소화하기 위하여 자료의 분리는 무작위적으로 이루어졌으며, Wilcoxon 순위합 검정을 시행하여 최종적으로 유사한 분포를 갖는 두 집단으로 분리하였다(Gehan, 1965; Bogawski et al., 2019; Liu et al., 2019). 결과적으로 2006, 2008, 2009, 2010, 2015, 2016, 2017년의 만개일 자료를 모수 추정에 사용하였고, 그 외의 자료는 모형 검증에 사용하였다.
모수 추정에 R 패키지 GenSA를 활용(Xiang et al., 2013), 최적화 과정에 담금질 기법(generalized simulated annealing)을 적용하였다(Chuine et al., 1998; Kalvans et al., 2015; Roberts et al., 2015). 알고리즘 적용에는 모수의 최적화 범위를 설정하는 단계가 선행되어야 한다. 최적화 범위가 주어지면, 예측 만개일과 관측 만개일의 평균제곱근오차(Root mean squared error, RMSE)가 최소가 되는 모수 추정치가 해당 범위 내에서 결정된다. 저온요구량, 기준온도, 고온요구량의 최적화 범위는 각각 -200 이상 -40 이하(단위: °D), 2 이상 15 이하(단위: ℃), 40 이상 600 이하(단위: °D)로 설정하였다. 모형마다 난수의 씨앗(seed) 값을 1부터 30까지 지정하여 30번 담금질 과정을 시행하였으며, 가장 낮은 RMSE를 갖는 모수 조합을 최적 모수로 선택하였다.
또한, 전 지역에 대해 단일 모수를 추정하는 전국 통합 모형(Single Model, SM)과 전국 통합 모형에 지점별 보정계수를 도입한 수정된 통합 모형(Modified Single Model, MSM), 권역 내에서 단일 모수를 추정하는 권역별 통합 모형(Group Model, GM), 관측 지점마다 개별적으로 모수를 추정하는 개별 지역 모형(Local Model, LM)까지 총 4가지 방식으로 모수를 추정, 모형을 개발하였다. 수정 통합 모형은 전국 통합 모형의 기준온도와 저온요구량, 고온요구량의 추정값과 동일한 값을 이용하여 각 지점의 만개일을 계산한 후, 지점별 보정계수 값을 합하였다. 수정 통합 모형의 보정계수는 전국 통합 모형에서 훈련자료를 대상으로 계산된 만개일의 지점별 편의(Bias) 값에 음의 부호를 취하여 각 지점별 보정계수로 정의하였다.
3. 모형 평가
모형의 성능을 평가하기 위하여 평균제곱근오차(Root mean square error, RMSE) 편의(Bias), 피어슨 상관계수(Pearson correlation coefficient, r)의 지표를 사용하였다. 피어슨 상관계수는 프로그래밍 언어 R의 기본 패키지에 내장되어 있는 cor 함수를 활용하였다. 이를 바탕으로 훈련자료와 검증자료에 대한 전국 통합 모형, 수정된 통합 모형, 권역별 통합 모형, 개별 지역 모형의 성능을 비교하였다.
N:분석기간 동안의 관측년도 수
d pi:i 번째 년도의 예측 만개일
d oi:i 번 째 년도의 관측 만개일
d oi:분석기간 동안의 평균 관측 만개일
4. 통계 분석
만개시기에 영향을 크게 미치는 기간을 탐색하기 위해 26개 관측 지점을 대상으로 12년 간의 만개일과 월별 평균기온의 상관관계를 조사하였다. 그 결과, 12개 지점에서는 4월 평균기온이, 그 외 11개 지점에서는 3월 평균기온이 만개일과 가장 높은 상관계수를 보였다(p-value<0.05). 이에 따라, 26개 관측 지점의 과거 12년 간(2006년~2017년)의 만개일의 변화와 3, 4월 평균기온의 변화 경향을 권역별로 구분하여 분석하였다. 권역별 구분 기준은 지점별 일평균기온의 상관관계를 바탕으로 계층적 군집화를 통해 4개 권역으로 분류하였다(남서부(목포, 땅끝, 해남, 완도), 남동부(남해, 진주, 밀양, 청도), 중북부(춘천, 홍천, 충주, 횡성, 원주, 양구, 제천), 서울 도심(우장산공원, 서오릉, 강변북로, 관악산, 현충원, 북악산, 남산, 정릉, 홍릉, 태릉역앞, 어린이대공원)). 또한, 시간의 흐름에 따라 권역 간 만개일의 차이가 어떻게 변화하는지 조사하였다. 통계 분석법으로 맨-켄달 경향 분석법(Mann-Kendall trend test)을 이용하였으며(Xiang et al., 2013), R 패키지 zyp와 wql를 활용하였다.
모형 선택을 위해 각 모형별로 전체 지역에 대한 모형 성능, 권역별 모형의 성능, 26개 관측 지점의 오차(RMSE, 편의) 분포를 비교하였다. 오차의 분포 형태가 모형 간에 차이를 보이는지 검정하기 위하여 일원배치 분산분석(One-way ANOVA)을 수행하였으며, 모형 간 차이가 통계적으로 유의한 경우 사후분석으로 Tukey 검정(Tukey's test)을 시행하였다. 또한, Student의 T 검정법(Student’s T test)을 이용, 오차의 분포에 있어 훈련자료와 검증자료 사이에 통계적으로 유의미한 차이가 존재하는지 확인하였다. 비교해야하는 집단 간의 분포가 등분산성을 만족하지 못하는 경우, 비모수 검정법을 활용하였다(Kruskal-Wallis 검정, Wilcoxon 순위합 검정)(Chuine et al., 1998; Kalvans et al., 2015; Roberts et al., 2015). 모든 통계 분석은 프로그래밍 언어 R로 수행하였다.
결 과
1. 만개일 변화 경향
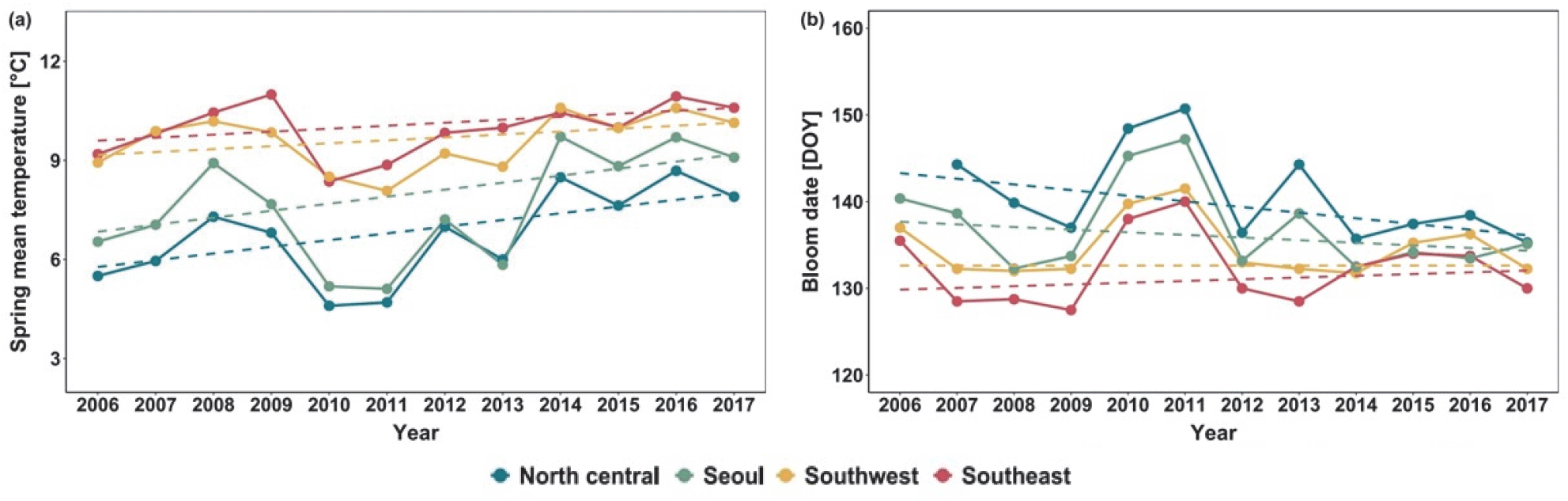
과거 12년(2006년~2017년)동안의 아까시나무 만개일의 변화 및 봄철(3~4월) 평균 기온의 변화 경향을 4개 권역별로 분석하였다(Table 3, Figure 2). 분석 기간 동안 봄철 평균기온은 모든 지역에서 상승하는 경향을 보였다[Table 3(a), Figure 2(a)]. 서울 도심지역의 봄철 기온 변화의 기울기(Sen’s slope)는 0.2123℃/yr로 전체 지역 중 가장 컸으며, 분석 기간 중 기온이 가장 높았던 2014년 3, 4월 평균기온(9.72℃)은 기온이 가장 낮았던 2011년 3, 4월 평균기온(5.11℃)에 비해 4℃ 이상 높은 값을 나타냈다. 중북부 내륙 지역의 경우, 기온 변화의 기울기(Sen’s slope)는 0.2033℃/yr로 전체 지역 중 서울 도심 다음으로 두번째로 컸으며, 통계적으로 유의한 기온 증가 추세를 보였다(p-value=0.0327). 한편, 남서부 및 남동부 지역은 기온 변화의 기울기가 다른 두 지역의 50% 이하 수준으로 낮게 나타났으며, 특히 남서부 해안지역은 네 지역 중 기온 변화가 가장 적었다(Sen’s slope=0.0886℃/yr).
Table 3.
Mann–Kendall test statistics for time-series trends (a) in spring (March and April) temperature and bloom dates for Robinia pseudoacacia, (b) The difference in mean full bloom dates between regions. Sen’s slope: temperature change per year.
| (a) |
| Region |
Spring temperature |
Bloom dates |
| Sen’s slope [°C/yr] |
Mann–Kendall statistic [τ] |
P(<τ) |
Sen’s slope [days/yr] |
Mann–Kendall statistic [τ] |
P(<τ) |
| Southwest |
0.0886 |
20 |
.2464 |
0 |
-2 |
.9442 |
| Southeast |
0.0905 |
30 |
.0769 |
0.2000 |
6 |
.7305 |
| North central |
0.2033 |
36 |
.0327 |
-0.6508 |
-20 |
.1379 |
| Seoul |
0.2123 |
26 |
.1272 |
-0.3028 |
1-9 |
.5824 |
| (b) |
| Region-Region |
Sen’s slope [days/yr] |
Mann–Kendall statistic [τ] |
P(<τ) |
| Southwest-Southeast |
-0.1056 |
-14 |
0.3704 |
| Southwest-North central |
-0.7098 |
-27 |
0.0417 |
| Southwest-Seoul |
-0.0336 |
-3 |
0.8907 |
| Southeast-North central |
-1.0119 |
-26 |
0.0509 |
| Southeast-Seoul |
-0.4670 |
-17 |
0.2714 |
| North central-Seoul |
-0.2251 |
-19 |
0.1585 |
Download Excel Table
Figure 2.
Changes of mean temperature in spring (March and April) and (b) the bloom dates of Robinia pseudoacacia by region over the past 12 years (2006~2017).
Download Original Figure
만개일의 변화 경향은 봄철 평균기온의 변화 경향과 달리 지역에 따라 상반된 양상을 보였다[Table 3(a), Figure 2(b)]. 만개일은 중북부 내륙 지역과 서울 도심 지역에서 점차 앞당겨지는 경향을 보인 반면(Sen’s slope<0), 남부 지역에서는 관측 기간 동안 만개일 변화의 방향성이 뚜렷하게 나타나지 않았고, 남동부 지역에서는 오히려 변화의 기울기가 양의 값을 갖는 것으로 나타났다. 하지만 이러한 지역별 만개일 변화의 경향성은 관측 기간 내 만개일의 큰 연별 변화(annual variation)로 인해 통계적으로 유의하지는 않았다.
결과적으로, 지난 12년 동안 지역 간의 만개일 차이는 점차 감소하였다[Table 3(b), Figure 2(b)]. 중북부 내륙 지역과 남서부 해안 및 남동부 지역의 평균 만개일 차이는 분석 기간 동안 매년 0.7일 이상의 속도로 줄어들었는데, 이는 중북부 내륙 지역의 급격한 봄철 기온 상승에 의한 것으로 판단된다. 특히 남서부 해안 지역과 중북부 내륙 지역의 평균 만개일 차이는 12년의 비교적 짧은 기간에도 통계적으로 유의미한 감소를 보였다(p-value=0.0417). 2007년, 중북부 지역과 남서부 해안 지역의 평균 만개일은 각각 144.29 DOY(Day Of Year), 132.25 DOY로 두 지역간의 만개일은 평균적으로 12일 정도의 차이를 보였으나, 2014년 이후부터 두 지역 간의 평균 만개일 차이는 4일 이하로 지속되었다. 중북부 내륙 지역과 남동부 지역의 경우도, 2011년 까지 평균 만개일 차이가 10일 내외로 유지되었으나, 최근 들어 급격히 줄어드는 양상을 보였다. 2007년, 15.78일까지 차이를 보였던 두 지역의 평균 만개일은 2014년에 불과 3.21일만의 차이를 나타냈고, 2014년부터 2017년까지 3~5일 정도의 차이를 유지하였다.
2. 추정 모수
여러 지역을 대상으로, 보다 정확도 높은 개화시기 예측을 위해 서로 다른 4가지 방식으로 모수를 추정하였다. 전 지역에 대해 단일 모수를 추정하는 SM에서 최적의 기준온도와 저온요구량, 고온요구량은 각각 8.88℃, -138.95 °D, 247.73°D로 결정되었다. 그리고 SM에 지점별 보정계수를 도입한 MSM, 권역 내에서 단일 모수를 추정하는 GM, 관측 지점마다 개별적으로 모수를 추정하는 LM에서 추정된 모수를 Table S1에 나타내었다.
MSM에서 지역별 보정계수는 대략 -11에서 7까지의 분포를 나타냈다. 양의 부호를 갖는 보정계수 중 절대값이 가장 컸던 지점은 남해였으며(보정계수=7.1429), 음의 부호를 갖는 보정계수 중 절대 값이 가장 컸던 지점은 관악산이었다(보정계수=-11.1429). 이는 SM이 남해 지점에서 만개일을 실제보다 7일 정도 빠르게, 관악산 지점에서 만개일을 실제보다 11일 정도 느리게 예측한다는 것을 의미한다. 남부지역의 경우 보정계수는 모두 0보다 컸으며, 남해를 포함하여 진주와 밀양은 5 이상의 보정계수 값을 가졌다.
GM에서, 서울 도심지역 및 남서부 지역은 기준온도가 5℃ 가까이 크게 감소하였고, 그와 동시에 고온요구량의 크기는 2배 이상 증가하였다. 남동부 지역은 모든 지역 중 추정 모수의 변화가 가장 적었다. 한편 LM 방식으로 추정된 모수는 지점별로 다양한 분포를 보였다.
3. 모형별 성능 비교
1) 전체 지역 및 권역별 모형 성능
훈련자료와 검증자료에 대한 SM, MSM, GM, LM의 성능을 전체 지역에 대해 비교한 결과와 권역별로 비교한 결과를 Table 4에 나타내었다. 전체 지역에 대한 모형 성능은 SM 및 GM보다 MSM, LM이 더 우수했다. 훈련 자료에 대한 성능은 LM이(RMSE=3.09, r=0.88), 검증 자료에 대한 성능은 MSM이(RMSE=4.62, r=0.82) 가장 뛰어났다. 다만 LM의 경우, 훈련자료에 다소 과적합된 경향을 보였다. LM의 검증 결과에서, 훈련 결과 대비 RMSE는 2일 이상 증가하였으며 상관계수는 0.1 이상 감소하였는데, 이는 모든 모형 중 가장 큰 성능 격차를 나타낸다. 전체 지역에 대한 SM의 RMSE는 모든 모형 중 가장 컸으며, SM에 비해서 MSM은 24% 이상, LM은 15% 이상 감소한 RMSE 값을 나타냈다.
Table 4.
Performance of Single Model (SM), Modified Single Model (MSM), Group Model (GM), and Local Model (LM) by region for calibration and validation dataset. (a) Root mean square error (RMSE), (b) Bias, (c) Pearson’s correlation coefficient (r).
| (a) |
| Region |
Model |
| SM |
MSM |
GM |
LM |
| RMSEcal |
RMSEval |
RMSEcal |
RMSEval |
RMSEcal |
RMSEval |
RMSEcal |
RMSEval |
| Southwest |
4.88 |
4.06 |
3.32 |
4.60 |
2.79 |
4.64 |
2.14 |
4.76 |
| Southeast |
6.16 |
6.62 |
3.27 |
6.12 |
3.89 |
6.15 |
2.23 |
5.48 |
| North central |
6.21 |
5.09 |
3.80 |
3.49 |
5.69 |
4.57 |
3.06 |
4.40 |
| Seoul |
6.49 |
7.05 |
4.35 |
4.63 |
6.09 |
6.20 |
3.64 |
5.63 |
| Total |
6.13 |
6.11 |
3.90 |
4.62 |
5.25 |
5.57 |
3.09 |
5.17 |
| (b) |
| Region |
Model |
| SM |
MSM |
GM |
LM |
| Biascal |
Biasval |
Biascal |
Biasval |
Biascal |
Biasval |
Biascal |
Biasval |
| Southwest |
-3.32 |
-0.95 |
-7.31×10-14 |
2.37 |
-0.43 |
0.95 |
-0.14 |
1.70 |
| Southeast |
-4.75 |
-2.60 |
-1.52×10-14 |
2.15 |
-0.04 |
1.55 |
0.11 |
1.35 |
| North central |
1.79 |
2.06 |
1.42×10-14 |
0.27 |
0.48 |
0.69 |
-0.43 |
-0.20 |
| Seoul |
1.81 |
4.53 |
-9.74×10-14 |
2.70 |
-0.24 |
1.78 |
-0.20 |
2.60 |
| Total |
-0.10 |
1.92 |
-1.93×10-14 |
1.91 |
-0.06 |
1.32 |
-0.20 |
1.52 |
| (c) |
| Region |
Model |
| SM |
MSM |
GM |
LM |
| rcal |
rval |
rcal |
rval |
rcal |
rval |
rcal |
rval |
| Southwest |
0.62 |
0.51 |
0.69 |
0.54 |
0.72 |
0.56 |
0.85 |
0.56 |
| Southeast |
0.76 |
0.19 |
0.79 |
0.15 |
0.75 |
0.21 |
0.87 |
0.25 |
| North central |
0.60 |
0.79 |
0.83 |
0.89 |
0.64 |
0.80 |
0.89 |
0.82 |
| Seoul |
0.67 |
0.70 |
0.83 |
0.86 |
0.68 |
0.63 |
0.86 |
0.76 |
| Total |
0.70 |
0.74 |
0.83 |
0.82 |
0.71 |
0.72 |
0.88 |
0.77 |
Download Excel Table
모형별 성능을 권역별로 비교한 결과에 의하면(Table 4, Figure S1), 남동부 지역의 경우 훈련 및 검증 자료 모두에서 LM의 성능이 가장 우수한 것으로 나타났으며, 가장 좋지 못한 성능을 보인 모형은 SM이였다. 훈련 결과, LM(RMSE=2.23)에서 RMSE는 SM(RMSE=6.16)에 비해 47% 가까이 감소한 값을 나타냈으며, 상관계수는 SM(r= 0.76)에 비해 LM(r=0.87)에서 0.11 만큼 증가하였다. 남서부 지역의 경우 훈련 결과에 있어서는 남동부 지역과 유사하게, LM이 가장 낮은 RMSE와 가장 높은 상관계수를 갖는 것으로(RMSE=2.14, r=0.85), SM이 가장 높은 RMSE와 가장 낮은 상관계수를 갖는 것으로 나타났다(RMSE=4.88, r=0.62). 다만 검증 결과에서 네 모형은 모두 비슷한 성능을 보였는데, 남서부 해안 지역에서 네 모형 간의 RMSE 차이는 모두 1일 이하, 상관계수 차이는 0.05 이하로 나타났다. 중북부 내륙 및 서울 도심 지역 모두 훈련 자료에서는 LM의 성능이, 검증 자료에서는 MSM의 성능이 가장 좋았다. 또한 훈련 및 검증 자료 모두에서 SM은 가장 성능이 떨어지는 경향을 보였다. 훈련 결과, 두 지역 모두에서 LM과 MSM은 SM 대비 RMSE가 33% 이상 감소하였고 상관계수는 0.2 가까이 또는 그 이상 증가하였다. 검증 결과에서도 LM과 MSM은 SM 대비 더 향상된 성능을 보였는데, LM에서는 10% 이상, MSM에서는 30% 이상의 RMSE 감소율을 나타냈다.
2) 지점별 오차 분포
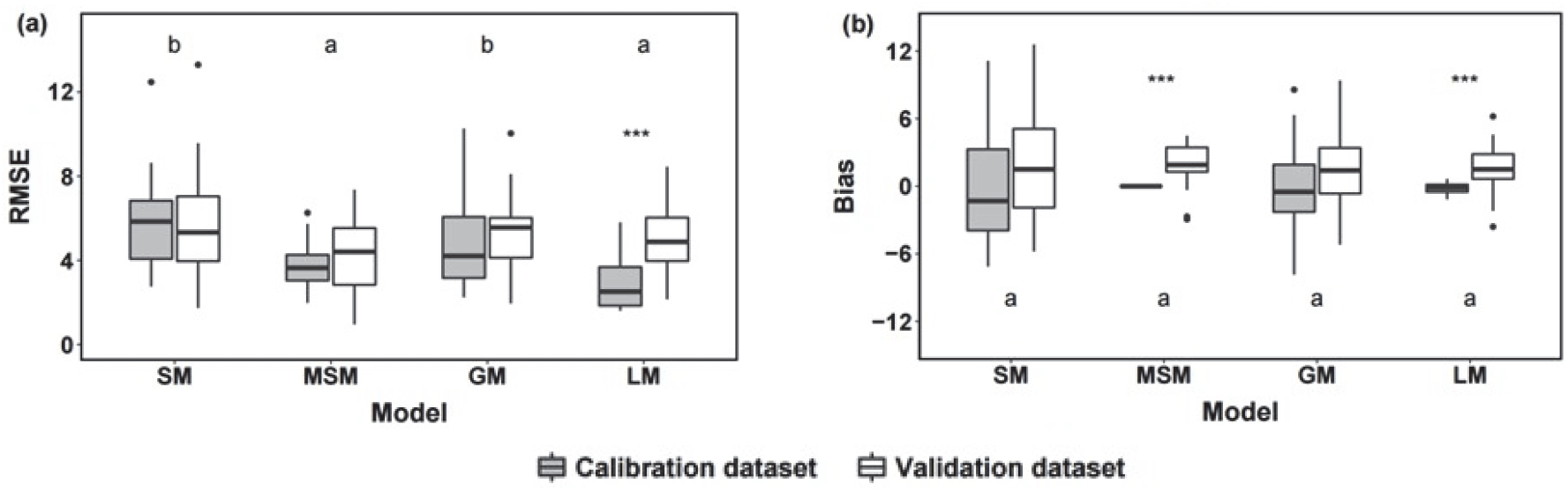
서로 다른 네 모형(SM, MSM, GM, LM) 별로 전국 26개 관측 지점의 오차(RMSE, 편의)를 비교하였다(Figure 4, Table S2). MSM과 LM은 SM 및 GM보다 낮은 RMSE 분포를 나타냈으며[Figure 4(a)], 통계적으로 유의한 차이를 보였다(p-value=1.315×10-6). LM의 경우 26개 관측 지점의 평균 RMSE는 훈련자료에서 2.83, 검증자료에서 4.94로 나타났으며, 전체 모형 중 유일하게 훈련 및 검증 자료 간 RMSE 분포가 통계적으로 유의하게 달랐다(p-value=1.522×10-6). 이는 개별 지역 모형이 훈련 자료에 과적합된 것을 보여주는 결과이다. 한편, 26개 지점별 편의의 분포를 살펴보았을 때, SM이나 GM보다 MSM과 LM에서 전체 분포 범위가 좁게 나타났다[Figure 4(b)]. 편의의 산포도는 MSM에서 가장 작았고, SM에서 가장 컸다. 특히 검증 자료에서, 편의의 표준편차는 수정 통합 모형이 1.98, 개별 지역 모형이 2.12로 SM보다 2배 이상 낮은 값을 나타냈다. RMSE 분포와 마찬가지로, LM의 관측 지점별 편의 분포는 훈련 및 검증 자료 간에 통계적으로 유의한 차이를 보였다(p-value= 1.154×10-4). 또한 MSM 역시 훈련, 검증 자료에서 나타난 편의의 분포가 유의하게 달랐는데(p-value=1.897×10-5), 이는 MSM에서 보정계수를 도출할 때, 모형의 훈련 성능 지수로서 산출된 지점별 편의 값을 그 지점에 대한 보정계수로 설정함으로써, 훈련 자료에 대한 모든 지점별 편의를 0에 가깝게 만들었기 때문이다.
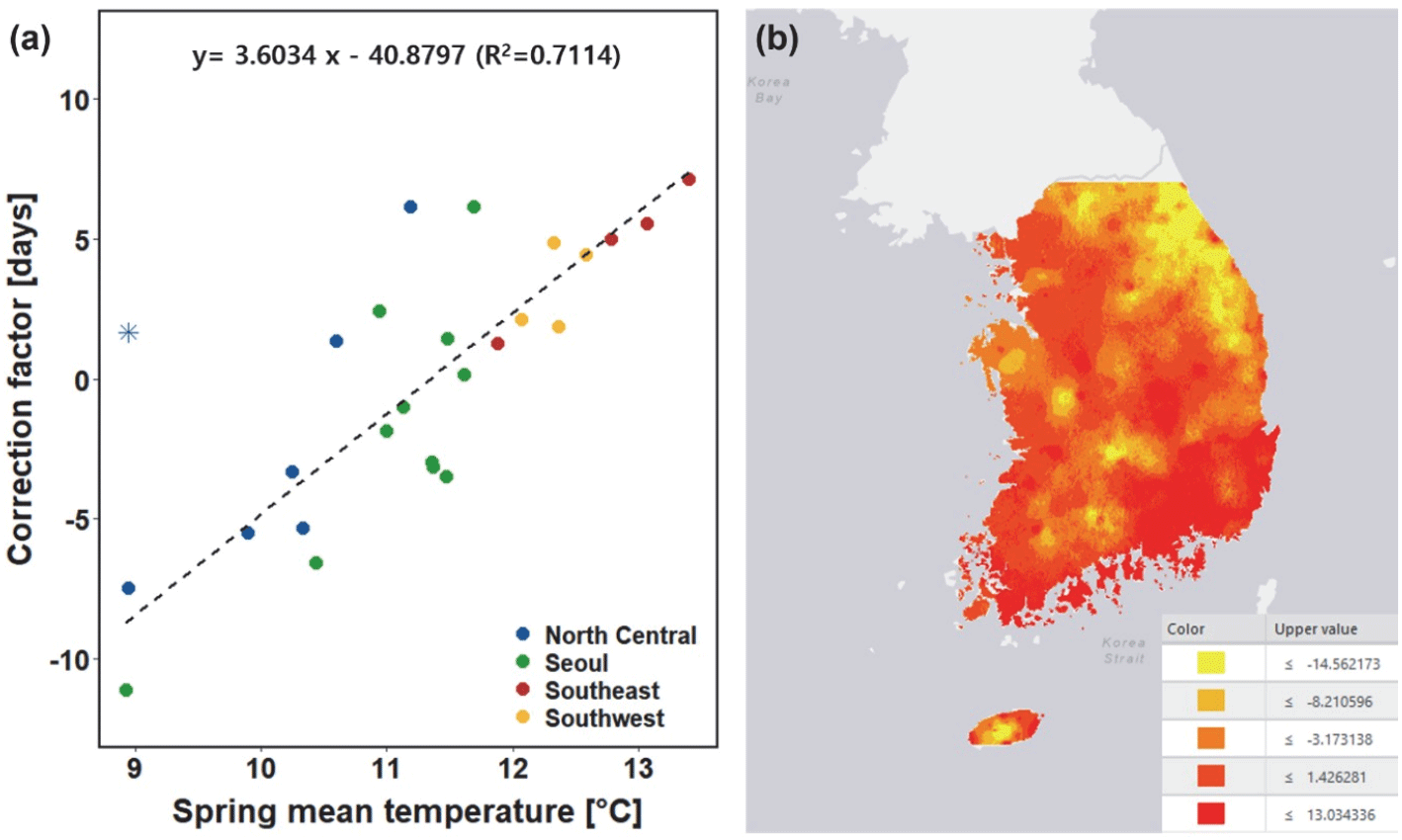
Figure 4.
(a) Regression between spring (March, April, and May) mean temperature and correction factor used in Modified Single Model (MSM), and (b) distribution map of the correction coefficients calculated from the regression equation.
Download Original Figure
Figure 3.
Boxplots of RMSE and Bias of 26 sites by 4 types of models (SM, MSM, GM, LM). Different letters indicate significant differences in model performance. The difference between calibration and validation error were presented as ‘*’, ‘**’, and ‘***’at 0.05, 0.01 and 0.001 level, respectively. SM: Single Model, MSM: Modified Single Model, GM: Group Model, LM: Local Model, RMSE: Root mean square error.
Download Original Figure
고 찰
1. 봄철 기온 및 만개일의 변화 경향
본 연구에서는 지난 12년(2006~2017년)동안 관측된 아까시나무 만개일 자료를 활용하여 최근 들어 더욱 심화되고 있는 온난화로 인해 아까시나무의 개화 시기가 어떻게 변화하고 있는지 살펴보았다. Figure 2에 나타난 바와 같이, 시간에 따른 권역별 만개일의 변화 경향은 봄철(3, 4월) 기온의 변화 경향과 상응한다. 봄철 기온이 증가하면 만개일은 빨라지는 음의 상관관계를 보이며(Figure S2), 이러한 변화 경향은 분석 기간 동안 4개 권역에서 일치한다.
아까시나무 만개일의 변화 경향을 권역별로 조사한 결과에 따르면(Table 3), 봄철(3, 4월) 기온 상승률이 낮았던 남부 지역에서는 아까시나무의 만개일 변화 경향성이 뚜렷하게 나타나지 않은 반면, 남부 지역보다 2배 이상 높은 봄철 기온 상승률을 보였던 중북부 내륙 지역은 분석 기간 동안 네 지역 중 가장 빠른 속도로 만개일이 앞당겨졌다(Sen’s slope=-0.6508 days/yr). 그 결과 남부 지역과 중북부 지역에서 아까시나무가 만개하는 시기의 간격이 크게 단축 되었으며, 특히 남서부 해안 지역과 중북부 내륙 지역의 평균 만개일 차이는 통계적으로 유의하게 감소하였다(p-value=0.0417). 이와 유사하게, 봄철 개화종 7종을 대상으로 국내 14개 지점에서 관측된 개화일의 장기(1945~ 2007년) 시계열 변화를 분석한 선행 연구 결과에서, 해안 지역보다 내륙 지역의 봄철 식물계절 시기가 더 빠른 속도로 앞당겨져 해안, 내륙 지역간 개화일 차이가 줄어들었음이 밝혀졌다(Lee et al., 2009). 국외에서도 지역간 불균형한 기온 상승으로 인해 봄철 식물계절 시기의 지리적 변동이 감소한 사례가 보고된 바 있다. Ma et al.(2018)은 유럽에 분포하고 있는 온대 수종 16종의 1980~2013년 개화, 개엽 시기와 겨울 및 봄철 기온을 분석하여, 기온이 낮은 지역에서 온난화가 더욱 빠르게 진행되어 따뜻한 지역보다 개화, 개엽 시기가 더 앞당겨졌다는 사실을 확인하였다. 또한 Vitasse et al.(2018)은 고도가 다른 알프스 128개 지역에서 1960~2016년에 걸쳐 4수종의 개엽 시기가 어떻게 변화하는지 조사하였는데, 그 결과 고도가 높을수록 개엽 시기가 더 크게 앞당겨졌음이 드러났고, 이는 겨울과 늦은 봄의 높은 기온 상승으로 인한 것이라고 주장하였다.
한편, 서울 도심 지역의 경우 시간에 따른 봄철 평균 기온 및 만개일의 맨-켄달 경향 분석결과, 기온의 변화율은 0.2123℃/yr로 네 지역중 가장 높았던 반면, 만개일의 변화율은 -0.3028 days/yr로 중북부지역에 비해 50% 이상 낮았다(Table 3). 즉 서울의 3, 4월 기온 상승률은 중북부지역보다 높았지만 만개일의 변화율은 비교적 낮았고, 그 결과 남부 지역과의 만개일 차이 또한 크게 감소하지 않았다. 이는 중북부 내륙 지역이 다른 지역에 비해 아까시나무가 개화하는 시기가 늦어[Figure 2(b)], 개화 직전 및 개화 후 만개에 이르기까지의 기간인 5월 중의 기온 또한 중북부 지역의 만개 시기에 큰 영향을 미치기 때문인 것으로 판단된다. 실제로 분석 기간 중 중북부 지역의 평균 만개일은 140.71일(±6.96)로 서울 도심(137.09±5.93) 지역이나 남서부(134.63±3.61) 및 남동부(132.25±4.33) 지역에 비해 만개 시기가 평균적으로 4~8일 가량 늦었다. 특히 양구에서는 2009년, 2017년을 제외한 모든 년도에서 5월 25일 이후 만개한 것으로 관측되었으며, 2010년과 2011년에는 중북부 내륙 지역에 속하는 7개 지점 모두 5월 20일 이후에 아까시나무가 만개한 것으로 관측되었다. 또한, 맨-켄달 경향 분석을 통해 2006~2017년 간 5월 평균기온의 변화 경향을 권역별로 살펴보았을 때, 네 지역 모두에서 통계적으로 유의한 온도 상승이 나타났는데, 그 중 중북부 내륙 지역의 기온 상승률이 가장 높았다(중북부: +0.2027℃/yr (p-value=0.0019), 서울 도심: +0.1732℃/yr (p-value=0.0240), 남동부: +0.1030℃/yr (0.0240), 남서부: +0.1255℃/yr (p-value= 0.0087)).
우리나라의 기후변화 특성을 분석한 결과에 따르면(NIMS, 2018), 과거 106년(1912~2017년) 동안의 계절별 기온 상승률은 겨울(+0.25℃/10년), 봄(+0.24℃/10년), 가을(+0.16℃/10년), 여름(+0.08℃/10년) 순으로 높았으나, 최근 10년(2008~2017년) 동안 겨울철 기온 상승이 둔화되어 겨울 이외의 계절의 기온 상승이 더 뚜렷하게 나타났다. 또한 기온의 월별 변화를 보았을 때, 최근 30년(1988~2017년)에 비해 최근 10년 간의 기온은 5~8월에 상승, 12~1월에 하강, 2~4월에는 큰 차이가 없는 것으로 드러났다. 본 연구 결과에 의하면, 지역에 따라 5월 초에서 6월에 걸쳐 개화하는 아까시나무는 최근 12년(2006~2017년) 간의 짧은 관측 기간에도 불구하고 일부 지역 간의 만개일 변이가 크게 감소하였으며, 2014년 이후부터 이러한 양상이 더욱 심화되었다[Figure S3(a)]. 이러한 연구 결과는 앞서 언급했던 국내 기온 변화의 최근 동향이 반영된 것으로 보인다. Lee et al.(2014)는 1951~1980년, 1981~2010년 두 기간 동안 국내 6개 지역에서 관측된 개나리와 벚꽃의 개화시기 변화를 조사하였는데, 그 결과 수종 및 지역 별로 개화시기 변화의 폭이 달리 나타났다. 개화시기가 상대적으로 늦은 벚꽃의 경우, 개나리보다 개화시기가 크게 단축되었으며 관측 지점 간의 개화일 변이도 크게 감소하였는데, 이 또한 최근 한반도에서 관측되는 늦봄의 급격한 기온 상승으로 인한 것으로 해석된다(Kim et al., 2015; Lee et al., 2014).
2. 모형 비교
전 지역에 대해 단일 모수를 추정하는 SM과 함께, SM에 지점별 보정계수를 도입한 MSM, 권역 내에서 단일 모수를 추정하는 GM, 관측 지점마다 개별적으로 모수를 추정하는 LM을 각각 개발하고 성능을 비교하였다. 훈련 결과, 전체 모형 중 LM이 가장 우수한 성능을 보였고, 검증 결과, 네 모형의 성능 차이가 거의 나타나지 않았던 남서부 지역을 제외하면 MSM과 LM이 다른 두 모형에 비해 양호한 성능을 보였다. 또한, Figure S3에 지역 평균 만개일의 표준편차와 모형의 성능을 비교한 결과를 연도별로 나타내었다. 지역 평균 만개일의 표준편차, 즉 만개일의 지역 편차[Figure S3(a)]는 2015년(1.58)에 가장 작았고, 2007년(6.97)과 2013년(6.97)에 가장 컸다. 2007~2017년의 기간 중 가장 최근 4년에 해당하는 2014, 2015, 2016, 2017년의 만개일 지역 편차는 나머지 7개 년도보다 작았다. 만개일의 지역 편차가 작았던 최근 4년 중 2017년을 제외한 3개 년도에서 LM의 성능이 가장 뛰어난 것으로 나타났다[Figure S3(b)]. 만개일의 지역 편차가 가장 컸던 2007, 2013년과 두번째로 컸던 2011년에는 MSM이 LM보다 더 좋은 성능을 보였다. 하지만 전체적으로 보았을 때, 특정 년도를 제외하면 LM과 MSM이 GM 및 SM에 비해 더 좋은 성능을 보였다. 특히, LM은 2012년과 2013년 두 해를 제외하면, GM과 SM보다 항상 더 좋은 성능을 보였다.
SM, MSM, GM, LM 중 비교적 좋은 성능을 보인 MSM과 LM을 선택하여 해당 모형의 예측 알고리즘을 전국 범위로 확대, 적용하였다. 알고리즘 적용 시, 위도 또는 고도가 높은 곳에 위치하여 다른 지역에 비해 아까시나무의 개화 시기가 상대적으로 느린 지역(5월 말~6월 개화 지역)까지 포괄해야 하므로, 봄철 평균기온으로써 3~5월 평균기온을 활용하였다.
MSM의 예측 알고리즘을 전국 범위로 확대하기 위하여, 모형을 구축한 26개 지점을 대상으로 분석 기간 중의 봄철 평균기온과 지점별 보정계수의 상관관계를 조사하였다. 그 결과, 두 변수는 양의 상관관계를 나타냈으며, 봄철 기온이 높은 지역일수록 보정계수가 증가하는 경향을 확인할 수 있었다[Figure 4(a)]. 이러한 상관관계를 바탕으로, 봄철 평균기온을 설명변수 x, 보정계수를 반응변수 y로 하는 선형회귀모형을 도출하였다. 모형의 적합도를 향상시키기 위해 R 패키지 car 을 활용하여 이상치 검정을 수행하였으며, 최종적으로 회귀직선의 방정식은 y=3.6034x‒40.8797로 추정되었다(결정계수 R2=0.7114)[Figure 4(a)].본 연구에서 모형의 입력자료로서 활용했던 과거 일기온 복원 래스터자료와 앞서 도출된 회귀식을 이용하여 MSM 보정계수의 전국 분포도를 1 km 해상도로 작성하였다. 작성된 보정계수 분포도를 활용하면 MSM을 전국적으로 적용하여, 아까시나무의 만개일을 l km 격자 단위로 예측할 수 있다.
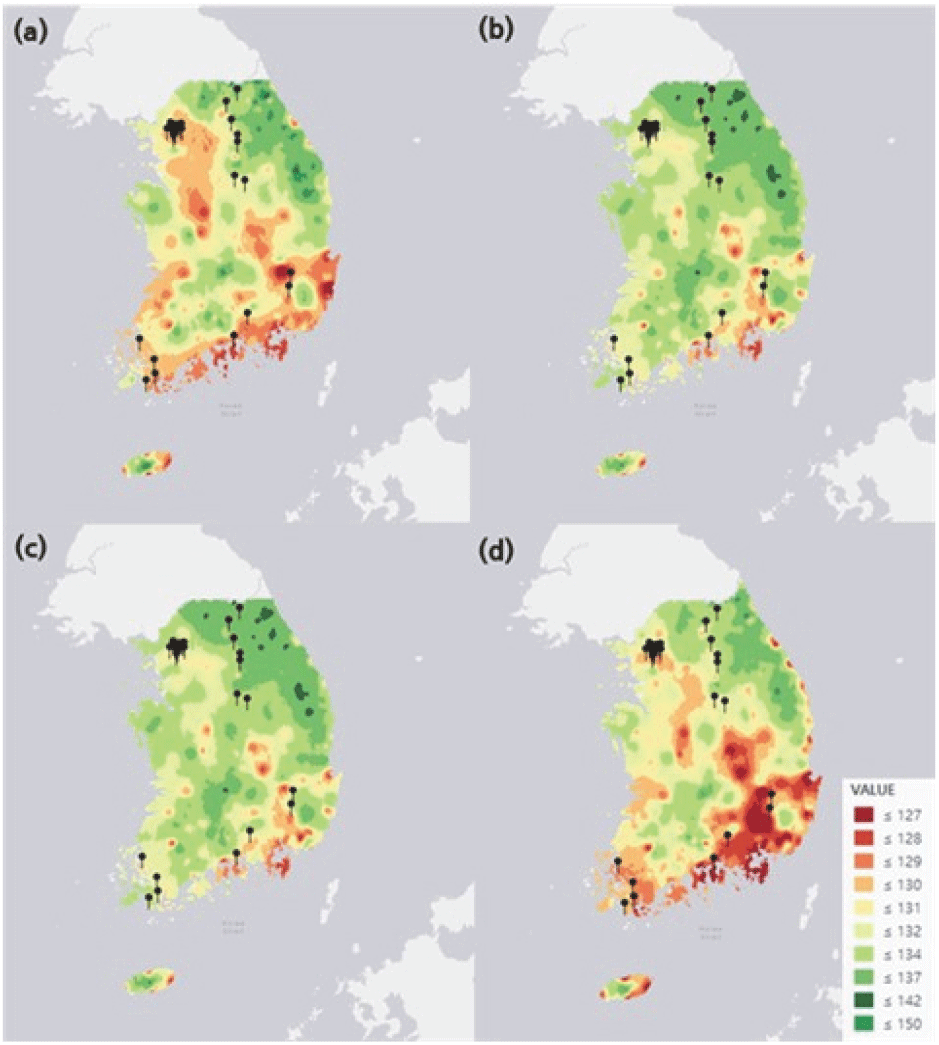
한편, 26개 지점에서 독립적으로 구축된 LM을 전국 범위의 예측에 적용하기 위하여 공간보간(spatial interpolation)을 통해 모형 개발 이외의 지역에서도 예측 만개일이 산출되도록 하였다. 이를 위해 26개 지점에서 각각 추정된 모수를 이용하여 지점별 만개일을 계산한 후, 코크리깅(co-kriging)을 수행하여 만개일의 전국 분포를 추정하였다(Figure 5). 만개 시기에 영향을 미치는 해당 년도의 봄철(3~5월) 평균기온을 코크리깅의 이차변수로 적용하였으며, 과거 일기온 복원 래스터 자료를 활용하여 1 km의 공간 해상도로 예측을 상세화 하였다.
Figure 5.
Spatial distribution of bloom dates of Robinia pseudoacacia in 4 years (2014~2017) estimated using co-kriging interpolation of Local Model (LM). (a) 2014, (b) 2015, (c) 2016, and (d) 2017.
Download Original Figure
MSM, LM의 예측 알고리즘을 전국 범위로 확대 적용 후, 최종적으로 모형이 개발된 이외 지역을 대상으로 모형의 예측력을 평가하기 위해 4년 간(2014~2017년) 16개의 추가 관측 지점에서 동일한 방법으로 관측된 만개일 자료를 활용하여, 외부 검증을 수행하였다. 그 결과, LM에 코크리깅 기법을 적용한 방법이 지점별로 보정계수를 추정하는 MSM보다 더 높은 정확도를 보였다(Table 5). 16개 지점 중 북강릉, 이천, 평택, 부안을 제외한 모든 곳에서, LM은 MSM보다 더 낮은 RMSE를 보였고 편의(Bias)는 0에 더 가까운 것으로 나타났다. 추가 관측 지점의 평균 RMSE는 LM이 MSM보다 1.78일 낮았으며(MSM:5.08, LM:3.30), 편의의 크기는 MSM이 LM에 비해 평균적으로 1.59일 더 컸다(MSM:-4.50, LM:-2.91). 또한 T 검정 결과, 두 모형의 RMSE, 편의의 분포는 통계적으로 유의한 차이를 보였다(RMSE: p-value=0.0118, Bias: p-value=0.0471). 즉, 개별 지역 모형은 수정 통합 모형보다 모형 개발 이외의 지역을 대상으로 더 나은 예측력을 보였다.
Table 5.
External validation results of the Modified Single Model (MSM) and Local Model (LM) using four years’ bloom dates observed at 16 additional sites, which were not included in model development. RMSE: Root mean square error.
| Site |
Model |
| MSM |
LM |
| RMSE |
Bias |
RMSE |
Bias |
| North Gangneung |
3.57 |
-3.25 |
4.06 |
-3.50 |
| Guri |
7.30 |
-7.25 |
7.04 |
-7.00 |
| Munmak |
6.61 |
-6.25 |
3.08 |
-3.00 |
| Yeoju |
6.65 |
-6.25 |
5.22 |
-4.75 |
| Yongin |
3.11 |
-2.33 |
2.38 |
-2.33 |
| Icheon |
3.16 |
-2.67 |
3.11 |
-3.00 |
| Pyeongtaek |
3.12 |
-1.75 |
3.81 |
-3.50 |
| Asan |
3.64 |
-3.25 |
2.55 |
-2.50 |
| Gongju |
6.76 |
-6.25 |
1.32 |
-0.75 |
| Nonsan |
4.61 |
-4.25 |
0.71 |
0.00 |
| Yeosan |
4.58 |
-4.00 |
2.12 |
-1.50 |
| Jeonju |
6.42 |
-6.25 |
5.27 |
-5.25 |
| Buan |
6.89 |
-6.50 |
7.52 |
-7.50 |
| Baekyangsa |
6.52 |
-6.50 |
2.29 |
-1.75 |
| Jangseong |
2.69 |
-0.75 |
1.22 |
-0.50 |
| Gwangju |
5.74 |
-4.50 |
1.12 |
0.25 |
Download Excel Table
결 론
본 연구를 통해 12년간(2006~2017년) 아까시나무 만개 시기의 지역별 변화 경향을 파악하고 동시에 이러한 변화 경향을 잘 설명할 수 있는 만개일 예측 모형을 개발하였다. 관측 기간 동안 남부 지역에 비해 봄철 기온 상승률이 높았던 중북부 내륙 지역의 만개일이 빠른 속도로 앞당겨졌고, 남부 지역과의 만개일 차이가 감소하였다. 만개일 예측에 있어 네 모형의 성능을 비교한 결과, 전국 또는 권역별로 동일한 모수를 추정하는 통합 모형보다, 지점별로 독립적인 모수를 추정하는 개별 모형이 더 좋은 성능을 보였다. 이는 기준온도, 저온요구량, 고온요구량과 같이 개화시기를 결정하는 수종 특이적 모수가 수목이 분포하고 있는 위도나 고도, 기타 환경조건에 따라 큰 변동성을 갖다는 점을 시사한다.
연구에 활용한 과정기반모형은 수목의 개화시기를 기온의 영향으로 설명하지만 수목의 개화시기는 광주기의 변화, 수분가용성 등 기타 환경조건에 의한 영향도 완전히 배제할 수 없다. 수종 및 지역에 따라 이러한 환경 인자별 중요도 또한 달리 나타날 수 있으므로 기온 이외의 환경 인자에 의한 영향도 추가적으로 고려할 필요가 있다. 본 연구는 보다 정확한 아까시나무의 개화시기 예측을 통해 이동형 양봉 농가의 채밀 활동을 효율적인 방향으로 개선하고 양봉 농가의 소득 안정화에 기여할 수 있을 것으로 기대된다.
감사의 글
본 연구는 산림청(국립산림과학원) ‘산악지역 영향예보 기반 구축 및 맞춤형 산악기상⋅기후 서비스 체계 개발’(과제번호: FE0500-2018-02)과 산림청(한국임업진흥원) 산림과학기술 연구개발사업‘(FTIS 2020185D10-2122-AA02)’의 지원에 의하여 이루어진 것입니다.
References
Aguilera, F. et al. 2015. Phenological models to predict the main flowering phases of olive (
Olea europaea L.) along a latitudinal and longitudinal gradient across the Mediterranean region. International Journal of Biometeorology 59(5): 629-641.

,


Basler, D. 2016. Evaluating phenological models for the prediction of leaf-out dates in six temperate tree species across central Europe. Agricultural and Forest Meteorology 217: 10-21.


Bertin, R.I. 2008. Plant phenology and distribution in relation to recent climate change. Journal of the Torrey Botanical Society 135(1): 126-146.


Blümel, K. and Chmielewski, F.M. 2012. Shortcomings of classical phenological forcing models and a way to overcome them. Agricultural and Forest Meteorology 164: 10-19.


Bogawski, P., Grewling, L. and Jackowiak, B. 2019. Predicting the onset of
Betula pendula flowering in Poznan (Poland) using remote sensing thermal data. Science of the Total Environment 658: 1485-1499.

,


Caffarra, A., Donnelly, A., Chuine, I. and Jones, M. 2011a. Modelling the timing of
Betula pubescens budburst. I. Temperature and photoperiod: a conceptual model. Climate Research 46(2): 147-157.


Caffarra, A., Donnelly, A. and Chuine, I. 2011b. Modelling the timing of
Betula pubescens budburst. II. Integrating complex effects of photoperiod into process-based models. Climate Research 46: 159-170.


Campbell, R.K. and Sorensen, F.C. 1973. Cold‐acclimation in seedling Douglas‐fir related to phenology and provenance. Ecology 54(5): 1148-1151.


Campoy, J.A., Ruiz, D., Allderman, L., Cook, N. and Egea, J. 2012. The fulfilment of chilling requirements and the adaptation of apricot (
Prunus armeniaca L.) in warm winter climates: An approach in Murcia (Spain) and the Western Cape (South Africa). European Journal of Agronomy 37(1): 43-55.


Cesaraccio, C., Spano, D., Snyder, R.L. and Duce, P. 2004. Chilling and forcing model to predict bud-burst of crop and forest species. Agricultural and Forest Meteorology, 126(1): 1-13.


Cesaraccio, C., Spano, D., Snyder, R.L. and Duce, P. 2005. Corrigendum to ‘‘Chilling and forcing model to predict bud-burst of crop and forest species’’. Agricultural and Forest Meteorology 129(3): 211.


Chmielewski, F.-M. and Götz, K.-P. 2016. Performance of models for the beginning of sweet cherry blossom under current and changed climate conditions. Agricultural and Forest Meteorology 218-219: 85-91.


Chuine, I., Cour, P., Rousseau, D.D. 1998. Fitting models predicting dates of flowering of temperate‐zone trees using simulated annealing. Cell and Environment, 21(5): 455-466.


Chun, J. 2016. Modelling of Peach Tree (
Prunus persica) Full Blooming Dates Using APCC MME Seasonal Forecasts, APEC Climate Center, Busan.

Chung, U., Jung, J., Seo, H. and Yun, J.I. 2009. Using urban effect corrected temperature data and a tree phenology model to project geographical shift of cherry flowering date in South Korea. Climatic Change 93(3): 447-463.


Duputié, A., Rutschmann, A., Ronce, O. and Chuine. 2015. Phenological plasticity will not help all species adapt to climate change. Global Change Biology 21(8): 3062-3073.

,


Gehan, E. A. 1965. A generalized Wilcoxon test for comparing arbitrarily singly-censored samples. Biometrika 52(1-2): 203-224.

,


Ge, Q., Wang, H., Rutishauser, T. and Dai, J. 2015. Phenological response to climate change in China: a meta-analysis. Global Change Biology 21(1): 265-274.

,


Gonsamo, A., Chen, J.M. and Wu, C. 2013. Citizen Science: linking the recent rapid advances of plant flowering in Canada with climate variability. Scientific Reports 3(1): 2239.

,

,


Hänninen, H. 1990. Modelling bud dormancy release in trees from cool and temperate regions. Acta Forestalia Fennica 213: 1-47.


Harrington, C.A., Gould, P.J., Clair, B. 2010. Modeling the effects of winter environment on dormancy release of Douglas-fir. Forest Ecology and Management 259(4): 798-808.


Horvath, D.P., Anderson, J.V., Chao, W.S. and Foley, M.E. 2003. Knowing when to grow: signals regulating bud dormancy. Trends in Plant Science 8(11): 534-540.

,


Jung, C. and Chon, J.-W. 2016. Quality assessment of honey from different floral origin in Korea. Korean Journal of Apiculture 31(2): 103-111.


Jung, C. and Lee, M.-l. 2018. Beekeeping in Korea: Past, Present, and Future Challenges. pp. 175-197. In: Chantawannakul, P., Williams G.C., Neumann, P. and Williams, G.R. (Ed.). Asian Beekeeping in the 21st Century. Springer. Singapore.

,


Jung, J.E, Kwon, E.Y., Chung, U. and Yun, J.I. 2005. Predicting Cherry Flowering Date Using a Plant Phonology Model. Korean Journal of Agricultural and Forest Meteorology 7(2): 148-155.

Kalvans, A., Bitane, M. and Kalvane, G. 2015. Forecasting plant phenology: evaluating the phenological models for Betula pendula and Padus racemosa spring phases, Latvia. International Journal of Biometeorology 59(2): 165-179.

,


Kim, J.-H., Cheon, J.-H. and Yun, J.I. 2013a. Outlook on blooming dates of spring flowers in the Korean Peninsula under the RCP 8.5 projected climate. Korean Journal of Agricultural and Forest Meteorology 15(1): 50-58.


Kim, J.-H., Lee, E.-J. and Yun, J.I. 2013b. Prediction of blooming dates of spring flowers by using digital temperature forecasts and phenology models. Korean Journal of Agricultural and Forest Meteorology 15(1): 40-49.


Kim, J.-H., Yun, E.-j., Kim, D.-j., Kang, D., Seo, B.H. and Shim, K.M. 2020. Evaluation of Regional Flowering Phenological Models in Niitaka Pear by Temperature Patterns. Korean Journal of Agricultural and Forest Meteorology 22(4): 268-278.

Kim, J.-H., Kim, S.-O., Kim, D.-J., Moon, K.H. and Yun, J.I. 2015. Using daily temperature to predict phenology trends in spring flowers. Asia-Pacific Journal of Atmospheric Sciences 51(2): 167-172.

,


Kohsaka, R., Park, M.S. and Uchiyama, Y. 2017. Beekeeping and honey production in Japan and South Korea: past and present. Journal of Ethnic Foods 4(2): 72-79.


Kwon, J.-H., Nam, E.-Y., Yun, S.-K., Kim, S.-J., Song, S.-Y., Lee, J.-H. and Hwang, K.-d. 2020. Chilling and heat requirement of peach cultivars and changes in chilling accumulation spectrums based on 100-year records in Republic of Korea Agricultural and Forest Meteorology 288-289: 108009.


Lang, G., Early, J., Martin, G. and Darnell, R.L. 1987. Endo-, para-, and ecodormancy: physiological terminology and classification for dormancy research. HortScience 22(3): 371-377.

Lee, H.-S., Kim, J.-H., and Yun, J.I. 2014. Recent trends in blooming dates of spring flowers and the observed disturbance in 2014. Korean Journal of Agricultural and Forest Meteorology 16(4): 396-402.


Lee, K.-M., Kwon, W.-T. and Lee, S.-H. 2009. A study on plant phenological trends in South Korea. Journal of the Korean Association of Regional Geographers 15(3): 337-350.

Linkosalo, T., Lappalainen, H.K. and Hari, P. 2008. A comparison of phenological models of leaf bud burst and flowering of boreal trees using independent observations. Tree Physiology 28(12): 1873-1882.

,


Liu, G.H., Chen, X.Q., Fu, Y.S. and Delpierre, N. 2019. Modelling leaf coloration dates over temperate China by considering effects of leafy season climate. Ecological Modelling 394: 34-43.


Liu, Q., Fu, Y.H., Liu, Y., Janssens, I.A. and Piao, S. 2018. Simulating the onset of spring vegetation growth across the Northern Hemisphere. Global Change Biology 24(3): 1342-1356.

,


Ma, Q., Huang, J.-G., Hänninen, H. and Berninger, F.J. 2018. Reduced geographical variability in spring phenology of temperate trees with recent warming. Agricultural and Forest Meteorology 256: 526-533.


Matzneller, P., Blümel, K. and Chmielewski, F.-M. 2014. Models for the beginning of sour cherry blossom. International Journal of Biometeorology 58(5): 703-715.

,


Menzel, A. et al., 2006. European phenological response to climate change matches the warming pattern. Global Change Biology 12(10): 1969-1976.


NiFoS (National Institute of Forest Science). 2016. Reduced regional variation in flowering time of
Robinia pseudoacacia, and the urgent need to find alternative honey plants.
https://nifos.forest.go.kr (2017. 05. 31).

NiFoS (National Institute of Forest Science). 2017. The flowering period of
Robinia pseudoacacia plummeted by 50% compared to 10 years ago.
https://nifos.forest.go.kr (2017. 05. 31).

Pereira, M.R., Ribeiro, H., Abreu, I., Eiras-Dias, J., Mota, T. and Cunha, Mário. 2018. Predicting the flowering date of Portuguese grapevine varieties using temperature-based phenological models: a multi-site approach. The Journal of Agricultural Science 156(7): 865-876.


Rea, R. and Eccel, E. 2006. Phenological models for blooming of apple in a mountainous region. International Journal of Biometeorology 51(1): 1-16.

,


Roberts, A.M.I., Tansey, C., Smithers, R.J. and Phillimore, A.B. 2015. Predicting a change in the order of spring phenology in temperate forests. Global Change Biology 21(7): 2603-2611.

,

,


Ruml, M., Korać, N., Vujadinović, M., Vuković, A. and Ivanišević, D. 2016. Response of grapevine phenology to recent temperature change and variability in the wine-producing area of Sremski Karlovci, Serbia. The Journal of Agricultural Science 154(2): 186-206.


Shi, P., Chen, Z., Reddy, G.V.P., Hui, C., Huang, J. and Xiao, M. 2017. Timing of cherry tree blooming: Contrasting effects of rising winter low temperatures and early spring temperatures. Agricultural and Forest Meteorology 240: 78-89.


Tanino, K.K., Kalcsits, L., Silim, S., Kendall, E. and Gray, G. 2010. Temperature-driven plasticity in growth cessation and dormancy development in deciduous woody plants: a working hypothesis suggesting how molecular and cellular function is affected by temperature during dormancy induction. Plant Molecular Biology 73(1): 49-65.

,


Templ, B. et al., 2017. Phenological patterns of flowering across biogeographical regions of Europe. International Journal of Biometeorology 61(7): 1347-1358.

,


Vitasse, Y., Hoch, G., Randin, C.F., Lenz, A., Kollas, C., Scheepens, J. F. and Körner, C. 2013. Elevational adaptation and plasticity in seedling phenology of temperate deciduous tree species. Oecologia 171(3): 663-678.

,


Vitasse, Y., Signarbieux, C. and Fu, Y. H. 2018. Global warming leads to more uniform spring phenology across elevations. Proceedings of the National Academy of Sciences 115(5): 1004-1008.

,

,


Xiang, Y., Gubian, S., Suomela, B. and Hoeng, J. 2013. Generalized Simulated Annealing for Global Optimization: the GenSA Package. R Journal 5(1).


Yu, J. et al., 2020. Distinctive Gene Expression Patterns Define Endodormancy to Ecodormancy Transition in Apricot and Peach. Frontiers in Plant Science 11: 180.


Yun, J.I. 2006. Climate change impact on the flowering season of Japanese cherry
(Prunus serrulata var.
spontanea) in Korea during 1941-2100. Korean Journal of Agricultural and Forest Meteorology 8(2): 68-76.

Yun, J. I., Choi, J.-Y. and Ahn, J.-H. (2001). Seasonal Trend of Elevation Effect on Daily Air Temperature in Korea. Korean Journal of Agricultural and Forest Meteorology 3(2): 96-104

Yun, K., Hsiao, J., Jung, M.-P., Choi, I.-T., Glenn, D.M., Shim, K.-M. and Kim, S.-H. 2017. Can a multi-model ensemble improve phenology predictions for climate change studies?. Ecological Modelling 362: 54-64.


Supplementary Material
Table S1.
Optimal parameters estimated using calibration dataset in MSM, GM, and LM. MSM: Modifid Single Model, GM: Group Model, LM: Local Model, MUP: Mt. Ujang Park, GE: Gangbyeon Expressway, SNC: Seoul National Cemetery, SCGP: Seoul Children’s Grand Park, TB: base temperature, C*: chilling requirement, F*: forcing requirement, °D: degree days.
| Site |
MSM |
GM |
LM |
| TB [°C] |
C* [°D] |
F* [°D] |
Correction factor |
TB [°C] |
C* [°D] |
F* [°D] |
TB [°C] |
C* [°D] |
F* [°D] |
| Mokpo |
8.86 |
-138.95 |
247.73 |
4.4286 |
3.92 |
-123.49 |
554.44 |
14.22 |
-42.24 |
94.10 |
| Haenam |
8.86 |
-138.95 |
247.73 |
2.1429 |
3.92 |
-123.49 |
554.44 |
3.79 |
-80.16 |
588.64 |
| Ttangkkeut |
8.86 |
-138.95 |
247.73 |
4.8571 |
3.92 |
-123.49 |
554.44 |
4.94 |
-181.70 |
481.13 |
| Wando |
8.86 |
-138.95 |
247.73 |
1.8571 |
3.92 |
-123.49 |
554.44 |
5.21 |
-178.54 |
446.94 |
| Namhae |
8.86 |
-138.95 |
247.73 |
7.1429 |
10.60 |
-172.01 |
205.76 |
4.36 |
-132.62 |
599.57 |
| Jinju |
8.86 |
-138.95 |
247.73 |
5.0000 |
10.60 |
-172.01 |
205.76 |
3.97 |
-159.98 |
567.58 |
| Miryang |
8.86 |
-138.95 |
247.73 |
5.5714 |
10.60 |
-172.01 |
205.76 |
3.23 |
-149.05 |
576.53 |
| Cheongdo |
8.86 |
-138.95 |
247.73 |
1.2857 |
10.60 |
-172.01 |
205.76 |
14.18 |
-75.43 |
83.28 |
| Chungju |
8.86 |
-138.95 |
247.73 |
-5.3333 |
6.28 |
-67.99 |
363.91 |
12.11 |
-105.04 |
112.63 |
| Jecheon |
8.86 |
-138.95 |
247.73 |
-5.5000 |
6.28 |
-67.99 |
363.91 |
3.33 |
-96.90 |
478.46 |
| Yanggu |
8.86 |
-138.95 |
247.73 |
1.6667 |
6.28 |
-67.99 |
363.91 |
14.59 |
-43.06 |
100.08 |
| Chuncheon |
8.86 |
-138.95 |
247.73 |
-3.3333 |
6.28 |
-67.99 |
363.91 |
3.77 |
-57.31 |
494.26 |
| Hongcheon |
8.86 |
-138.95 |
247.73 |
6.1667 |
6.28 |
-67.99 |
363.91 |
2.63 |
-109.88 |
598.12 |
| Hoengseong |
8.86 |
-138.95 |
247.73 |
-7.5000 |
6.28 |
-67.99 |
363.91 |
4.25 |
-166.55 |
340.00 |
| Wonju |
8.86 |
-138.95 |
247.73 |
1.3333 |
6.28 |
-67.99 |
363.91 |
13.72 |
-99.29 |
101.94 |
| Mt. Gwanak |
8.86 |
-138.95 |
247.73 |
-11.1429 |
3.28 |
-52.45 |
527.81 |
5.35 |
-117.27 |
280.60 |
| SNC |
8.86 |
-138.95 |
247.73 |
-6.5714 |
3.28 |
-52.45 |
527.81 |
6.71 |
-54.75 |
298.41 |
| Mt. Nam |
8.86 |
-138.95 |
247.73 |
1.4286 |
3.28 |
-52.45 |
527.81 |
8.16 |
-189.40 |
280.36 |
| GE |
8.86 |
-138.95 |
247.73 |
-3.0000 |
3.28 |
-52.45 |
527.81 |
12.87 |
-52.65 |
112.24 |
| MUP |
8.86 |
-138.95 |
247.73 |
-1.0000 |
3.28 |
-52.45 |
527.81 |
2.60 |
-62.26 |
563.74 |
| Seooreung |
8.86 |
-138.95 |
247.73 |
6.1429 |
3.28 |
-52.45 |
527.81 |
3.73 |
-102.57 |
568.75 |
| Jeongneung |
8.86 |
-138.95 |
247.73 |
-1.8571 |
3.28 |
-52.45 |
527.81 |
6.89 |
-52.99 |
328.71 |
| Mt. Bukak |
8.86 |
-138.95 |
247.73 |
2.4286 |
3.28 |
-52.45 |
527.81 |
7.76 |
-45.99 |
318.34 |
| Hongneung |
8.86 |
-138.95 |
247.73 |
0.1667 |
3.28 |
-52.45 |
527.81 |
14.80 |
-67.51 |
72.09 |
| SCGP |
8.86 |
-138.95 |
247.73 |
-3.1429 |
3.28 |
-52.45 |
527.81 |
13.73 |
-40.13 |
91.41 |
| Taereung |
8.86 |
-138.95 |
247.73 |
-3.5000 |
3.28 |
-52.45 |
527.81 |
15.00 |
-59.21 |
63.56 |
Download Excel Table
Table S2.
Model performance in (a) calibration dataset (b) validation dataset. RMSE, Bias, and Pearson’s correlation coefficient were used as an evaluation index of performance. MUP: Mt. Ujang Park, GE: Gangbyeon Expressway, SNC: Seoul National Cemetery, SCGP: Seoul Children’s Grand Park, RMSE: Root Mean Square Error, r: Pearson’s correlation coefficient.
| (a) |
| Site |
SM |
MSM |
GM |
LM |
| RMSE |
Bias |
r |
RMSE |
Bias |
r |
RMSE |
Bias |
r |
RMSE |
Bias |
r |
| Mokpo |
6.04 |
-4.43 |
0.50 |
4.10 |
-4.39×10-13 |
0.50 |
3.09 |
-0.71 |
0.65 |
2.39 |
0.00 |
0.64 |
| Haenam |
4.23 |
-2.14 |
0.64 |
3.64 |
-1.46×10-13 |
0.64 |
2.98 |
0.00 |
0.57 |
2.48 |
-0.43 |
0.65 |
| Ttangkkeut |
5.29 |
-4.86 |
0.82 |
2.10 |
1.46×10-13 |
0.82 |
2.33 |
-1.71 |
0.92 |
1.60 |
-0.29 |
0.96 |
| Wando |
3.61 |
-1.86 |
0.77 |
3.09 |
1.46×10-13 |
0.77 |
2.70 |
0.71 |
0.81 |
1.96 |
0.14 |
0.91 |
| Namhae |
7.82 |
-7.14 |
0.67 |
3.18 |
-1.46×10-13 |
0.67 |
4.05 |
-2.14 |
0.69 |
2.14 |
0.57 |
0.83 |
| Jinju |
5.84 |
-5.00 |
0.89 |
3.02 |
0 |
0.89 |
2.93 |
-0.57 |
0.90 |
1.65 |
0.14 |
0.93 |
| Miryang |
6.96 |
-5.57 |
0.72 |
4.17 |
4.32×10-13 |
0.72 |
4.09 |
-0.71 |
0.70 |
2.83 |
0.00 |
0.82 |
| Cheongdo |
2.80 |
-1.29 |
0.88 |
2.49 |
-2.92×10-13 |
0.88 |
4.33 |
3.29 |
0.80 |
2.14 |
-0.29 |
0.89 |
| Chungju |
6.45 |
5.33 |
0.64 |
3.64 |
3.32×10-13 |
0.64 |
5.18 |
3.50 |
0.66 |
2.55 |
-1.17 |
0.74 |
| Jecheon |
5.85 |
5.50 |
0.95 |
1.98 |
0 |
0.95 |
4.08 |
3.33 |
0.92 |
1.68 |
-0.50 |
0.97 |
| Yanggu |
5.97 |
-1.67 |
0.75 |
5.73 |
3.32×10-13 |
0.75 |
6.24 |
-2.67 |
0.76 |
4.08 |
-0.33 |
0.91 |
| Chuncheon |
3.92 |
3.33 |
0.94 |
2.05 |
3.32×10-13 |
0.94 |
2.77 |
2.00 |
0.96 |
1.83 |
0.33 |
0.95 |
| Hongcheon |
6.99 |
-6.17 |
0.74 |
3.29 |
3.32×10-13 |
0.74 |
7.35 |
-6.67 |
0.78 |
2.74 |
-0.50 |
0.90 |
| Hoengseong |
8.63 |
7.50 |
0.81 |
4.27 |
0 |
0.81 |
7.62 |
6.33 |
0.84 |
4.12 |
0.33 |
0.85 |
| Wonju |
4.43 |
-1.33 |
0.82 |
4.23 |
-3.32×10-13 |
0.82 |
4.95 |
-2.50 |
0.86 |
3.39 |
-1.17 |
0.63 |
| Mt. Gwanak |
12.47 |
11.14 |
0.72 |
5.59 |
1.46×10-13 |
0.72 |
10.27 |
8.57 |
0.78 |
5.81 |
-1.14 |
0.81 |
| SNC |
8.05 |
6.57 |
0.80 |
4.66 |
-4.36×10-13 |
0.80 |
6.32 |
4.29 |
0.84 |
4.04 |
0.00 |
0.90 |
| Mt. Nam |
2.93 |
-1.43 |
0.95 |
2.56 |
-4.39×10-13 |
0.95 |
3.89 |
-2.86 |
0.95 |
1.81 |
0.43 |
0.98 |
| GE |
4.73 |
3.00 |
0.88 |
3.65 |
0 |
0.88 |
3.63 |
1.17 |
0.88 |
1.91 |
0.00 |
0.94 |
| MUP |
6.34 |
1.00 |
0.69 |
6.26 |
0 |
0.69 |
6.12 |
-1.43 |
0.74 |
5.33 |
-0.43 |
0.77 |
| Seooreung |
8.06 |
-6.14 |
0.77 |
5.22 |
-1.46×10-13 |
0.77 |
9.28 |
-7.86 |
0.78 |
4.49 |
0.43 |
0.81 |
| Jeongneung |
2.75 |
1.86 |
0.95 |
2.03 |
-1.46×10-13 |
0.95 |
2.24 |
-0.43 |
0.96 |
1.69 |
0.00 |
0.97 |
| Mt. Bukak |
4.02 |
-2.43 |
0.86 |
3.20 |
-4.39×10-13 |
0.86 |
5.90 |
-4.86 |
0.84 |
3.05 |
-0.71 |
0.90 |
| Hongneung |
3.98 |
-0.17 |
0.90 |
3.98 |
3.32×10-13 |
0.90 |
4.47 |
-2.33 |
0.91 |
2.61 |
-0.50 |
0.92 |
| SCGP |
6.02 |
3.14 |
0.78 |
5.14 |
1.46×10-13 |
0.78 |
5.52 |
1.57 |
0.79 |
3.78 |
-0.86 |
0.81 |
| Taereung |
4.67 |
3.50 |
0.95 |
3.10 |
0 |
0.95 |
3.37 |
1.67 |
0.96 |
1.73 |
0.67 |
0.95 |
| (b) |
| Site |
SM |
MSM |
GM |
LM |
| RMSE |
Bias |
r |
RMSE |
Bias |
r |
RMSE |
Bias |
r |
RMSE |
Bias |
r |
| Mokpo |
3.90 |
0.00 |
0.6667 |
5.90 |
4.43 |
0.67 |
5.73 |
2.80 |
0.58 |
6.15 |
3.00 |
0.63 |
| Haenam |
1.73 |
-0.20 |
0.956 |
2.60 |
1.94 |
0.96 |
2.86 |
1.00 |
0.80 |
2.72 |
1.40 |
0.83 |
| Ttangkkeut |
5.46 |
-3.00 |
0.3331 |
4.92 |
1.86 |
0.33 |
5.25 |
-1.20 |
0.44 |
5.48 |
1.20 |
0.30 |
| Wando |
4.22 |
-0.60 |
0.5366 |
4.36 |
1.26 |
0.54 |
4.20 |
1.20 |
0.66 |
3.95 |
1.20 |
0.68 |
| Namhae |
8.33 |
-5.80 |
-0.0025 |
6.13 |
1.34 |
0.00 |
6.26 |
-2.00 |
0.00 |
5.48 |
0.80 |
0.12 |
| Jinju |
5.80 |
-1.60 |
0.3764 |
6.53 |
3.40 |
0.38 |
5.98 |
3.40 |
0.46 |
6.23 |
3.60 |
0.48 |
| Miryang |
7.67 |
-3.20 |
-0.1894 |
7.36 |
2.37 |
-0.19 |
6.59 |
0.60 |
-0.03 |
6.66 |
1.60 |
-0.10 |
| Cheongdo |
3.66 |
0.20 |
0.3517 |
3.95 |
1.49 |
0.35 |
5.74 |
4.20 |
0.22 |
2.65 |
-0.60 |
0.71 |
| Chungju |
7.22 |
7.00 |
0.8756 |
2.44 |
1.67 |
0.88 |
5.55 |
5.20 |
0.86 |
4.56 |
1.20 |
0.86 |
| Jecheon |
5.48 |
5.20 |
0.9913 |
1.75 |
-0.30 |
0.99 |
3.71 |
3.00 |
0.97 |
3.58 |
-0.40 |
0.80 |
| Yanggu |
5.20 |
-4.60 |
0.9486 |
3.80 |
-2.93 |
0.95 |
5.69 |
-5.20 |
0.96 |
4.27 |
-2.20 |
0.83 |
| Chuncheon |
3.13 |
3.00 |
0.9868 |
0.95 |
-0.33 |
0.99 |
2.72 |
2.20 |
0.96 |
2.14 |
0.60 |
0.93 |
| Hongcheon |
4.90 |
-2.40 |
0.7222 |
5.69 |
3.77 |
0.72 |
6.03 |
-3.60 |
0.62 |
6.63 |
2.00 |
0.39 |
| Hoengseong |
5.69 |
4.80 |
0.9091 |
4.08 |
-2.70 |
0.91 |
4.63 |
3.40 |
0.90 |
4.38 |
-3.60 |
0.94 |
| Wonju |
2.49 |
1.40 |
0.9288 |
3.42 |
2.73 |
0.93 |
1.95 |
-0.20 |
0.92 |
4.02 |
1.00 |
0.90 |
| Mt. Gwanak |
13.29 |
12.60 |
0.8815 |
4.47 |
1.46 |
0.88 |
10.03 |
9.40 |
0.85 |
4.98 |
-0.40 |
0.78 |
| SNC |
7.28 |
7.00 |
0.9584 |
2.05 |
0.43 |
0.96 |
5.57 |
5.00 |
0.93 |
3.16 |
2.00 |
0.95 |
| Mt. Nam |
3.63 |
1.60 |
0.8029 |
4.45 |
3.03 |
0.80 |
4.10 |
-0.80 |
0.66 |
4.34 |
2.40 |
0.75 |
| GE |
4.60 |
4.40 |
0.9932 |
1.95 |
1.40 |
0.99 |
3.16 |
1.60 |
0.89 |
5.67 |
3.00 |
0.92 |
| MUP |
5.06 |
4.00 |
0.885 |
4.31 |
3.00 |
0.89 |
3.95 |
1.20 |
0.80 |
4.77 |
1.60 |
0.75 |
| Seooreung |
4.15 |
-2.40 |
0.8399 |
5.04 |
3.74 |
0.84 |
7.16 |
-5.20 |
0.65 |
5.60 |
1.80 |
0.58 |
| Jeongneung |
6.48 |
6.00 |
0.8982 |
4.81 |
4.14 |
0.90 |
5.16 |
3.40 |
0.78 |
5.35 |
4.60 |
0.87 |
| Mt. Bukak |
3.29 |
-2.00 |
0.9273 |
2.64 |
0.43 |
0.93 |
6.71 |
-5.00 |
0.73 |
3.44 |
-0.60 |
0.85 |
| Hongneung |
6.42 |
4.00 |
0.7598 |
6.52 |
4.17 |
0.76 |
5.57 |
1.00 |
0.75 |
6.66 |
3.60 |
0.75 |
| SCGP |
7.39 |
6.60 |
0.9073 |
4.79 |
3.46 |
0.91 |
5.42 |
3.80 |
0.87 |
7.21 |
4.40 |
0.87 |
| Taereung |
9.57 |
8.00 |
0.7208 |
6.92 |
4.50 |
0.72 |
8.10 |
5.20 |
0.64 |
8.45 |
6.20 |
0.75 |
Download Excel Table
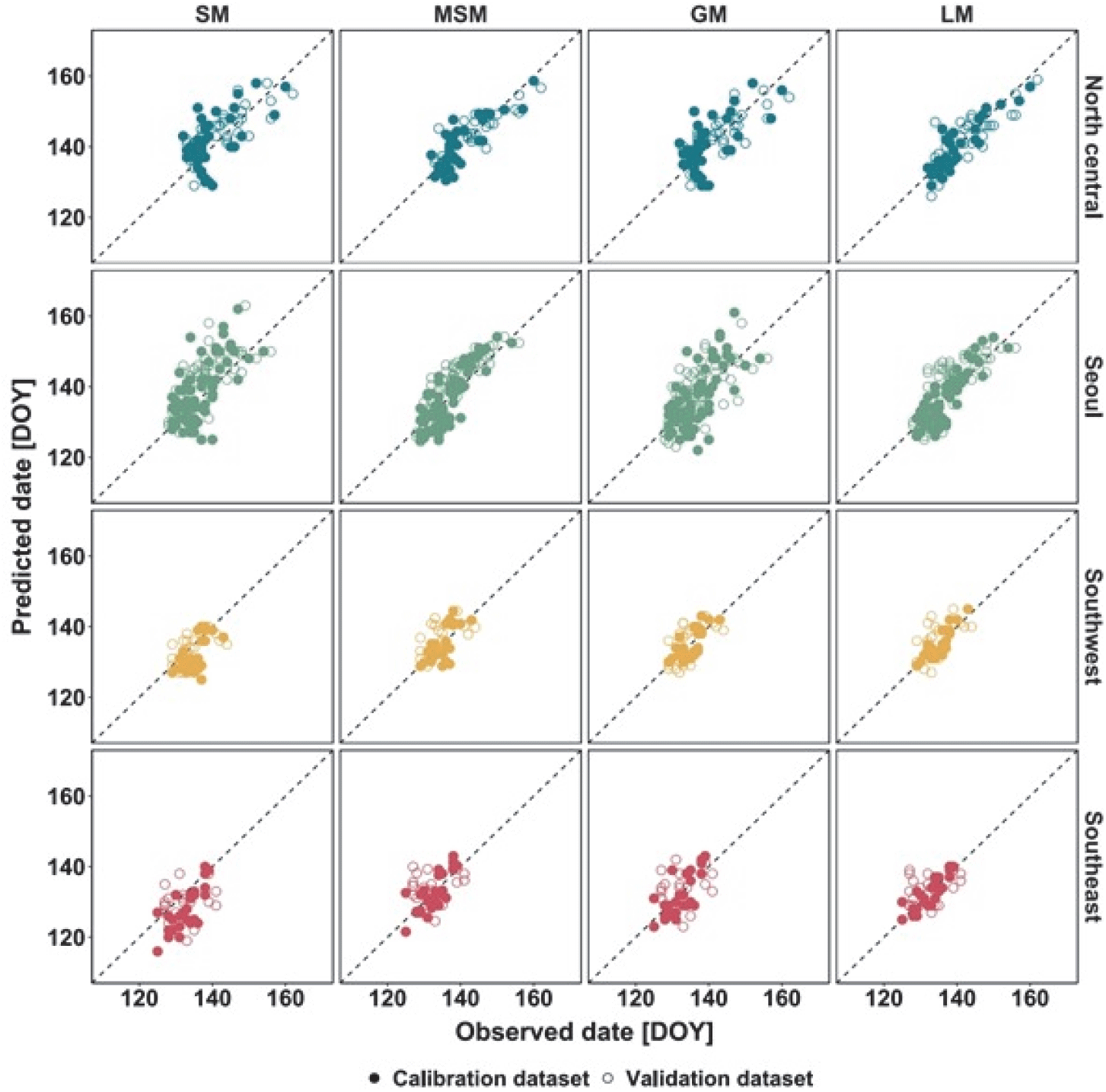
Figure S1.
Scatter plots of observed vs. predicted blooming dates for calibration (closed circle) and validation dataset (open circle) using Single Model (SM), Modified Single Model (MSM), Group Model (GM) and Local Model (LM).
Download Original Figure
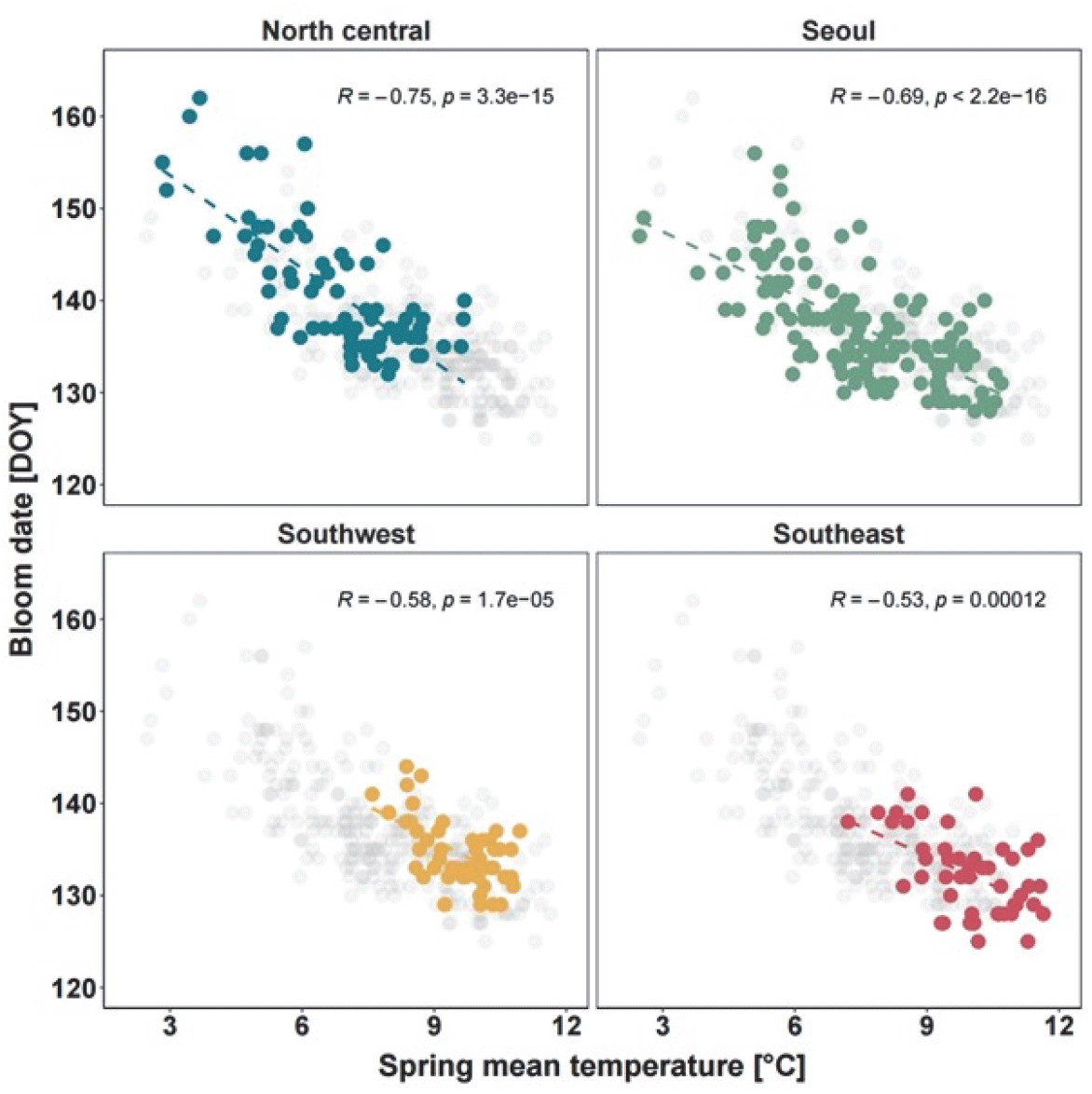
Figure S2.
Correlation between spring (March, April) temperature and the bloom date of Robinia pseudoacacia in North central, Seoul, Southwest, and Southeast regions.
Download Original Figure
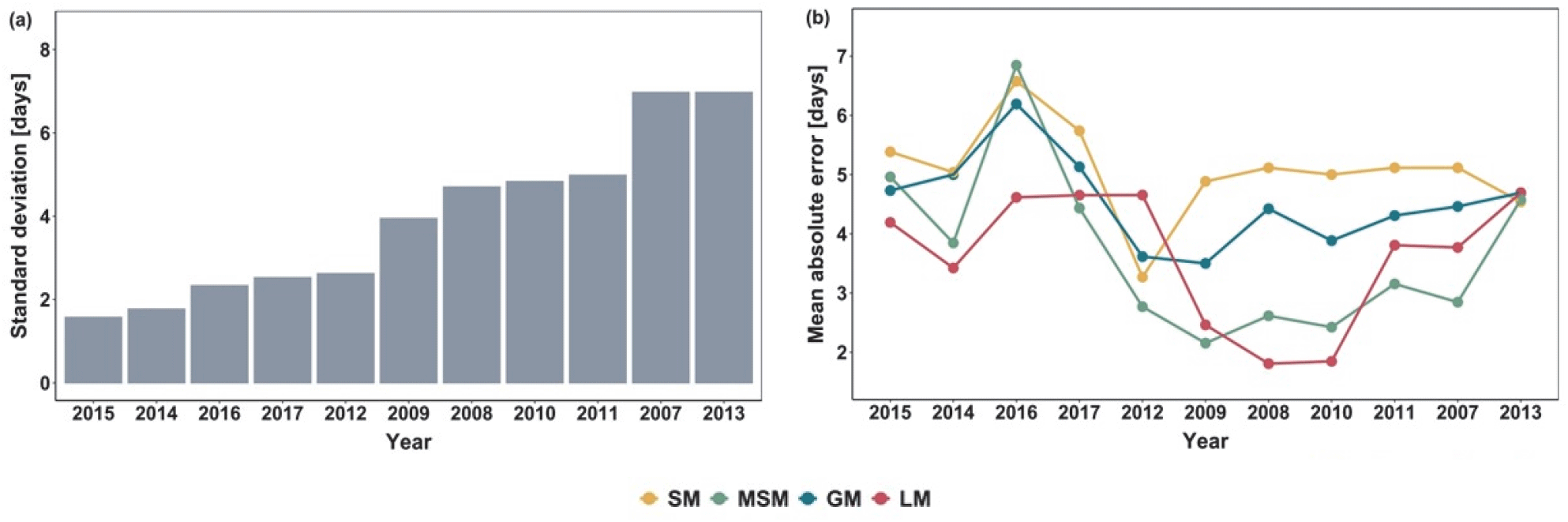
Figure S3.
(a) Variation of bloom dates for Robinia pseudoacacia in four regions and (b) Mean absolute error of four different models by year. SM: Single Model, MSM: Modified Single Model, GM: Group Model, LM: Local Model.
Download Original Figure