서 론
산림에서 생장은 시간의 경과에 따라 일정 임분상에서 하나 또는 다수의 개체목 크기의 증가를 일컫는다. 생장과 수확은 수학적으로 서로 연관이 있어, 수확은 연간생장량의 누적이라 표현할 수 있으며, 또한 생장은 수확을 나타내는 함수 상에서의 그 변화율이라 말할 수 있다.
산림에서의 생장에 따른 수확량 및 시장으로의 판매계획을 위해 생장예측이 필요하며, 또한 생장과 비례하는 벌채를 결정하기 위하여 생장의 예측이 필요하다. 토지이용자 측면에서는 특정한 입지의 합리적인 경영결정을 위해 생장예측이 필요하다. 그리고 다른 경영체제 및 조림적 시업하에서의 선택과 비교, 즉 가장 최적의 생육공간, 간벌의 주기 및 강도 등을 결정하는데도 수확량에 대한 생장예측(모델)은 필수적이다.
산림생장모델이 문헌상으로 밝혀진 시작은 1700년대 유럽에서의 생장 및 수확량을 구명하기 위해 시험지를 구축한데서 시작한다고 볼 수 있으며, 이후 1910년 후반에 이르러 지위(site quality)의 개념을 정의하는데 수고생장이 제시된 바 있었다(Reineke, 1927; Hamilton, 1988). 산림생장모델에 대한 본격적인 연구는 1930년에 들면서 부터이다. 지위지수 곡선의 도출과 Bertalanffy 및 Schumacher 생장식이 개발되었으며, 임분밀도에 대한 연구가 활발히 이뤄졌다. 1960년대는 다양한 임목생장 및 수확식이 개발되었고 개체목 거리종속모델 및 임목생장을 선형이 아닌 비선형이 가능함을 제시하기도 하였으며, 요즘까지도 방법론으로 활용되는 수간곡선을 이용하는 재적식이 개발되었다. 1970년대는 임분구조 변화를 구명할 수 있는 직경분포모델을 Weibull 분포를 적용하였으며, 이후 다양한 전산처리방법 및 모듈이 개발되면서 몇 개의 모델을 연결하며 전체 산림의 조성에서 생장, 고사, 수확까지를 해석할 수 있는 혼합모델이 개발되었다(Avery, 1967; Vanclay, 1994; Weiskittel et al., 2011).
산림생장을 연구하는 분야에서는 일반성을 갖는 생장 및 생장법칙 구명을 위한 연구가 명제이며 현재도 지속적으로 연구되고 있다. 그러나 산림에서의 생물적인 진행과정은 대단히 복잡하고 계속적으로 변화하기 때문에 이를 완전하게 파악한다는 것은 불가능하다. 그 중 구명된 사실중의 하나는 시간의 경과에 따른 임목의 생장(특히, 수고생장)이 S자 곡선을 이룬다는 것이다(Clutter et al., 1983). 이를 설명하기 위하여 Backman(1942)은 수고생장은 수령이 증가할수록 생장에 대한 물리적 시간의 영향력은 뚜렷이 감소한다고 한 바 있다(Byun et al., 1996). 생장법칙을 설명함에 있어 Bertalanffy(1951)의 연구는 커다란 의의를 갖는데, 이 연구는 동물의 생장과정을 설명하기 위하여 상대생장 함수(allometric function)를 이용하였다는 점이다. 임학에서는 Thomasius(1963)에 의해, 개체목 및 임분생장을 구명하는 연구에서 이 함수식이 응용되면서 도입되기에 이르렀다. 미국에서는 이를 더 발전시킨 Chapman-Richards 함수가 주로 이용되었다. 일부 연구자들은 “일반적으로 유효한 생장법칙이 언젠가는 발견될 수 있을 것이다.” 라고 하였는데, 이는 결국 이루어지지 못한 꿈이 되고 말았으며, 학자들은 아직까지도 생장법칙을 일반성 있게 설명할 수 없다고 말하고 있다(Weiskittel et al., 2011). 그럼에도 불구하고 우리는 생장과정을 설명하기 위하여 이용하는 것이 각종 생물수학적인 통계모델이다.
우리나라에서 본격적으로 생장함수를 이용한 것은 2000년 이후 국가 산림에 대한 임분수확표를 만들면서 임령에 의한 ha당 재적을 추정하기 위하여, Chapman-Richards 함수, Schumacher 함수, Weibull 함수 등을 적용하여, 경험적 수확표를 만들면서 최신·고도화 되었다고 볼 수 있다. 그 외에도 Gompertz, Logistic 함수 등도 도입되어 적용하였으나, 최종적으로는 Chapman-Richards 함수가 재적을 추정하는데, 대부분의 수종에 적합한 것으로 결론지어 진 바 있다(National Institute of Forest Science, 2015)
본 연구에서는 국가차원에서 조사되는 국가산림자원조사의 결과를 이용하여 임상별, 주요 수종별 생장곡선의 변화 패턴을 생장모델을 이용하여 제시하고, 연년생장량의 변화 등을 구명하였으며, 이를 통해 주요 수종별 재적수확 최대 벌기령을 추정함으로서 산주의 산림경영상 의사결정을 지원할 수 있는 근간을 제시해 보고자 하였다.
재료 및 방법
본 연구에 사용된 자료는 제5차 국가산림자원조사(2006∼2010) 표본점 중 임령별 ha당 흉고단면적 이상치를 기각한 13,015개소 표본점 자료를 활용하였으며, 우리나라 산림이 해방까지의 일본 수탈, 6·25 전쟁 및 경제적으로 어려운 시기의 입목 도남벌과 산림녹화시기 등을 고려하여, 현재 50년 이하인 임분(정상적으로 생육하였을 것이라 판단되는 임분)을 대상으로 분석하였다.
임상별 재적추정식 도출에 사용된 표본점은 상기 표본점 중 침엽수 4,222개소, 활엽수 4,954개소, 혼효림 3,839개소 모두를 이용하였으며, 주요 수종별 재적 추정에는 리기다소나무 452개소, 일본잎갈나무 317개소, 중부지방소나무 2,154개소, 굴참나무 628개소, 상수리나무 212개소, 신갈나무 1,273개소의 표본점 자료를 활용하였다.
5차 국가산림자원조사는 기존 전국을 기본계획구별로 나누어 순회하며 조사하던 조사방법과는 다른 전국 단위로 조사하되, 각 기본계획구의 산림을 매년 20%씩 조사하여 5년이 되는 해에 모든 조사가 완료되는 방식이다(Korea Forest Service, 2016; National Institute of Forest Science, 2015). 10년 전의 자료이기는 하나, 임령에 따른 임목 재적생장의 패턴은 대부분 유사하므로 본 결과를 지금 적용함에도 문제가 없을 것으로 판단하였다. 다만, 연평균생장량(mean annual increment, MAI)과 연년생장량(current annual increment, CAI) 등은 최고점에 이르는 시기가 변동이 있을 수도 있으므로 이에 대한 연구가 필요하다.
5차 산림자원조사 자료 중 임령과 ha당 재적생장량과의 관계를 수식으로 적용하였으며, 생장곡선식 중 Chapman-Richards모델, Schumacher모델, Weibull모델 등을 적용시켰다(Chapman, 1961; Clutter et al., 1983; Richards, 1959; Schumacher, 1939). 이들 중 Schumacher모델과 Weibull모델은 일부 수종에서 계수(parameters)를 수렴하지 못한 관계로 추정식으로 적용하기에는 문제가 있다. 세 개의 모델 중 대부분 수종의 재적생장을 설명하는 계수를 표현해 준 Chapman-Richards모델(이하 C-R 모델)이 최적의 생장 추정이 예상되므로 이 식을 모든 수종에 최종 적용시켰으며, 장벌기 벌기령 등을 고려하여 임령을 60년까지 확장시켜 표현하였다.
여기서, Y=임분 재적(m3/ha), age=임령, a,b,c=파라메터
여기에서, C-R 모델의 파라메터 a는 최종도달량 또는 최대가능량을 나타내며, 파라메터 b는 생장량, 생장율과 규제의 파라메터이다. b가 크게 되면 급상승하는 곡선모양이 된다. b값의 범위는 0<b 이지만, 일반적으로 0<b≤1이다. b는 단독으로 의미를 파악하여도 좋으나, c와 결합한 형으로서 생장과정의 특징을 표현할 수 있다. 즉, 파라메터 b/c는 생장곡선의 변곡점, 이를테면 연년생장량 최대 연령에 있어서 생장률을 나타낸다고 알려져 있다(Lee et al., 1996).
입목들의 수고, 직경 및 재적생장은 통상적으로 S자 곡선(sigmoid curve) 형태를 그리면서 생장한다고 알려져 있다. 따라서 산림 내 입목의 생장은 두 개의 변곡점(inflection point)을 갖고 생장하며, 이 변곡점을 적절히 파악하여 산림관리에 활용한다면 수확량 증대, 벌기령 연장 등 경영의 지침으로 삼을 수 있다. 즉, 상층 변곡점의 지연으로 임목생장의 점근선을 늦게 가져 올 수 있으며, 이로 인한 수확량 증대가 유도 가능하다는 것이다(Clutter et al., 1983; National Institute of Forest Science, 2018).
임령별 ha당 재적의 연평균생장량(MAI) 및 연년생장량(CAI)은 C-R 모델을 적용시켜 도출된 임령별 임분재적으로 계산하였다. 즉 연평균생장량은 당해 연도까지의 임분재적을 연수로 나누었으며, 연년생장량은 당해연도의 재적에서 전년도의 재적을 뺀 값으로 계산하였다(National Institute of Forest Science, 2018).
수종별로 단위면적 당 목재수확량이 최대가 되는 벌기령을 재적수확 최대벌기령(rotation of the highest production in volume)이라 하는데, 이는 일반적으로 연평균생장량과 연년생장량이 만나는 지점이므로, 이 두 생장곡선을 도출하여 수종별 벌기령으로 제시하였다. 이 벌기령은 생장량 최고점 부위에서 변화가 크지 않기 때문에 주변의 경제적 상황을 고려하여 10∼20년 빨리 벌채하거나 늦게 벌채해도 재적생산에 큰 영향을 끼치지 않고 목적을 달성할 수 있는 장점이 있는 벌기령이다(National Institute of Forest Science, 2018; Park et al., 1992).
결과 및 고찰
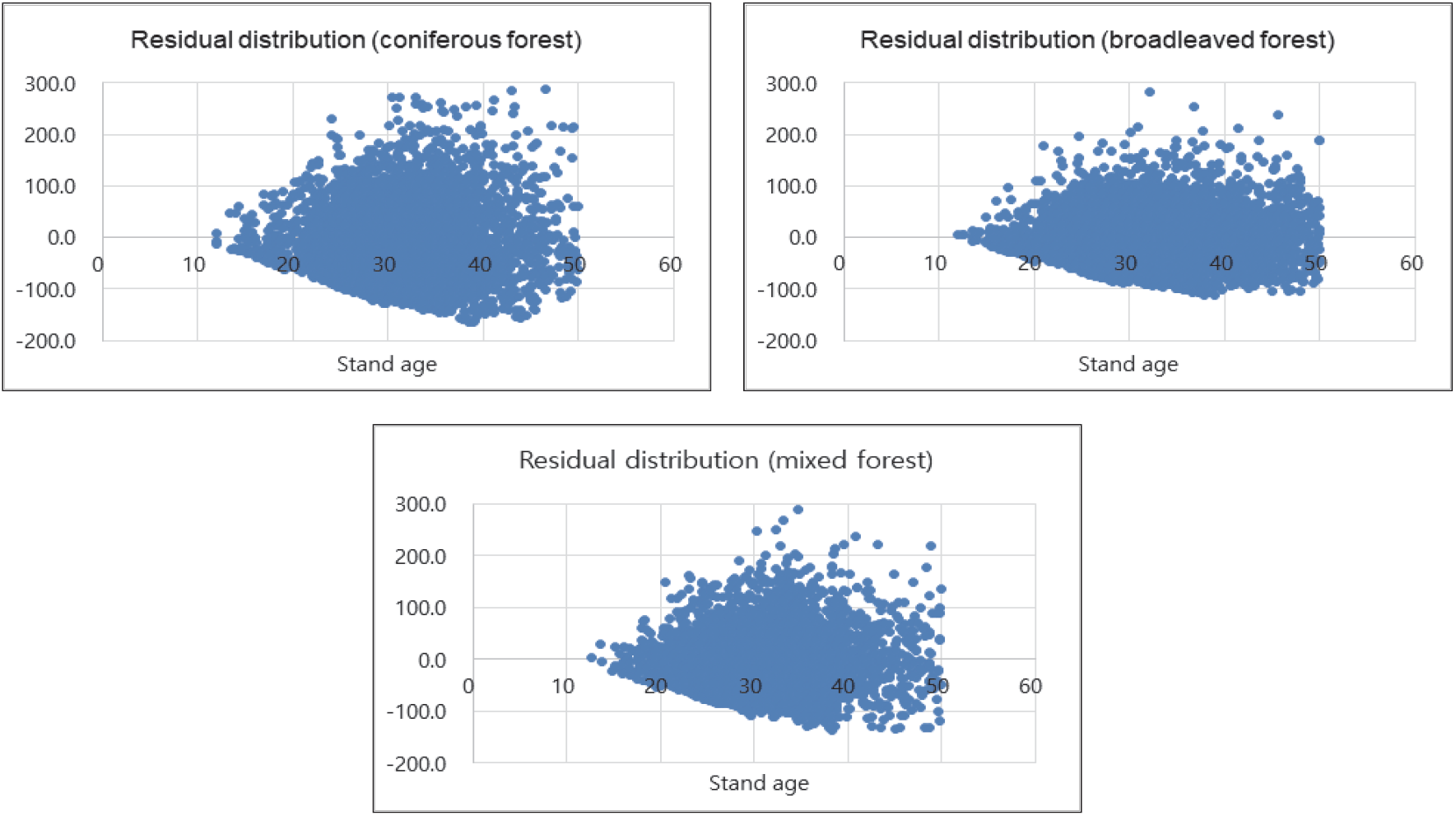
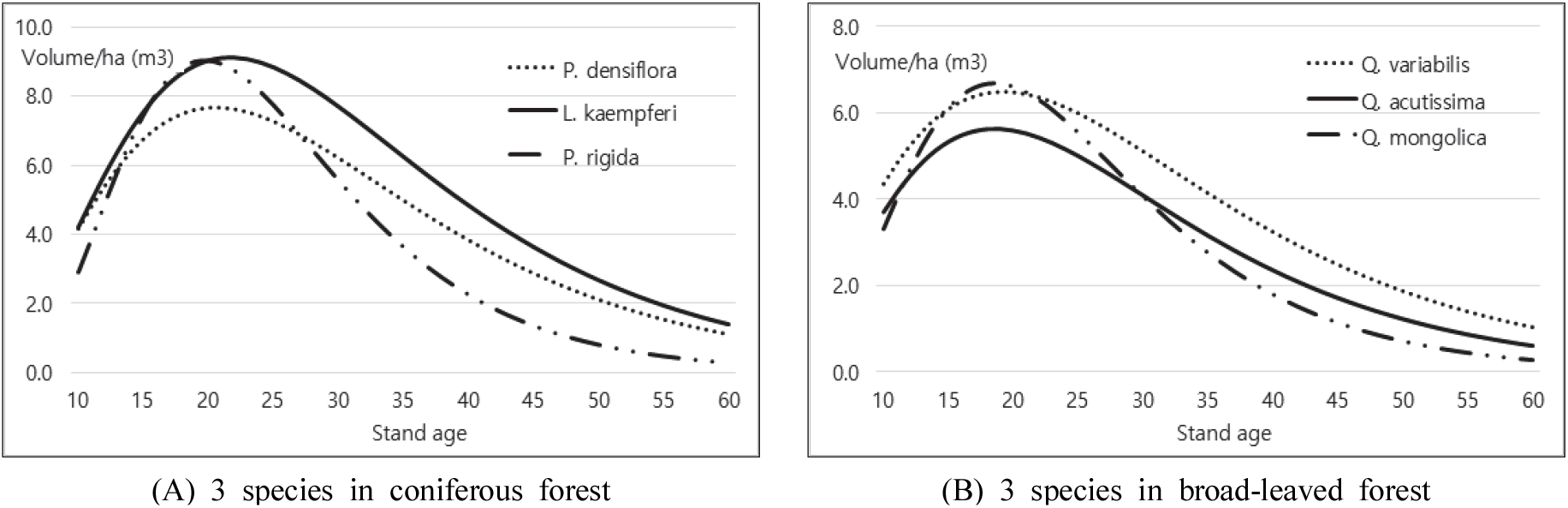
국가산림자원조사 자료를 활용하여 침·활·혼효림으로 나누어 임상별, 임령별로 임목재적량을 C-R 모델로 적용시켜 도출한 결과, 식의 파라메터는 Table 1과 같고, 생장곡선은 Figure 1과 같이 나타났다. 그리고 추정식을 이용하여 실제 표준지별 임분재적을 산출할 수 있는 식(C-R 모델)에 대한 잔차도를 도출한 결과는 Figure 2와 같다.
| Stand types | Parameters | Fitness index | ||
|---|---|---|---|---|
| a | b | c | ||
| Coniferous forest | 251.398 | 0.074 | 4.418 | 0.19 |
| Bread leaved forest | 169.672 | 0.097 | 7.199 | 0.25 |
| Mixed forest | 218.189 | 0.078 | 4.089 | 0.24 |
우리나라 산림에서 임상별로 임령에 따라 침엽수림의 생장량이 가장 높으며, 다음이 혼효림, 활엽수림 순이었다. 임령 60년 정도에 달할 때 우리 산림의 ha당 평균 재적생장량은 침엽수림 238.7 m3/ha, 활엽수림 166.2 m3/ha으로, 침엽수림과 활엽수림 간 최종 수확시기의 재적량은 확연한 차이가 있는 것으로 밝혀졌다(Figure 1).
우리나라 임상별 평균적인 생장곡선 도출을 위해 C-R모델을 적용시킨 결과, 침엽수림을 추정식이 설명할 수 있는 적합도지수(fitness index)는 0.19, 활엽수 0.25, 혼효림 0.24로 비교적 낮게 나타났다(Table 1). 추정식의 잔차분포도는 침엽수림에서 30년 이후에 약간 과소 추정되는 경향이 있었으며, 활엽수와 혼효림에서도 동일한 양상을 보이고 있었다(Figure 2). 추정식에 의한 재적 잔차는 대체적으로 “0”을 중심으로 고르게 분포하고 있는 것으로 나타났는데, 이는 이 추정식이 실측치 y에 대하여 잔차 e 값이 특별히 편의(bias)되거나 이분산성(heteroscedasticity)을 보이지 않았으므로 재적 추정에 C-R모델을 이용함이 타당하다고 유추할 수 있다. 일반적으로 회귀식이 잔차의 왜곡이 있을 경우 변수변환 즉, 로그(log)변환을 취하면 등분산성을 만족시킬 수가 있다.
하나의 지역에 국한하는 생장을 모니터링하는 영구적인 생장표본점(permanent plots)이 아닌 전국을 대상으로 한 임시표본점(temporary plots)의 생장패턴을 하나의 추정선으로 표현하여 설명함은 어려운 일이다. 특히 복잡, 다양한 수종으로 구성되어 있는 침엽수, 활엽수림 및 혼효림을 입지환경인자 즉, 임지생산력을 나타내는 지위를 고려하지 않고, 통합적인 임상별 생장 추정선을 도출하였기 때문에, 임령별 재적 추정선과의 재적 편차의 크기가 다양하여 본 분석에서 적합도 지수가 낮게 나타나게 된 것으로 판단된다. 이러한 경우, 지위지수별로 또는 지역별로 임령(x)과 재적(y)을 카테고리화하여 재적을 추정하는 방법을 이용할 수 있으나, 본 연구의 목적이 전국적인 임상별 재적분포 경향을 파악하고 이를 개괄적으로 추정하기 위한 분석이므로 지위지수별로 구분된 재적 분석 등은 수행하지 않았다.
침엽수림 대표 수종으로는 중부지방소나무(Pinus densiflora), 일본잎갈나무(Larix kaempferi), 리기다소나무(Pinus rigida)를 대상으로 하였는데, 이는 침엽수림 중 수종별 면적분포를 고려하여 선정한 것이며, 잣나무와 같은 경우는 우리나라 대표 수종이기는 하나, 주로 경기, 강원권 일부에 국한되고 있어 제외하였다. 임업통계에 의하면 리기다소나무의 면적은 386,991 ha, 잣나무는 214,357 ha로 보고되었다(Korea Forest Service, 2011).
C-R 모델을 적용한 중부지방소나무, 일본잎갈나무, 리기다소나무의 재적생장 추정식 모수 및 곡선 형태는 Table 2와 Figure 3과 같이 나타났다. C-R 모델이 세 수종의 재적생장을 설명할 수 있는 적합도 지수는 일본잎갈나무가 0.32였으며, 나머지 두 수종은 0.14, 0.18로 아주 낮게 나타났다. 중부지방소나무 등 3개 침엽수종의 재적 추정 적합도 지수가 낮은 원인은 임상별 추정식 도출에서도 언급한 바 있지만, 동일 수종이라 하더라도 다양한 입지와 자연환경, 공간분포(밀도) 등에서 생육하므로, 생육환경에 대한 기준을 정하여 비교함이 적합도를 높일 수 있었을 것이다. 즉, 동일 중부지방소나무라 하더라도 지위지수를 산출하여, 동일 지위지수를 갖는 표본점 자료 내에서 재적 추정식을 도출하는 것이 추정의 적합도를 높일 수 있는 방법으로 판단된다.
| Species | Parameters | Fitness index | ||
|---|---|---|---|---|
| a | b | c | ||
| P. densiflora | 261.083 | 0.070 | 4.065 | 0.14 |
| L. kaempferi | 311.008 | 0.071 | 4.450 | 0.32 |
| P. rigida | 209.850 | 0.110 | 8.247 | 0.18 |
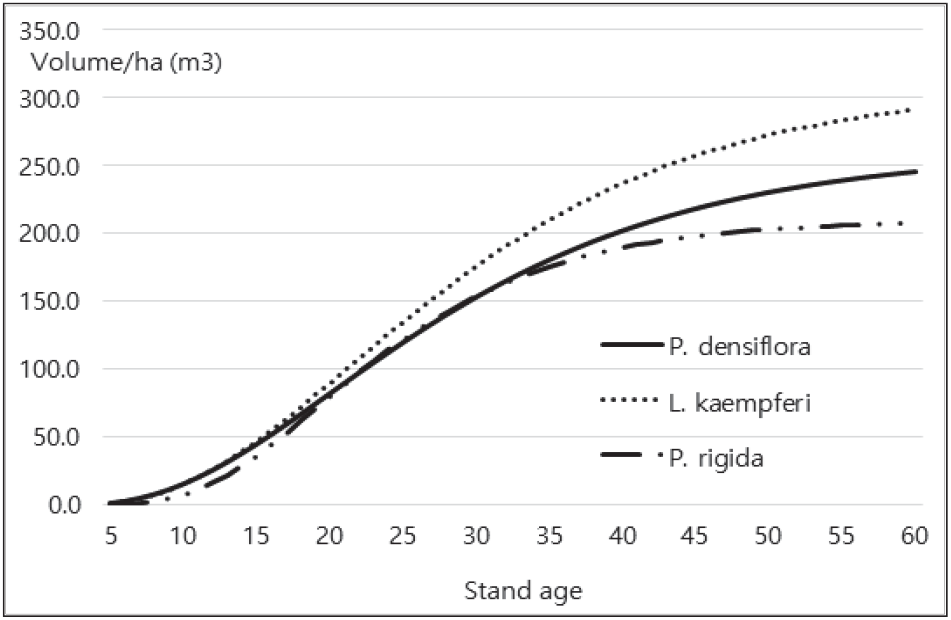
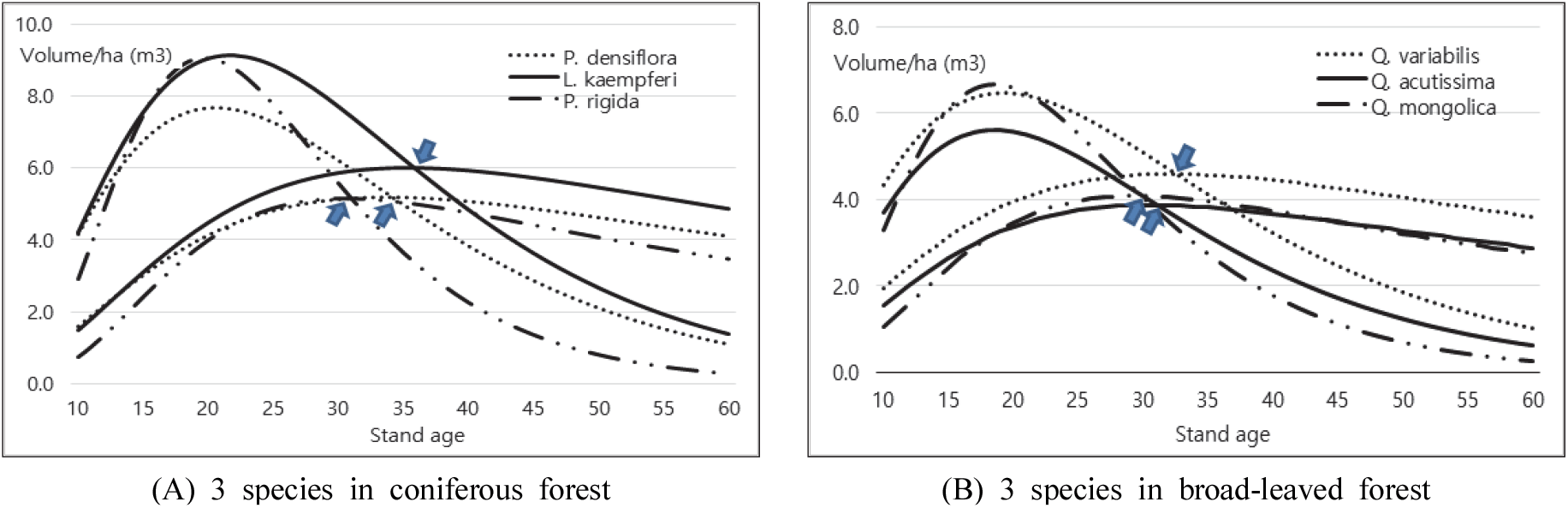
Figure 3에서 일본잎갈나무의 연차별 생장이 가장 높음을 알 수 있었으며, 임령 60년이 되면 약 290 m3/ha의 재적수확이 예상된다. 그리고 중부지방소나무와 리기다소나무는 30년까지는 생장패턴이 유사하였으나, 이후 리기다소나무가 빨리 생장의 변곡점을 갖는 것으로 나타나, 임령이 60년에 이르면 중부지방소나무의 최종 수확량이 리기다소나무 보다 약 40 m3/ha 정도 높을 것으로 예상된다.
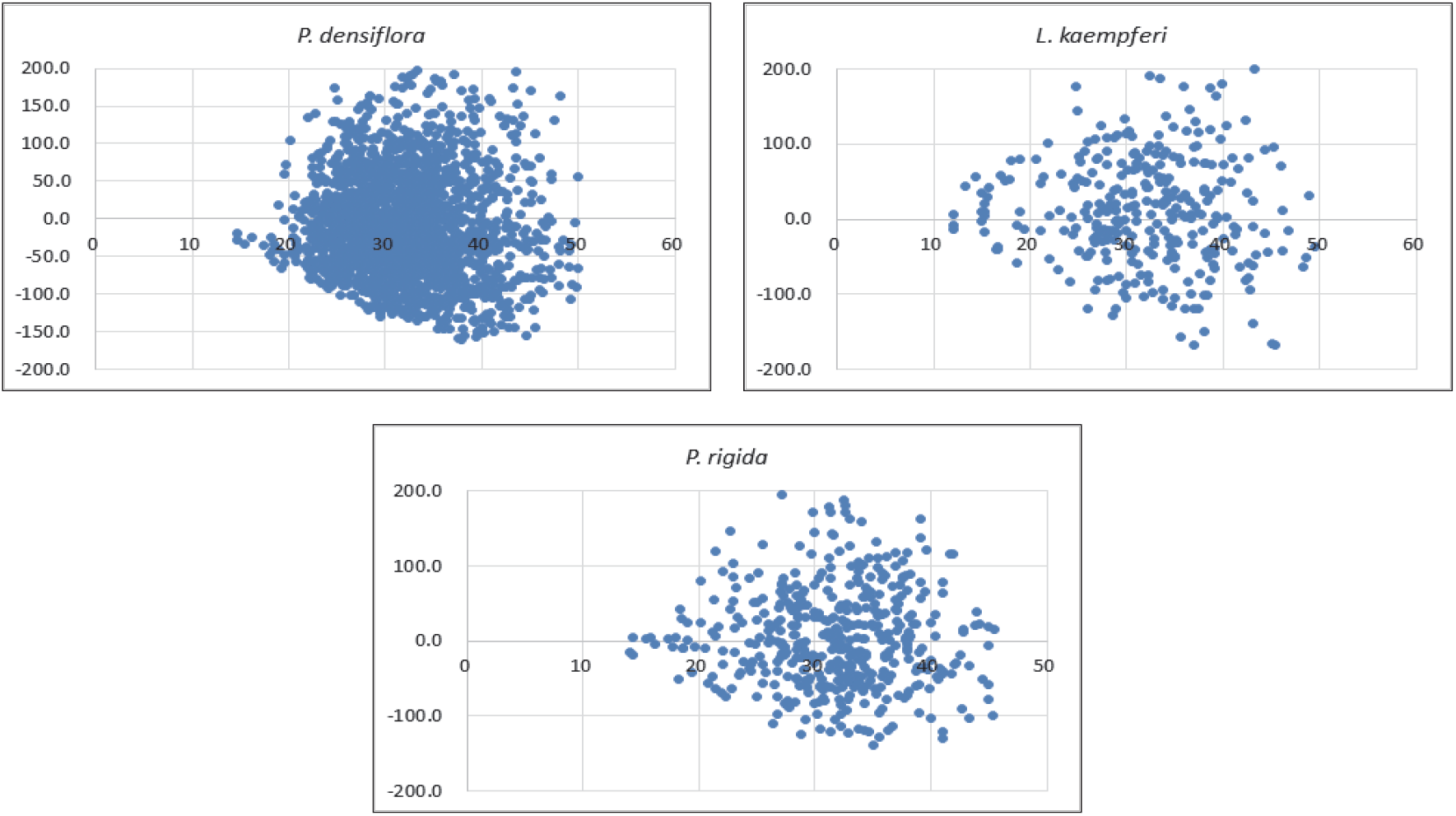
이들 세 수종의 재적생장을 예측하는 C-R모델의 잔차도는 Figure 4와 같고, 일본잎갈나무를 제외하고는 모두 20년 이후부터 과소 추정값을 갖는 것으로 나타났다. 추정식의 재적추정 적합도지수가 낮으나 잔차도가 전반적으로 “0”을 중심으로 대부분 분포하고 있어, 세 개 임분의 재적생장을 추정하는데 적합한 것으로 판단된다. Son et al. (2014)의 연구에서도 삼나무 재적추정식 도출에서 추정식에 대한 적합도지수가 낮은 경향을 보였는데, 이는 자연상태에 있는 임목의 생장을 설명할 수 있는 정확한 추정식은 결코 만들어지지 않을 것이라는 연구결과를 뒷받침해 주는 것이라 볼 수도 있다(Weiskittel et al., 2011).
우리나라 활엽수림은 참나무림이 대부분 군락으로 우점 분포하고 있으므로 이중 분포면적을 고려하여 굴참나무(Quercus variabilis), 상수리나무(Quercus acutissma), 신갈나무(Quercus mongolica)를 대표 수종으로 하여 C-R모델을 적용시켜 생장량을 추정한 바, 식의 적합도지수는 0.22 이하로 낮게 나타났다(Table 3). Son et al.(2015)은 자연상태의 아까시나무 재적 추정에서 식에 대한 적합도지수가 낮게 나타났다고 보고하였는데, 적합도지수가 낮은 원인은 침엽수 주요 수종별 생장량 추정 부분에서 언급한 바와 같다. 다만 국가산림자원조사가 전국에 배치시킨 영구표본점을 조사한 자료이므로 우리가 원하는 즉, 정상적인 생육상태를 보이는 곳을 대상으로 임의로 우리가 조사할 수 있는 여건이 아니기 때문에, 상기의 지위지수를 고려한 재적 추정식 분석도 높은 적합도지수를 도출하지 못한 것으로 판단된다.
| Species | Parameters | Fitness index | ||
|---|---|---|---|---|
| a | b | c | ||
| Q. variabilis | 231.730 | 0.064 | 3.325 | 0.21 |
| Q. acutissima | 180.944 | 0.073 | 3.726 | 0.22 |
| Q. mongolica | 167.310 | 0.099 | 5.996 | 0.17 |
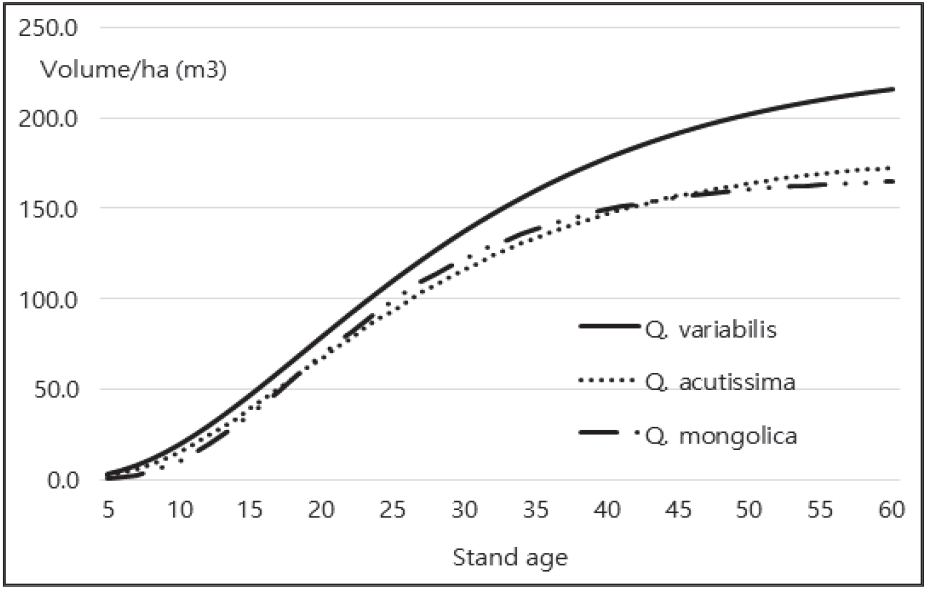
활엽수 세 수종 중 굴참나무의 생장이 가장 우세하였으며, 상수리나무와 신갈나무는 생장 패턴이 유사하나, 60년생 정도가 되면 상수리나무의 총 생장량이 신갈나무를 앞 설 것으로 예상된다. 그러나 주요 침엽수림 세 개 수종과 비교할 때는 참나무림의 생장량이 다소 낮게 나타남을 알 수 있었다(Figure 5).
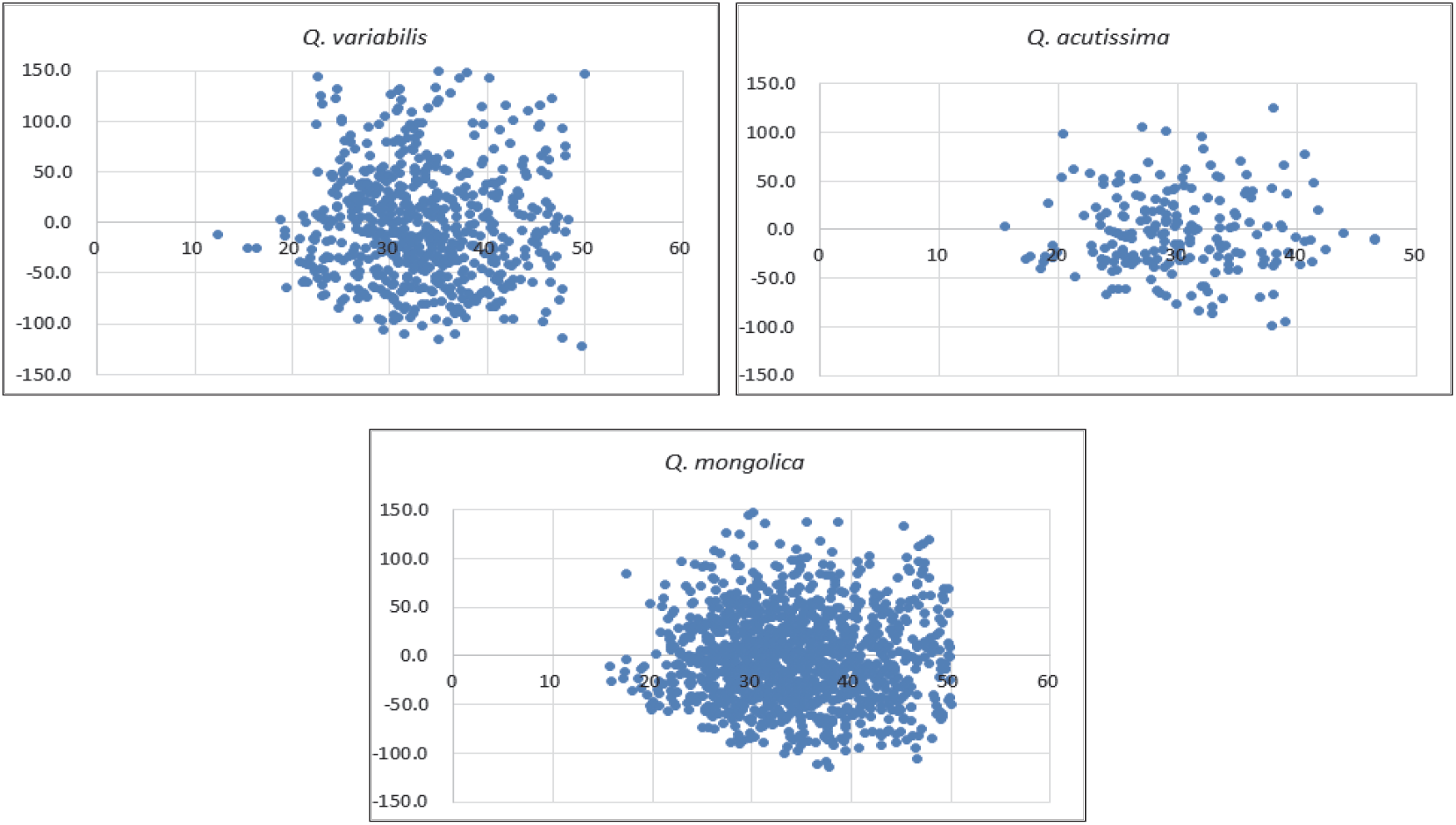
이들 세 수종의 C-R 모델에 의한 잔차도는 Figure 6과 같이 나타났으며, 상수리나무를 제외한 두 수종의 추정식이 일부 표본점에서 약간 과소 추정되는 잔차를 보이고 있었다. 그러나 추정식의 적합성 및 활용 가능성을 알 수 있는 잔차가 침엽수 세 수종 잔차와 마찬가지로 “0”을 주변으로 대체적으로 고르게 분포되어, 이들 식을 활엽수 세 수종 재적추정식으로 활용할 수 있을 것으로 판단된다.
임목은 무한히 생장할 수 없으며, 초기생장은 급속도로 이루어지다가 말기에 이르면 생장이 둔화되는 전형적인 “S”자 곡선을 그리면 생장하게 된다. 따라서 연평균생장이 최대가 되는 시기는 생각보다 일찍 오게 되는데, 수종별로 차이는 있으나 대체적으로 임령 30년 전후가 된다(National Institute of Forest Science, 2015).
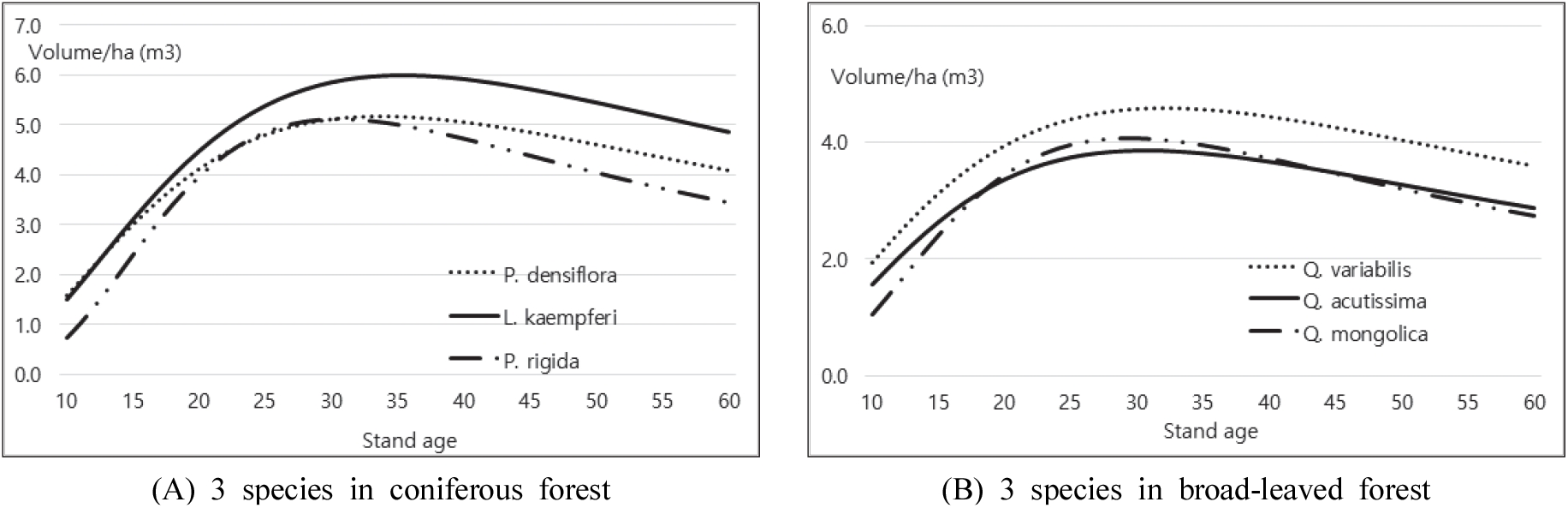
침엽수 및 활엽수림에서 각각 주요 세 수종의 재적생장량 변화에 있어 임령에 따른 최고의 재적 생장점을 갖는 위치인 연평균생장량을 도출한 결과는 Figure 7과 Table 4와 같다. 연평균생장량은 침엽수 중 중부지방소나무는 34년, 일본잎갈나무 35년, 리기다소나무 31년으로, 침엽수는 평균 33년에 이를 때 최대시기에 도달하는 것으로 나타났다. 그리고 활엽수는 굴참나무 32년, 상수리나무 30년, 신갈나무 29년으로 평균 30년일 때가 최대시기임을 알 수 있었다. 여기에서 각 수종별로 생장곡선의 점근이 늦게 나타날수록 MAI 최고지점(변곡점)도 임령이 늦게 형성됨을 알 수 있었다. 이 같은 결과는 국립산림과학원(National Institute of Forest Science, 2016)에서 발표한 현실림 임분수확표 상 지위 ‘중’의 연평균생장량과 유사한 결과이다. 그리고 신갈나무는 해발고가 다소 높은 지대에 생육하여 국소적인 또는 기상적인 문제로 생장량 최대의 시기가 빨리 도래하는 것으로 판단된다.
MAI의 패턴이나 형성되는 최고지점을 구명에 따라 조림, 시업 및 환경인자 등을 조절할 수도 있을 것이며, 여기에서 파생되는 임목 생장량의 극대화 및 수확시기 등이 바뀔 수도 있어, MAI 정보 도출은 산림경영에 지대한 영향을 가져 올 수 있는 인자이다.
정기생장량(periodic growth increment, PGI)은 일정 기간 내 생장한 임분재적량을 그 기간의 연수로 나누어 준 것으로, 보통 5년을 주기로 하며, 1년 단위로 하면 연년생장량(CAI)이 된다. 다만 이는 평균적인 값이 되므로, 실제적인 계산은 당해년도의 재적값에서 전년도 재적값을 뺀 것이 CAI가 된다.
Figure 8에서 연년생장량이 최고가 되는 지점은 침엽수는 20∼22년, 활엽수는 19년에서 형성되고 있다. 이는 앞서 언급한 바 있듯이 전년도 대비 당해연도에 재적이 어느 정도 생장했는지를 나타내는 척도이다.
수종별로 재적수확이 최대가 되는 벌기령은 MAI 최대시기와 CAI가 만나는 지점으로 판단할 수 있다. 물론 MAI 최대시기로서 벌기령을 정할 수도 있지만, CAI를 활용하는 것이 보다 정확한 판단이 될 수 있다.
각 수종별로 재적수확 최대벌기령은 Figure 9와 같이 도출되었다. 일본잎갈나무는 벌기령 최적시기가 35년으로 나타났는데, 현재 산림청(Korea Forest Service, 2014)의 벌기령 기준(공·사유림)은 30년으로 이와 유사한 시기로 결정되어 있다. 그리고 참나무류는 25년을 기준 벌기령으로 삼고 있는데 본 연구에서는 굴참나무 등 3수종 평균 벌기령이 30년으로 나타나, 현재 벌기령과 별 차이가 없음을 알 수 있었다. 한편 국유림의 경우는 장벌기 대경재 생산을 목적으로 하므로 현재 기준벌기령은 일본잎갈나무 50년, 참나무류 60년으로 정해져 있다.
또한 산림청에서 신설한 벌기령 가운데 기타활엽수의 경우, 40년을 기준으로 하고 있는데, 기타 활엽수가 혼재하여 생육하고 있는 혼효림의 MAI를 계산해 보면, 34년이 최대시기로 나타나, 이 역시 몇 년 차이가 나지 않음을 알 수 있었다. 따라서 현재 산림청의 벌기기준령과 본 연구에서 도출된 재적수확 최대 벌기령 간 차이가 없어, 산림정책 자료의 뒷받침해 주는 근거 자료로 활용될 수 있을 것으로 본다.
결 론
임목의 생장은 시간이 지남에 따라 생장을 하나 무한한 것은 아니며, 일정한 법칙에 의해 생육하고 있다. 즉, 학자들은 대부분의 임목이 S자 곡선(sigmoid curve)를 그리면서 생장함은 밝혔으나, 이를 설명할 수 있는 수확식 제시가 미흡한 실정이다.
본 연구에서는 침엽수 중 중부지방소나무, 일본잎갈나무, 리기다소나무, 그리고 활엽수는 굴참나무, 상수리나무, 신갈나무 등을 대상으로 국가산림자원조사를 활용하여 재적생장 패턴을 알아보고, 또한 이를 이용하여 연편균생장량 및 벌기령까지를 구명하고자 하였다. 그러나 재적생장을 표현할 수 있는 현재의 몇 가지 수학식을 적용한 결과, 이 식이 재적생장 패턴을 어느 정도 설명할 수 있는 지 알 수 있는 적합도지수 값이 비교적 낮게 나타났다. 다만 식의 잔차도를 분석 한 결과, 이 식이 수종별로 “0”을 주변으로 임령에 따라 대체적으로 고르게 분포하고 있어, 현재로서는 이를 우리나라 현실림에 대한 수종별 생장패턴을 설명하는 식으로 활용 가능한 것으로 판단된다.
산림 내에서 임목생장을 고정표본점이 아닌 임시표본점의 자료를 활용하여 생장상태를 구명하고 이를 수식화 하는 것은 결코 쉬운 일이 아닐 것이다. 임목이 자라는 토양환경과 국소지역에 따른 기상의 차이, 그리고 일부 인간 간섭에 따른 임분밀도의 변화 등을 하나의 식에 담아 설명함은 불가능한 일로 보인다. 향후 지금껏 배치되어 지속적으로 조사되고 있는 국가산림자원조사 표본점과 학술 목적으로 설치된 다양한 고정표본점의 자료를 활용한다면 우리 산림에 적용할 수 있는 고유의 생장 수학식을 만들 수 있을 것으로 판단된다.
재적수확 최대벌기령의 경우, 현재의 수종별 생장패턴으로 보았을 때는 약 30년 정도에서 형성되나, 생장의 sigmoid curve의 두 번째 변곡점을 늦출수록 재적수확량 증가와 보다 우량의 대경재 생산이 가능할 것으로 예측되므로 향후 이에 대한 연구도 필요할 것으로 생각된다.