서 론
아까시나무(Robinia pseudoacacia L.)는 북미가 원산지인 나무로서, 우리나라에는 1900년대 초 용산구와 경인선 철로변에 처음 심게 되었다고 전해지며, 철로변에 심게 된 이유는 이 나무가 재질이 강인하고 내구성이 매우 크기 때문에 철도침목용으로 사용하기 위해서였다고 한다(The Forest Experiment Station, 1925). 또한, 아까시나무는 일본의 우리나라 강점기에 황폐된 산지의 복구와 연료림 조성을 목적으로 식재가 권장되어 1930~40년대 집중 식재가 되었으며, 해방 이후의 혼란한 시기와 6.25 전쟁을 거치면서 극도로 헐벗게 된 산지를 녹화시키고, 국민들의 취사 및 연료의 안정화, 그리고 산지 사방용으로 다시 아까시나무의 재조림 붐이 대대적으로 일어나게 되었다(Lim, 1994). 1960~1967년까지 약 13억 그루가 조림되었으며, 그 이후 조림이 대폭 줄었으나, 1978년말 까지 누적합계로는 약 16억 그루, 면적 32만ha에 조림이 이루어진 것으로 나타난다(Kim, 1993).
아까시나무는 목재기본밀도가 0.74 g/cm3로서 다른 속성수인 이태리포플러(0.34 g/cm3)와 오리나무(0.52 g/cm3)보다 2~3배 높아 탄소중립 시대를 맞아, 그리고 전통적인 꿀샘식물(밀원식물)로서 다시 각광을 받을 수 있을 것으로 기대된다(Jung et al., 2009; Park, 1997, 2008; Son et al., 2014). 특히 Son et al.(2014)에 의하면, 아까시나무 임분의 연간 이산화탄소흡수량이 13.79 tCO2/ha/yr이라고 밝혀, 온실가스 흡수량이 가장 높다고 알려진 참나무류(12.1 tCO2/ha/yr)와 비교하여도 더 높아 기후변화에 대응할 수 있는 주요한 수종이라 볼 수 있다.
최근 자료에 의하면, 아까시나무의 꿀 생산량은 전체 양봉산업의 70%를 차지하며, 연간 약 1,000억원의 소득을 농민에게 가져다주는 효자 꿀샘식물로 자리매김하고 있으나, 기후변화에 따른 아까시나무 꽃의 개화 흉·풍년, 생육 쇠퇴 등에 따라 산림청에서는 아까시나무의 품종 개발(Korea Forest Service, 2021) 및 백합나무, 헛개나무, 쉬나무 등의 대체 자원에 대한 조성계획도 수립·시행하고 있다(Korea Forest Service, 2016). 또한, 농림축산식품부는 「양봉산업의 육성 및 지원에 관한 법률」을 제정하여, 2020년 8월 28일부터 시행하고 있어 양봉산업의 안정적이고 지속적인 성장을 지원·도모하고 있다.
아까시나무는 척박한 땅에서도 잘 자라는 것으로 알려져 있으나, 이는 사방 또는 산림녹화를 이야기할 때의 조림계획에 적용할 수 있을 것이며, 어떠한 나무라도 비옥한 땅에 잘 자랄 것이므로, 이제는 적지적수(suitable tree on the site) 및 지위지수(site index)의 개념이 들어 있는 조림계획이 요구되는 시대라 할 수 있다.
지위지수는 적지적수를 판정할 수 있는 도구로서, 세계 각국은 수종별로 지위지수를 추정하기 위하여 많은 모델을 개발하여 이용하고 있으며, 현재 이들 중 가장 많은 이용빈도를 보이는 모델은 Chapman-Richards모델과 Schumacher모델이다(Chapman, 1961; Richards, 1959; Schumacher, 1959). 국내에서는 지위지수는 일반적으로 30년생 기준의 우세목 수고로서 표현되며, National Institute of Forest Science(2016)은 소나무 등 침엽수 8종, 굴참나무 등 활엽수 6종에 대한 지위지수를 도출하고 분류곡선을 제시한 바 있다. 지위지수 정보는 산림경영자에게 각 수종들에 대한 현재의 입지 상태와 임지생산력을 평가, 제공할 수 있으며, 향후 조림지에 대한 적지적수를 판정할 수 있는 유용한 정보가 된다.
아까시나무에 대한 지위지수 정보는 Son et al.(2014)이 잠시 언급한 바 있으나, 당시는 잠정적인 연구 정보였으며, 본 연구는 아까시나무의 생육지(어린 임분 대상) 추가 조사, 기존 표준지 조사 자료 재검토, 자료의 이상치 기각 등을 통해 현실을 반영한 지위지수 결과를 제시하고자 하였다. 또한, 적지적수된 아까시나무는 상대적으로 가지의 발달이 우세하여 꽃 생산량의 증가가 기대되므로, 지위지수별 직경급 분포가 어떻게 변화하는지를 제시하여, 향후 아까시나무 조림지 선택을 위한 정보 제공차원에서 본 연구를 수행하게 되었다.
재료 및 방법
아까시나무에 대한 생장정보를 확보하기 위하여 국가산림자원조사(National Forest Inventory, NFI) 시의 표준점 자료, 국립산림과학원 고정수확시험지 자료(광릉) 및 일부 유령림에 대해서는 직접 현지에서 임시표본점을 설치하여 Table 1과 같이 표준지 생장정보를 획득하였다. 국가산림자원조사 자료는 자연적 피해지, 나지에 위치한 표준지, 인위적 훼손지 등에서 획득한 자료는 아까시나무 생장에 대한 대표성을 상실하고 있으므로 분석에서는 제외하였다. 그리고 아까시나무 표준지는 대부분 경남북, 충청권 및 경기 남부권에 위치하고 있었으며, 타 수종이 혼효된 표준지에 대한 대표 수종으로서의 선발은 NFI지침에 의해 흉고단면적 비가 50%이상인 수종으로 정해졌으며, 이들 자료를 활용하였다. 한편, 국립산림과학원에서 설치한 아까시나무에 대한 고정수확시험지는 1970년대 설치한 것으로 그 규모는 0.1 ha 이상으로 조성되어 있으며, 현재는 속성수의 노령화로 인하여 많은 부분이 고사하였으나, 본 분석에서는 5년간 주기적으로 조사한 결과(야장)를 활용하였다.
| Growth factors | No. of plots | Age (year) | Stand density (trees/ha) | DBH (cm) | Height (m) |
|---|---|---|---|---|---|
| Species | |||||
| Robinia pseudoacacia | 169 |
지위지수를 구명하기 위하여 적용된 모델은 국립산림과학원(2016)에서 국가산림자원조사 자료를 이용하여 우리나라 현실림의 경험적 수확표를 만들 때 적용한 모델로, Chapman-Richards height/age function(이하 C-R모델)이고, 모델의 형태 및 모수(parameters)는 다음 식 1과 같다. Schumacher모델에 비하여 이 모델은 지위지수 곡선을 융통성 있게 표현해 주며, Schumacher모델은 지위지수가 다소 직선적일 때 잘 설명해 준다고 볼 수 있다.
그리고, 분석에 있어 자료의 적합성을 검증하기 위하여, 실제 분석에 적용한 자료(fitted data)와 검증 자료(validation data)로 구분하고, 전체 자료를 70:30으로 나누어서 통계적 검증처리를 수행하였다.
(여기에서, SI: site index, HD: dominant tree height, ti: stand age, tj: base age(30), b & c: parameter)
C-R모델은 본래 3개의 모수를 가지고 있으나, 모수(a)를 최고 값을 나타내는 점근(asymptotic)값인 우세목의 수고(HD)로 대체한 모델이다. 이 모델의 모수 b는 시간(t)축의 크기를 결정하고, c는 생장곡선의 모양에 관계되는 모수이다(Clutter et al., 1983). 그리고 지위지수를 추정할 수 있는 이 모델은 우세목 수고가 30년일 때를 기준으로 하였는데, 30년은 일반적으로 sigmoid 형태를 갖는 수고 생장 곡선이 거의 정점에 이르는 때이며, 이어서 점근화되는 경향이 있기 때문에 기준임령(base age)을 30년으로 설정한 것이다. 또한, 재적생장에 있어서도 보통 30년 전후가 되면 연평균생장량(Mean annual increment, MAI)이 정점에 이르고 이후는 낮아지기 때문에 30년을 적용한 측면도 있다. 그리고 현재 National Institute of Forest Science (2016)에서 발간한 임분수확표에서도 지위지수의 기준임령을 30년 사용한 바 있다.
산림 내 직경분포 연구 초기에는 변형된 형태의 정규분포와 Gamma 확률밀도함수를 이용하였지만, 다양한 직경분포를 갖는 현실림의 적용에 있어 다소 문제점이 있었다(Shin et al., 1998). 1965년 Clutter와 Bennet가 적용한 Beta함수는 천연림의 직경분포 추정에 문제점을 갖고 있었고, 또한 추정해야 할 모수가 많은 것이 문제점이었다(Yun et al., 1991). 그 후 Bailey and Dell(1973)은 공학 분야에서 제품의 수명분포를 설명하기 위해 Weibull(1939)에 의해 제안된 Weibull함수를 임분직경분포 추정에 이용함으로서 이러한 문제점을 해결하였다.
한편 Weibull 함수의 모수 추정은 백분율법(percentile method) 등 다양한 방법이 사용되고 있으나(Borders et al., 1990), Garcia(1981)가 단순적률법(simplified method-of-moments)으로 간단하게 계산할 수 있는 방안을 제시한 바 있다. 이 방법은 최소직경, 평균직경, 직경의 표준편차 등에 의해 쉽게 모수를 추정할 수 있으며, 최소직경과 직경의 표준편차는 평균직경과 우세목 수고에 의해 추정이 가능하다.
본 연구에서 적용된 Weibull 확률밀도함수 형태는 식 2와 같으며, 이 함수는 3개의 모수를 갖는다.
여기서, x는 흉고직경, a, b, c는 모수. a는 직경분포의 범위, b는 직경분포곡선의 모양, c는 최소직경을 결정한다.
본 연구에서는 아까시나무 임분 표준지 내 임목에 대한 흉고단면적의 Weibull 분포 모수를 최소흉고단면적, 평균흉고단면적 및 흉고단면적의 표준편차로 추정하였으며, 이로서 추정된 흉고단면적분포를 다시 흉고직경분포로 전환하였다. 이런 전환 절차를 거친 것은 우리가 일반적으로 예측하고자 하는 재적(m3)은 3차원인 데 비해, 흉고직경은 1차원(cm)이며, 흉고단면적(cm2)은 이보다 가까운 2차원이기 때문이다(Lee et al., 2003). 다음은 평균직경과 우세목 수고에 의해 최소직경과 흉고단면적의 표준편차에 대한 추정식을 도출하였으며, 각 표준지에 대해 평균흉고단면적(평균직경에서 계산)과 개발된 추정식에서 얻은 최소흉고단면적(최소직경으로부터 계산) 및 흉고단면적의 표준편차를 가지고 단순적률법에 의해 흉고단면적 Weibull 분포 모수를 추정하였다. 즉, 각 표준지의 평균직경과 우세목 수고 등 일반적인 임분매목조사 시 얻게 되는 임분생장 특성에 의해 Weibull 직경분포의 모수를 복구(parameter recovery) 하였으며, 이를 이용하여 아까시나무에 대한 임분 직경분포를 추정하였다(Son et al., 2004, 2006).
Weibull 직경분포의 모수 추정 및 적합에 대한 통계적 검정은 Kormogorov-Smirnov검정법 (5% 유의수준)을 사용하였으며(Garcia, 1981), 통계분석 프로그램은 SAS(6.12)였다.
결과 및 고찰
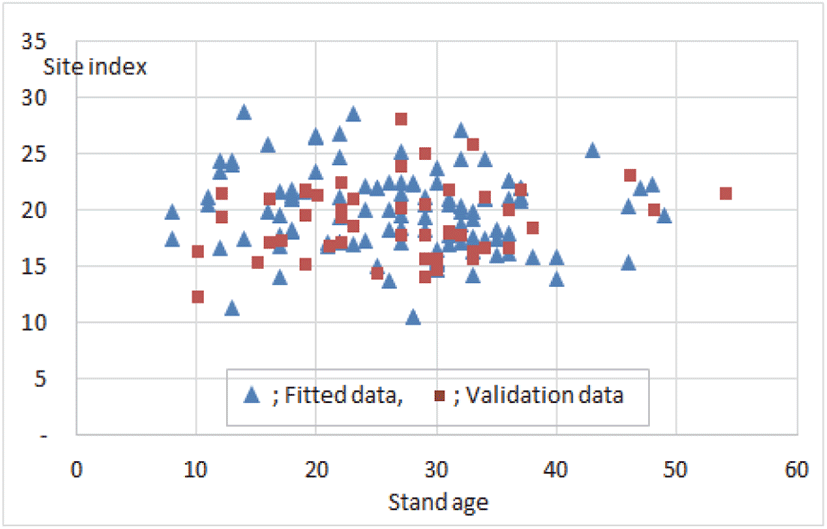
전체 표준지 자료 169개 중 실제 분석에 적용한 자료(fitted data) 118개와 검증을 위하여 51개 표준지를 구분하여, 적용자료에 대한 지위지수 추정식을 도출하고 이를 검증자료에 적용한 결과 Figure 1과 같았다.
Figure 1을 보면 실제 분석에 적용한 자료를 이용하여 도출한 지위지수 추정식이 검증자료에 사용함에 문제가 없음이 나타났으며, 두 집단간의 T-test 결과도 1% 유의수준에서 집단간 차이가 없는 것으로 나타나 본 분석에 사용한 자료의 신뢰성을 입증해 주었다.
자료의 적합성에 대한 검증이 완료된 전체 표준지 자료(168 plots)를 이용하여, 표준지 임령을 독립변수로, 우세목 수고(정상적인 직경급을 보이면서 생장한, 폭목을 제외 한)를 반응변수로 하는 비선형방정식인 C-R 모델을 활용하여 지위지수 추정식의 모수 및 생장값을 도출한 결과 Table 2와 같다.
| Model | Parameters | Fitness index | Bias | |
|---|---|---|---|---|
| b | c | |||
| 0.051038 | 0.759639 | 0.3695 | −0.0030 | |
Table 2를 보면, 지위지수를 추정할 수 있는 식에 대한 적합도 지수(fitness index)는 약 37% 정도로 나타나서 약간 낮은 값이라고 볼 수 있으나, 이는 다양하게 분포하는 우세목의 수고 값의 가운데를 통과하는 하나의 선에 대한 통계치로 크게 의미를 부여할 필요는 없다. 다만 중앙을 통과하는 선에 대한 편의(bias)가 거의 “0”에 가까운 값(−0.0030)을 가지므로, 이 선이 한쪽으로 치우치지 않아, 이를 중심으로 지위지수 선을 배분함이 타당함을 증명해 준다고 볼 수 있다.
또한, 도출된 지위지수 추정식의 모수들 간 점근상관행렬(asymptotic correlation matrix) 계산 결과, 우세목의 수고가 1일 경우, 파라미터 b, c는 각각 −0.9658, −0.8725 로 도출되어, 우세목의 수고와 모수 b, c는 서로 “음(-)의 상관”을 가져 반대 성향이 있음을 알 수 있었다. 이때 모수 b, c 간은 0.9651 값을 가지는 것으로 나타나 고도의 “양(+)의 상관” 관계임을 알 수 있었다.
그리고 지위지수 추정 결과에 따라 우리나라에 생육하는 아까시나무의 지위지수 분포는 다음 Table 3과 같이 나타났다.
| Variable | No. of plots | Mean | Maximum | Minimum | Standard deviation |
|---|---|---|---|---|---|
| Site index | 169 | 19.32 | 28.50 | 10.54 | 3.54 |
| Dominant tree height (m) | 18.08 | 27.80 | 6.90 | 4.13 |
(Note) Base age: 30 years
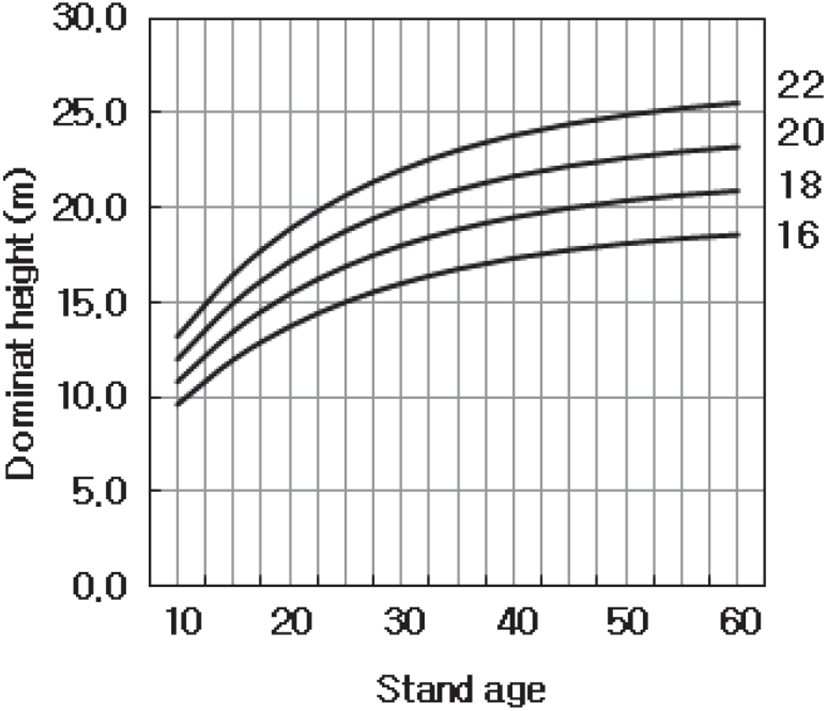
Table 3에서 지위지수의 평균, 최대, 최소값 등은 기준임령을 30년으로 정하여 우세목의 수고로 다시 계산하였기 때문에, 기존 우세목 수고 값과는 다른 분포를 가짐은 당연한 일이다. 여기에서 주목해야 할 것은 지위지수의 분포인데, 평균값이 19.32이고 표준편차가 3.54라 함은, 우리나라 아까시나무의 지위지수 선의 분포가 상한선이 22.86, 하한선이 15.78 이 된다는 의미이다. 따라서 지위지수 최대값이 28.50, 최소값이 10.54라고 해서 지위지수 선을 10부터 28까지 긋는 것은 정상적인 지위지수 범주를 벗어나는 것이므로 주의해야 할 것이다. 물론 특수한 입지에서 지위지수가 극단적인 값을 나타낼 수 도 있을 것이나, 일반적인 경우 우리나라 아까시나무의 지위지수는 2 m로 간격을 둘 때, 22, 20, 18, 16으로 표현할 수 있다. National Institute of Forest Science(2016, 2021)에서 참나무류의 현실림에 대한 지위지수를 추정한 것을 보면, 상수리나무는 지위지수의 범위가 14~20, 굴참나무와 신갈나무는 10~16으로 나타나, 상수리나무와 일부 유사한 경향을 보이고 있으며, 국내에 분포하는 아까시나무가 참나무류보다는 수고생장이 우세함을 유추할 수 있었다.
아까시나무 지위지수분류표 즉, 임령별 일정 우세목 수고값을 가질 때 판정할 수 있는 지위지수를 나타낸 것이 Table 4이다.
예를 들어, 25년생 아까시나무림에서 우세목 수고가 14.8 m라고 한다면, 이 지역의 지위지수는 16이 되며, 우리나라 아까시나무림 전체를 대상으로 한다면, 임지생산력이 아주 낮은 지역이라고 볼 수 있다. 상대적으로 동일 조건에서 20 m 이상의 우세목 수고를 갖는 지역이라면, 지위지수가 최상인 22 이상이므로 아까시나무가 생육할 수 있는 최적의 입지를 갖는 지역이라고 할 수 있을 것이다. 따라서 이 분류표를 이용하면 아까시나무 조림 시 적지적수를 충분히 적용할 수 있을 것이다.
Figure 2의 지위지수 분류곡선 역시 아까시나무 조림을 위한 또는 현재의 입지 판정을 위하여 활용될 수 있으며, National Institute of Forest Science(2016)에서 발간한 “현실림 임분수확표” 상의 속성수 백합나무 지위지수 분류곡선도와 초기, 장령기 및 노년기의 생장패턴이 다소 유사한 경향을 갖는 것으로 나타났다.
아까시나무 임분의 흉고단면적분포를 적합시키기 위하여 이용된 독립변수는 최소흉고단면적, 평균흉고단면적, 흉고단면적표준편차 등이며, 분석에 따라 함수의 모수가 각 표준지별로 도출되었으며, 수종별로 이들 추정치의 범위는 Table 5와 같다. 각 모수의 추정치 범위(최대값, 최소값)로 볼 때 수종별로 직경분포 곡선이 아주 다양함을 알 수 있다. 이러한 것은 아까시나무가 인공적으로 조림이 되었다 할지라도 모수(母樹)가 고사한 후 발생하는 맹아들이 자유롭게 생장하기 때문에 타 인공림보다 훨씬 다양한 임분구조를 갖는 것으로 추정된다.
| Parameter | a | b | c |
|---|---|---|---|
| Max. | 0.1719 | 2.1910 | 283.5287 |
| Min. | 5.36×10−6 | 0.6252 | 0.7854 |
| Mean | 0.0078 | 1.2766 | 39.7858 |
각 표준지에 대하여 추정한 누적분포와 현실 누적분포를 비교하여 얻은 Kormogrov-Smirnov test(K-S 검정) 결과는 Table 6과 같다. 아까시나무 총 169개의 표준지 중에 164개의 표준지, 즉 전체 표준지의 약 97%가 5%의 유의수준에서 K-S 검정 임계값(critical value)을 통과하여, 단순적률법에 의해 모수 추정된 Weibull 직경분포는 다양한 현실 직경분포 형태를 잘 적합하고 있음을 알 수 있었다. 이 결과는 Lee and Son(2003)이 연구한 천연림인 강원지방소나무와 인공림인 리기다소나무림의 직경분포 추정 K-S 검정 결과와 다소 유사한 값을 가짐을 알 수 있었다.
| Stand | No. of fitted plots/No. of total plots | Fitness index |
|---|---|---|
| Robinia pseudoacacia | 164/169 | 0.9704 |
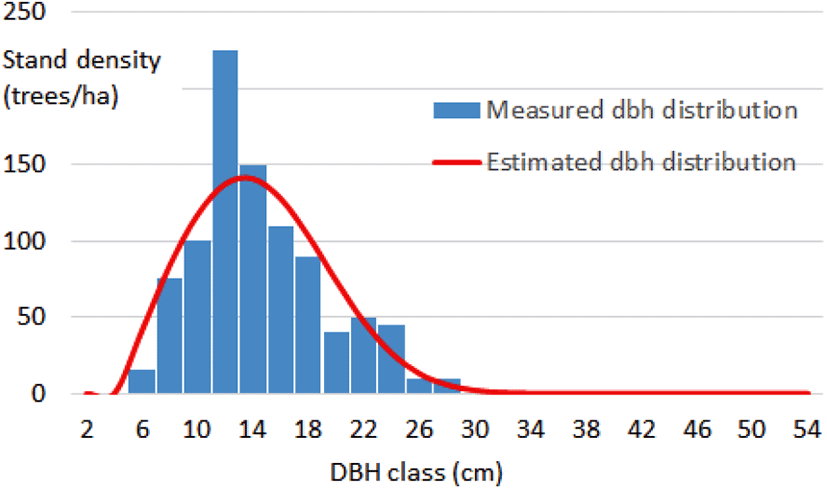
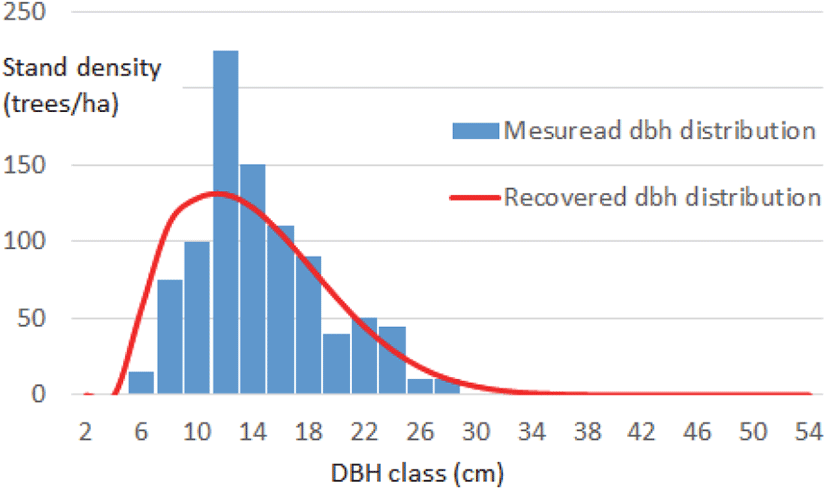
Figure 3은 아까시나무 임분 조사지 중 임의로 선정한 표준지의 직경분포 실측치와 모수추정에 의한 추정치를 비교한 것으로, 실측에 의한 직경분포 중앙값은 14.55 cm이고, 추정에 의한 직경분포 중앙값은 14.50 cm로 나타나, 도식화된 그림뿐만 아니라 수치적으로도 현실임분의 직경분포를 잘 적합시키고 있음을 알 수 있었다.
다음에 설명하게 될 모수 복구에 의한 직경분포 추정과의 차이점은, 본 절에서 분석한 것은 현실 자료 중 직경 표준편차, 평균직경, 최소직경으로 Weibull 함수 모수를 추정하고 적합성을 검증(단순적률법, Simplified method-of-moments)한 것이며, 모수 복구에 의한 방법은 평균직경과 우세목 수고 즉, 우리가 쉽게 구할 수 있는 임분특성으로 최소직경과 직경표준편차를 구하여 Weibull 함수 모수를 추정하고 적합성을 검증한 방법이다.
일반적으로 조사되는 임분특성인 평균직경과 우세목 수고에 의한 최소직경(Dmin), 최대직경 (Dmax) 및 흉고단면적표준편차(BAsd) 추정식을 구한 결과 Table 7과 같았다. Table 7에서 최대직경 및 흉고단면적표준편차 추정식이 최소직경 추정식 보다 설명력이 높은 것으로 나타났다.
| Equations | Fitness index |
|---|---|
| 0.5713 | |
| 0.7287 | |
| 0.7380 |
(Note) Dmin; Minimum stand dbh, Dmax; Maximum stand dbh, BAsd; Standard deviation of stand basal area, ; Mean dbh, HD; Dominant height
각 표준지에 대해 평균직경과 우세목 수고에 근거하여 얻어진 상기 식들을 이용하여 추정한 최소흉고단면적(최소직경에서 얻음) 및 흉고단면적 표준편차 추정치와 평균흉고단면적(평균직경에서 얻음)을 가지고 단순적율법에 의해 흉고단면적 분포에 대한 Weibull 함수의 모수를 추정, 복구하였다. 최종적으로 얻은 흉고직경의 추정분포와 현실분포의 차이를 유의수준 5%에서 검정한 결과, 아까시나무 전체 표준지 중 80.5%가 K-S 검정의 임계값을 통과하는 것으로 나타났다. Figure 4는 임의 선정된 표준지에 대해 실제 경급분포와 모수복구에 의해 추정된 경급분포를 서로 비교ㆍ예시한 것으로, 모수복구에 의한 단계를 거쳐도 현실 직경분포를 잘 적합시키고 있음을 알 수 있었으며, 직경분포의 중앙값이 실측치 14.55 cm와 0.3 cm 정도 차이를 보이는 14.26 cm인 것으로 나타났다.
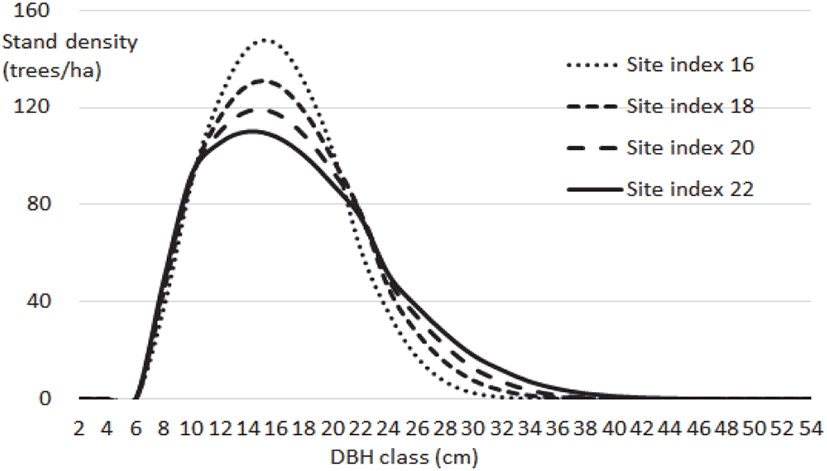
아까시나무 임분의 적지적수 즉, 임지생산력 차이를 확인하기 위하여, 30년생 임분을 기준으로 지위별로 직경급분포를 도식화한 결과는 Figure 5와 같다. Figure 5에 의하면, 지위별로 직경분포는 중경목일 경우, 지위가 높을수록 경급 분포본수가 적어짐을 알 수 있으며, 이렇게 줄어든 입목본수는 결국 직경분포의 정규분포도 상 오른쪽 꼬리 부분으로 이동되어, 이 부분이 점차 확대됨을 알 수 있다. 이는 결국 대경목으로 쓸 용재의 분포가 많아짐을 나타내는 것이라 볼 수 있다.
직경분포 중앙값을 보면, 지위지수 16일 경우 15.98 cm, 지위지수 18은 16.51 cm, 지위지수 20은 16.97 cm, 그리고 지위지수 22는 17.45 cm로 나타나 지위지수가 높아질수록 직경급분포도 오른쪽으로 이동하여, 임분의 평균 직경이 커짐을 알 수 있었다.
따라서 아까시나무 임분을 조성할 시 적지에 맞는 입지를 선정하여야 향후 임분생장의 발달을 도모할 수 있을 것이며, 목재수확 및 바이오매스 증대, 탄소흡수능력 향상 등의 경영 상 능률 극대화를 가져올 수 있을 것이다.
한편 우세목 수고에 절대적인 영향을 지위지수는 인위적 솎아베기에 따라, 지위지수별 직경급 분포변화가 생길 수 있을 것이다. 특히 상층 솎아베기 시는 우세목의 벌목에 따른 지위지수의 변화와 직경급 분포에 많은 변화가 예상되며, 하층 솎아베기 시는 지위지수 자체는 변화가 없으나, 직경분포는 변화가 생길 것으로 보인다. 따라서 이후 후속 연구에서는 솎아베기에 따른 지위지수 및 직경급 분포변화에 대한 시뮬레이션 작업을 수행하고자 한다.
결 론
아까시나무는 우리나라 전국에 분포하며, 고도 또는 지역적 분포에 따라 시기적으로 꽃을 피워 양봉산업에 최상인 꽃샘식물로 자리하고 있으나, 아까시나무 무용론, 여러 차례의 맹아 갱신 등에 따른 황화현상 발생, 사방 또는 연료림으로서의 기능 상실 등에 따라 점차 분포면적이 줄고 있으며, 2014년 연구에 의하면 26,770 ha로 보고되고 있다. 1990년까지의 324천 ha가 조림되었다는 기록과는 10배 이상 감소된 면적이라 할 수 있다.
본 연구에서는 향후 아까시나무 조성 시 적지에 조림하여 낭비가 없는 생육공간에서의 꽃샘식물로 자리매김할 수 있도록 지위지수를 추정하고, 지위지수별 Weibull 직경분포 경향을 알아보고자 하였다. 적지적수는 바로 지위지수와 연계가 되므로 본 연구에서는 아까시나무 지위지수를 추정하기 위해 C-R 모델을 적용하여 지위지수 분류도를 작성하였으며, 그 결과 우리나라에 생육하는 아까시나무의 지위지수 분포는 16~22의 범위에 있었으며, 이는 임분 30년생의 우세목의 수고가 16~22 m 사이에 있는 것이라 해석할 수가 있다.
또한 아까시나무 임분의 지위지수별 직경분포의 변화를 구명한 결과, 분포형태가 지위지수가 높아질수록 그래프가 오른쪽으로 점차 확대됨을 알 수 있는데, 현재의 분석은 임령변화에 따른 자연적인 본수 감소를 중점적으로 분석한 결과이나, 차후 솎아베기에 따른 지위지수 및 직경급 분포 변화에 대한 연구가 필요하다고 본다.
꽃샘식물로서 아까시나무는 아직도 중요한 자원이며, 다른 식물로의 대체를 계획하고 있으나, 이들 수종이 현재 상태를 모두 대체하는 것은 다소 많은 시간이 걸릴 것으로 보인다. 따라서 현재의 생육 및 건강활력도가 다소 떨어지는 아까시나무를 다시 아까시나무로 재조림을 하고자 할 때, 본 연구에서 만든 지위지수 분류표 또는 곡선도를 활용하면 충분히 적지적수를 꾀할 수 있을 것으로 판단된다.
그리고 지위지수별 직경분포 변화를 아까시나무림 경영에 있어 의사결정 자료로 활용한다면, 꿀 생산 뿐만아니라 용재의 확보 측면에서도 효율성을 높일 수 있을 것이라 본다. 한편, 정부 차원에서는 전 세계적인 탄소중립 시대에, 우수한 탄소흡수 능력을 보이는 아까시나무(13.79 tCO2/ha/yr)를 쓸모없이 자리만 차지하는 나무, 목재로서는 가치 없는 나무, 왕성한 번식력으로 다른 나무를 죽이는 나무 등의 오해를 잠재우는 정책과 홍보를 펴나가야 할 시점으로 보인다.