서 론
산사태는 산림지역에서 발생하는 지질재해로, 인간 및 사회기반시설에 심각한 위협이 된다. 특히, 집중호우에 의해 발생하는 천층 산사태(shallow landslide)는 전조현상 없이 순식간에 발생하기 때문에 큰 피해를 야기한다(Choi, 1986; Kim et al., 2013). 국내에서 발생하는 산사태의 주된 원인은 강우이지만, 선행연구에서는 강우인자를 비롯하여 사면경사, 고도, 식생 등 여러 산사태 발생 요인에 대한 많은 연구가 수행되었다(Kim et al., 2005; Yang et al., 2007; Chun et al., 2009; Kim et al., 2011; Oh and Lee, 2014). 하지만 국지적 기후, 지형, 토양, 지질 등 다양한 환경요인에 따라 발생 요인에 대한 분석 결과가 상이한데, 이러한 요소들은 산사태 발생에 복합적으로 기여한다(Sidle et al., 1985; Brardinoni et al., 2002; Sidle and Ochiai, 2006; Imaizumi et al., 2008).
현재까지 산사태 발생 위험성 추정을 목적으로 하는 다양한 방법들이 개발되어 왔으며 대표적으로 경험적 모형, 통계적 모형, 물리 기반 모형으로 구분할 수 있다. 경험적 모형은 주로 위험성 추정을 위한 변수 설정을 위해 전문가의 다양한 의견을 활용한다. 하지만 이러한 의견들은 매우 주관적이며, 지질, 토양, 식생 등 서로 다른 환경 여건을 가진 지역에서 동일한 분석 과정을 진행하기에는 한계점이 있다(Kirschbaum et al., 2016; Hearn and Hart, 2019). 통계적 모형은 데이터를 기반으로 한 접근을 통해 산사태 발생 가능성을 모의하는데, 전술한 두 모형은 모두 과거 및 현재의 산사태 데이터를 이용한 산사태 발생 요인들에 초점을 맞추고 있다(Goetz et al., 2015; Huang and Zhao, 2018). 통계적 모형에서 데이터를 기반으로 한 접근방식이 다른 방식에 비해 정확한 것으로 간주되기도 하지만 산사태 발생 시의 복잡한 물리적 과정들이 간과될 수 있다는 단점이 있다. 반면에 물리 기반 모형은 주로 무한사면 안전공식이나 수문학적 개념을 결합한 사면안정성의 정량화에 주안점을 두고 있는 지질공학적 특성들을 기반으로 하고 있다(Medina et al., 2021). 그러므로 물리 기반 모형의 가장 큰 장점은 산사태 발생 메커니즘을 효율적으로 반영하는 지질학적 과정을 조절하는 물리적 특성들에 기반한 사면안전율의 계산에 있다. 물리 기반 모형은 천층 산사태의 발생 가능성 추정을 위해 빈번하게 활용되고 있으며, 대표적인 모형에는 지질공학적 모델링을 수행하기 위해 Mohr Coulomb의 무한사면 이론을 활용하는 SHALSTAB (Montgomery and Dietrich, 1994)과 TRIGRS(Baum et al., 2008) 등이 있다. 반면 STEP-TRAMM(Fiber Bundle-hexagonal soil columns), SCOOPS 3D 및 R.ROTSTAB 등과 같은 모형은 다른 이론(Stability calculation of grouped cell-columns)을 활용한다(Medina et al., 2021). 또한, 일부 모형(GEOtop-FS, HIRESSS)의 수문학적 메커니즘에서는 지하수의 횡적, 종적 흐름을 고려하기도 하는데(Rigon et al., 2006; Rossi et al., 2013) 대부분 모형(SINMAP, TRIGRS, R.ROTSTAB)들은 하나만을 고려한다(Pack et al., 1998; Baum et al., 2008; Mergili et al., 2014).
산사태 발생 위험성을 평가한 다수의 선행연구에서 급경사지의 산림벌채는 산사태 발생을 촉진시켰는데(Sidle et al., 1985; Montgomery et al., 2000; Glade, 2003; Imaizumi and Sidle, 2012), 이러한 벌채의 영향은 기후, 지질, 지형, 토양 및 식생 등 지역의 환경 여건에 따라 다르게 나타났다(Saito et al., 2017; Lehmann et al., 2019). 다수의 선행연구에서 산림벌채 후 3~10년 사이에 천층 산사태 및 전이형 산사태 발생이 증가한다고 보고되었는데(Bishop and Stevens, 1964; Endo, 1980; Megahan et al., 1978), 이는 벌채목 뿌리의 고사⋅부후와 함께 새로이 침입(식재)한 식생의 뿌리가 충분히 생장하지 못하여 토양 보강 효과가 벌채 이전의 수준보다 낮은 것에 기인한 것으로 지적된 바 있다(Wu et al., 1979; Sidle, 1992). 국내에서는 Wu et al.(1979)의 뿌리 보강 모델을 이용하여 토양 보강 효과를 분석한 연구사례(Lee et al., 1991; Yoo et al., 2001; Kim et al., 2005; Yoo et al., 2010)가 보고되고 있으며, Kim (2013)은 수목의 하중과 뿌리 점착력을 모두 고려한 모형을 이용하여 사면안정성 분석을 실시하였다. 최근 우리나라에서는 목재수확에서 주벌(모두베기)의 비율이 꾸준히 증가하고 있으며(KOSIS, 2022), 2037년까지 30% 이상의 목재자급률을 목표로 하고 있다(KFS, 2018). 또한, 산지전용허가면적은 꾸준히 누적되어 오면서(KOSIS, 2022) 산지 개발로 인한 인접 지역에 재해 발생 위험성은 점차 증가하고 있는 상황이다. 그러나 아직 국내에서는 벌채나 개발 등의 인위적 영향이 산림토양의 물리적 특성 변화에 미치는 영향에 대한 정량적 평가 연구가 충분히 진행되지 못한 상황이다. 이러한 상황에서 물리 기반 모형을 활용한 국지적인 산사태 발생 모의는 산림환경의 변화에 따른 재해 발생의 임계점 및 위험성을 과학적이고 정량적으로 예측·평가하는데 유용한 방법이라고 판단된다.
이러한 배경을 바탕으로 본 연구에서는 2020년 집중호우로 인하여 다수의 산사태가 발생한 제천지역을 중심으로 물리 기반 모형과 무한사면 안정해석을 활용하여 동일 강우 사상에서 벌채지 내 식생 변화에 의한 사면안정성의 정량적 평가를 목적으로 하였다. 이를 위하여 각기 다른 지표유출수의 흐름 기법(Single Flow Direction, Multiple Flow Direction, Infinite Flow Direction)을 가정한 사면안전율 분석을 통해 산사태 발생 가능성을 정량적으로 비교·분석하였다. 또한 산지사면의 안정성에 미치는 뿌리 점착력의 영향을 파악하기 위해 수종별 뿌리 점착력을 차등 적용하고, 벌채지에 대해서는 벌채 후의 경과 연수에 따른 뿌리 점착력의 변화를 고려해 사면안전율 분석을 실시하였다. 이를 통해 벌채 후 식생 환경의 변화에 따른 산사태 발생을 모의하고 사면안정성의 변화 양상을 분석하고자 하였다.
연구방법
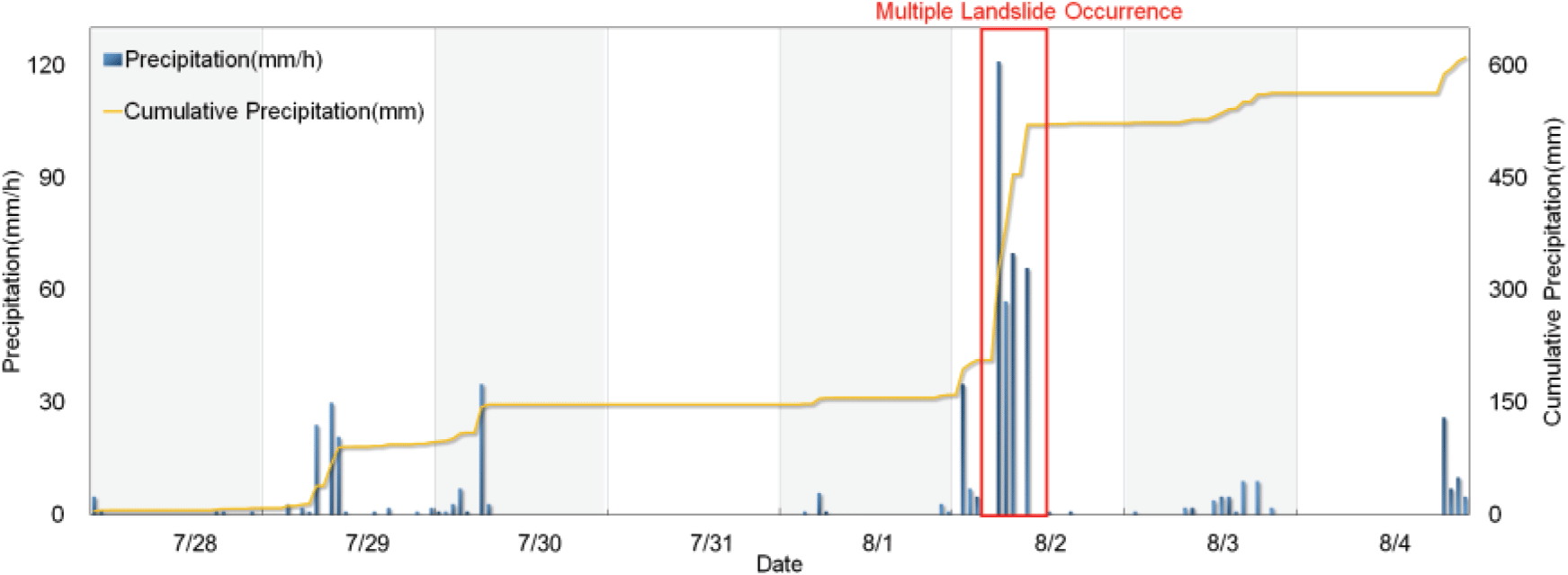
연구지역은 2020년 8월 집중호우로 인해 벌채지를 포함한 산지사면에서 다수의 산사태가 발생한 충청북도 제천시 자원관리센터 일대(37°06'30.16"N, 128°10'21.88"E, 63.8 km2)를 선정하였으며, 사면안전율 분석은 도심지역(평지)을 제외한 41.7 km2를 대상으로 하였다. 연구지역의 표고는 160~505 m, 평균기온은 10.3°C, 연평균강수량은 1,359.3 mm(1991~2020)이다(KMA, 2022). 2020년 8월 집중호우 발생 당시 언론보도 등을 통해 파악한 결과, 충북지역에서 300건 이상의 산사태 피해 신고와 함께 제천지역에서는 120건 및 40 ha 이상의 면적이 산사태 피해를 입은 것으로 보고되고 있다. 연구지역 인근 제천시(삼거리) 기상관측소(http://www.wamis.go.kr/)의 자료에 따르면 대다수의 산사태가 발생한 것으로 추정되는 2020년 8월 2일 이전 5일간 약 160 mm의 선행강우가 있었으며, 2020년 8월 2일 오전 6시경 시간당 최고 121 mm, 일간 363 mm의 집중호우가 발생한 것으로 나타났다(Figure 1).
연구지역의 산사태 발생 전후의 상황은 25 cm급 정사영상을 확보(NGII, 2022)하여 각각의 정사영상별로 4개 이상의 가상의 지상기준점(Ground Control Point, GCP)을 설정하였으며, 항공사진측량 작업 및 성과에 관한 규정(국토지리정보원 고시 제2022-3487호)에 따른 25 cm 해상도 잔차 기준(Root Mean Square Error, RMSE<0.5 m)에 적합하도록 맵핑되었다(x=0.10, y=0.21). 이를 통해 연구지역 내 벌채지 및 산사태 발생원을 파악하였다(Figure 2).
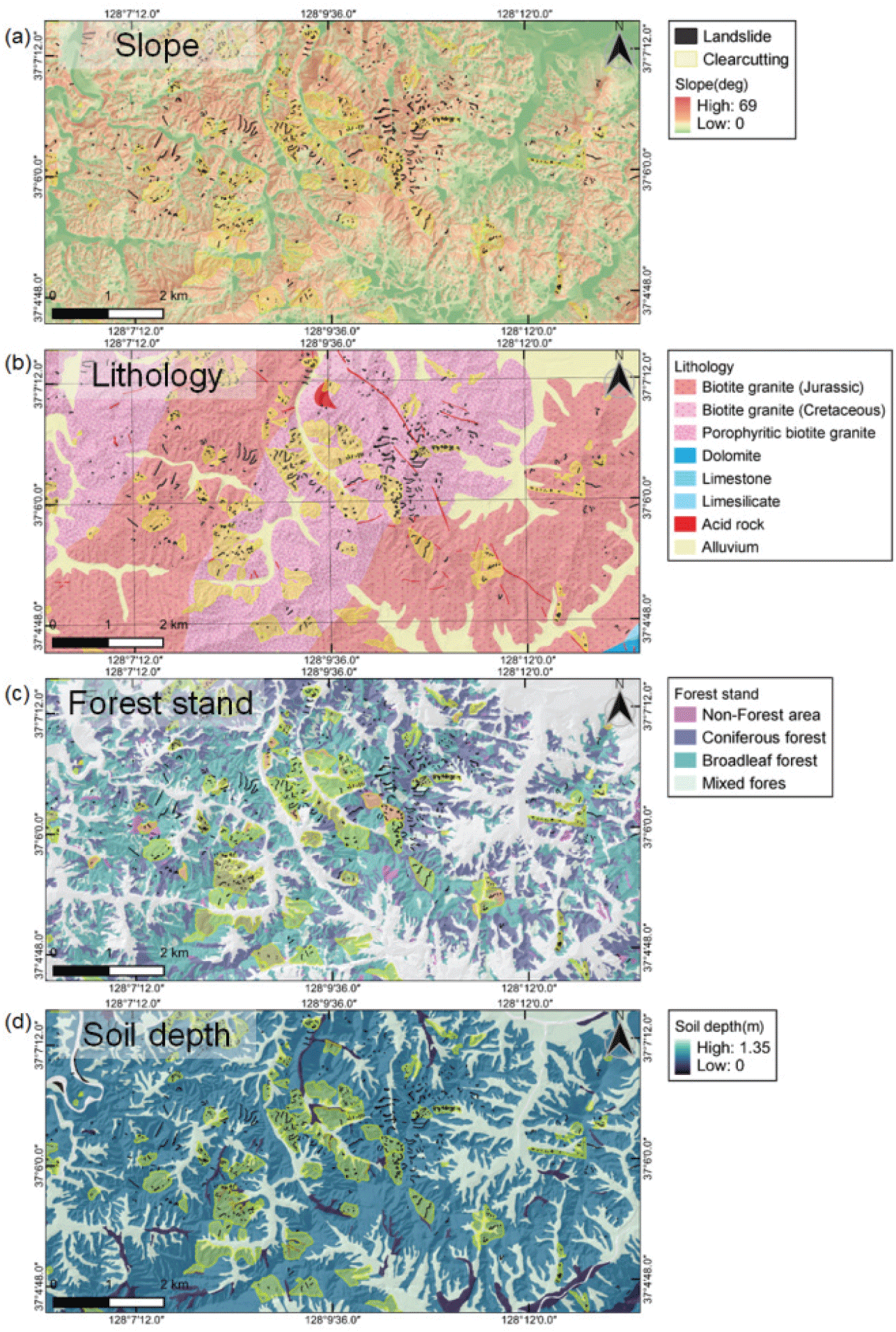
본 연구에서는 연구지역의 사면안전율 분석 및 요인별 산사태 발생 특성 분석을 위해 국토지리정보원에서 제공되는 1:5,000 수치지형도를 활용하여 5 m 간격의 수치표고모형을 제작하였고, 이를 통해 사면 경사를 추출하였다[Figure 3(a)]. 연구지역을 이루고 있는 암석의 공간적 데이터는 한국지질자원연구원 지오빅데이터 오픈플랫폼(https://data.kigam.re.kr/) 1:50,000 지질도를 활용하여 분류하였다[Figure 3(b)]. 또한 연구지역의 수종 및 영급자료[Figure 3(c)]와 토심[Figure 3(d)]은 각각 국가공간정보포털에서 제공하는 산림청의 1:5,000 임상도(http://www.nsdi.go.kr/)와 국립농업과학원의 1:5,000 유효토심도(http://www.nsdi.go.kr/)를 바탕으로 설정하였다. 토양의 물리적 성질 분석을 위한 시료는 연구지역 내(제천시 봉양읍 삼거리 일대, 37°05'37.91"N, 128°08'27.49"E) 벌채지역에서 식생 뿌리가 존재하지 않는 토양을 고려하여 채취하였다. 채취한 시료는 실내에서 습윤단위중량과 건조단위중량을 측정하였다. 또한, 토양투수성측정기(Digital Pereameter, Daiki, Daiki-4056)로 포화상태의 투수성을 측정하였고, 전자동 전단강도 시험기(Shear strength tester, GEOTS, GTS-22-V20)를 이용하여 포화상태의 토양 점착력과 내부마찰각을 분석하여 연구지역에 일괄적으로 적용하였다(Table 1). 이와 함께, 다수의 선행연구에서 보고된 수종별 뿌리 점착력(Table 2)을 사면안전율 분석의 입력변수로 차등 적용하였다.
| Input parameter | Value | Unit |
|---|---|---|
| Dry soil weight | 1,457 | kg/m3 |
| Wet soil weight | 1,898 | kg/m3 |
| Saturated hydraulic conductivity | 0.033 | cm/s |
| Soil cohesion | 3.0 | kPa |
| Internal friction angle | 39.6 | ° |
| Species | Age class | Root cohesion (kPa) | Reference |
|---|---|---|---|
| Pinus densiflora | II | 10.4 | Oh et al.(2011) |
| Pinus koraiensis | V | 15.7 | Kim et al.(2011) |
| Larix kaempferi | II | 10.2 | Oh et al.(2011) |
| Cryptomeria japonica | II | 13.2 | Genet et al.(2008) |
| Quercus mongolica | II | 13.2 | Oh et al.(2011) |
| Alnus japonica | II | 12.7 | Oh et al.(2011) |
| Liriodendron tulipifera | IV | 5.0 | Hales et al.(2009) |
| Populus deltoides | I | 0.5 | Pourmalekshah et al.(2019) |
| Robinia pseudoacacia | I | 15.0 | Wang et al.(2020) |
무한사면 안정해석기법은 지형학적 특성과 토양 특성들이 반영된 모형으로, 사면이 붕괴되는 힘을 받을 때 표층토가 기반암면과 평행하게 움직인다고 가정하고 있으며, 산사태 위험지도 작성 등 사면재해영향 평가를 위하여 광범위하게 사용되고 있다. 본 연구에서 사용한 무한사면 안전율 공식은 다음의 식을 활용하였다(Coduto et al., 2011; Park et al., 2013).
식 1에서, D는 토양의 깊이(m), hw는 토양층 내 지하수면의 수직깊이(m), ρs는 토양의 밀도(kg/m3), ρw는 물의 밀도(kg/m3), β는 사면 경사(°), g는 중력가속도(9.81m/s2), ϕ는 토양의 내부마찰각(°)이다. C′는 Cs + Cr로 표현할 수 있으며, Cs는 토양의 점착력(kPa), Cr은 뿌리 점착력(kPa)이다.
식 1에서 연구지역의 산사태 발생 당시 강우에 의한 지하수위 상승을 고려한 상대습윤지수 산정을 위해 Montgomery et al.(1998)의 식을 활용하였다.
식에서, w는 상대습윤지수, Q는 정상상태 강우량(m/day), a는 상부사면의 기여면적(m2), b는 지표유출수의 흐름방향 단면 폭(m), T는 토양의 투수량 계수(m2/day)이다. 일반적으로 무한사면에서 안전율 공식의 경우 FS=1을 기준으로 1 미만일 경우 불안정, 1 이상일 때 사면을 안정한 것으로 해석한다(Zizioli et al., 2013). 따라서 FS=1이라고 가정하여 식 3을 식 1에 대입하면 다음의 식 4를 통해 사면붕괴를 발생시킬 수 있는 임계강우량(Q)을 유도할 수 있다.
실내실험을 통한 투수계수 산정과 식 4에 의한 계산에 따라 본 연구지역에서 산사태 유발 강우강도 Q는 평균 316 mm/day로 분석되었다. 반면, 산사태 발생 시점으로 추정되는 2020년 8월 2일을 기준으로 연구지역 내 총 363 mm/day의 강우가 발생하였기 때문에 대부분의 토양이 포화되었을 것으로 가정하였다.
상대습윤지수(w)의 범위는 건조상태인 0부터 포화상태인 1까지이며, 1이상인 경우 지표흐름이 발생한다. a/b로 표현되는 비(比) 집수면적(Specific Catchment Area)은 수치표고모형의 해상도에 따라 사면의 방향 및 흐름을 계산하게 된다. 본 연구에서는 5×5 m 격자의 수치표고모형과 SAGA(System for Automates Geoscientific Analyses) 7.8.2 프로그램에서 수문분석을 통해 총 세 가지 흐름 기법(Single Flow Direction Method, SFD; Multiple Flow Direction Method, MFD; Infinite Flow Direction Method, IFD)을 활용한 비 집수면적을 산정하여 사면안전율 분석에 적용하였다(Figure 4).
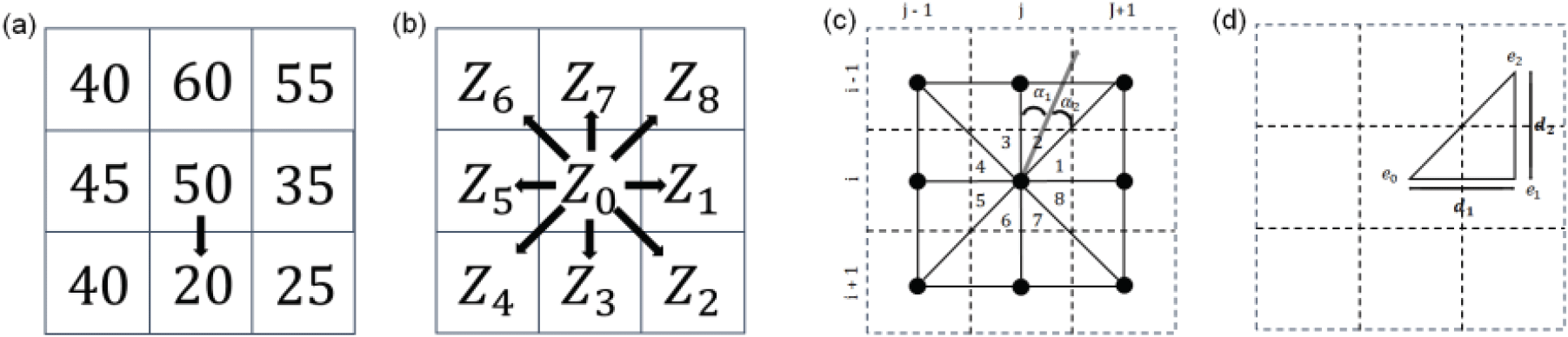
SFD 알고리즘[Figure 4(a)]은 하나의 셀을 중심으로 8개 방향의 셀 사이의 최급하향경사를 갖는 한 개의 셀로 전체 흐름을 할당한다(O’callaghan and Mark, 1984). MFD 알고리즘[Figure 4(b)]의 경우 하나의 셀에 대하여 여러 방향의 흐름을 정의할 수 있다(Quinn et al., 1991). IFD 알고리즘[Figure 4(c), 4(d)]은 0에서 360°까지 방위각을 모두 고려한 후 8개 셀 중 흐름방향과 가까운 두 개 방향으로 지표유출수의 흐름방향을 결정하게 된다(Tarboton, 1997). SFD 알고리즘은 오목형 지형(convergent topography)에서 유동은 비교적 잘 모의하지만, 볼록형 지형(divergent topography)의 유동 모의에는 한계가 있는 것으로 보고되고 있으며, 유체가 여러 방향으로 확산되는 현상을 설명하지 못한다고 알려져 있다. MFD 알고리즘은 반대로 볼록형 지형에서 흐름 분산 효과를 고려하지만, 오목형 지형에서는 흐름의 분산이 과도하게 계산되는 것으로 보고되고 있다(Park and Kim, 2018). IFD 알고리즘의 경우 앞서 언급된 두 가지 알고리즘의 중간 정도 결과를 나타내며, 지형 기복이 크고 고해상도의 수치표고모형 활용 시 이점을 가지지만 완만한 경사에서의 흐름 분석에는 적합하지 않다고 보고되고 있다.
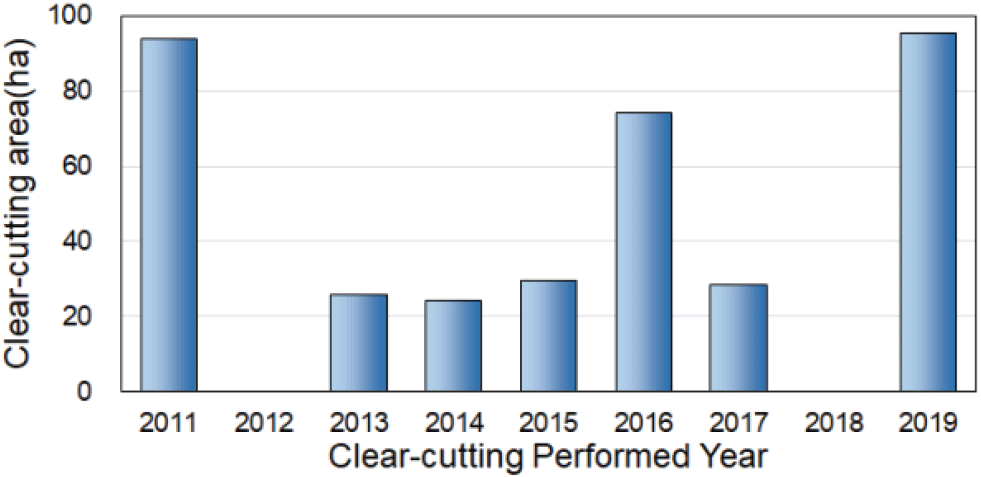
연구지역 내에서 벌채가 수행된 시기를 파악하기 위하여 Google Earth Pro에서 제공하는 영상을 활용하였으며, 이를 통해 제작된 정사영상과 QGIS(Quantum Geographic Information System) 3.28.7 프로그램을 활용하여 해당하는 시기의 벌채 면적을 분석하였다(Figure 5).
벌채 후 경과 연수에 따라 변화된 뿌리 점착력(Cr(t))을 추정하기 위하여 선행연구(Imaizumi et al., 2008; Lehmann et al., 2019)에서 제안된 식을 이용하였으며, 다음의 식과 같다.
식에서, Rmax는 최대 인장강도, t는 시간, CD는 뿌리 고사계수, CG는 생장계수이다. 이때, 본 연구지역 내에 분포하는 모든 수종의 고사계수와 생장계수에 대한 정보는 없으며, 이 연구에서는 벌채 후 뿌리 점착력의 경년변화에 따른 산사태 발생 위험성을 모의하는데 초점을 맞추었으므로 Imazumi et al.(2008)이 제시한 더글러스 전나무(Douglas fir)의 값을 일괄적으로 적용하였다(CD1=0.506, CD2=0.730, CG1=0.952, CG2=19.05, CG3=0.250, CG4=0.05). QGIS 상에서 Table 2를 활용한 수종별 뿌리 점착력 값과 벌채 후의 경과 연수에 따른 뿌리 점착력의 공간 분포는 Figure 6과 같다.
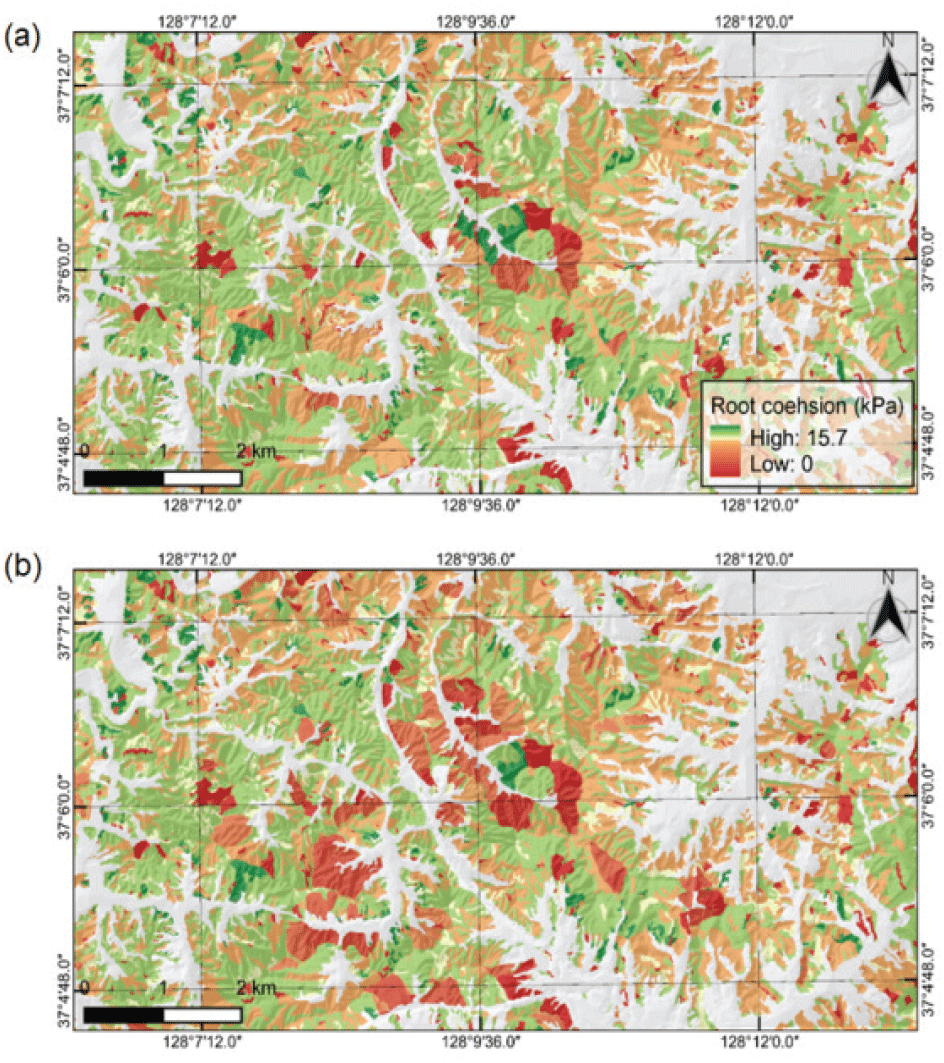
최종적으로 수종별 뿌리 점착력 및 산사태 발생 당시 강우 상황을 기반으로 한 사면안전율 식은 다음과 같이 표현할 수 있다.
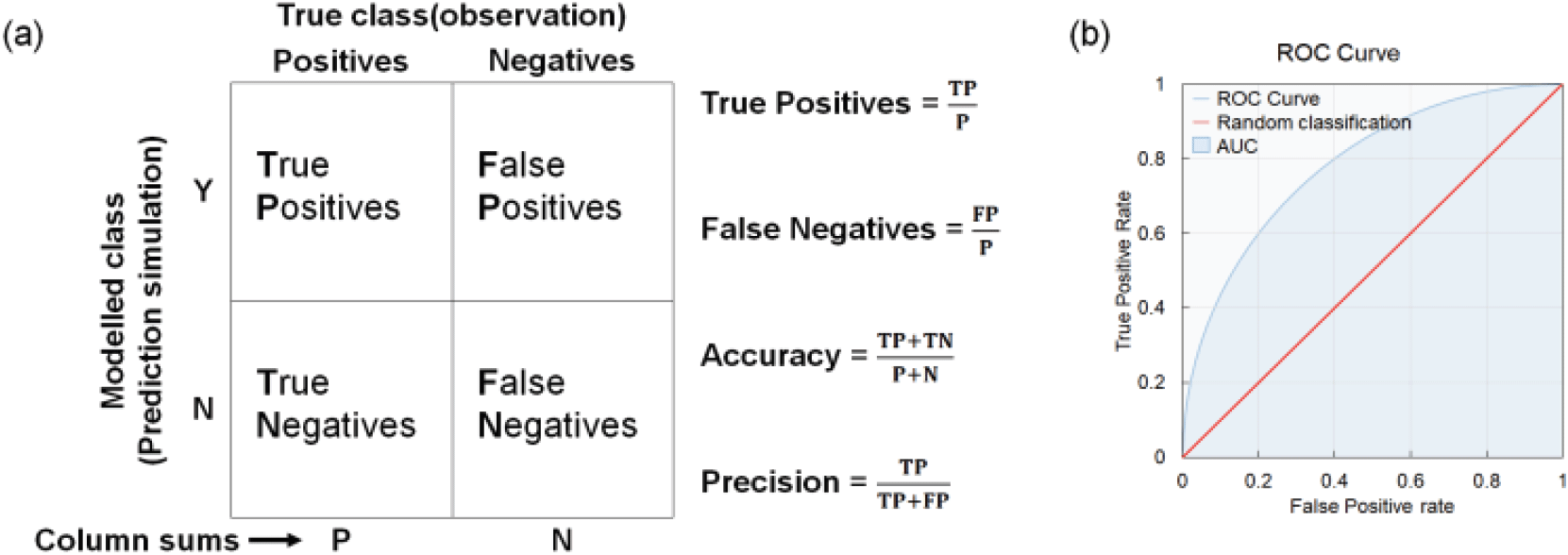
사면안전율 분석 이후 모형의 타당성 검증을 위해 Microsoft Excel 2016 프로그램을 활용하여 AUROC(Area Under the Receiver Operating Characteristics) 분석을 진행하였다. AUROC 분석은 특정 모형의 유용성을 평가하고 모형의 적합성을 판단할 수 있는 정량적 수치로 나타낼 수 있다(Shirzadi et al., 2019). 또한 분석을 통해 나타나는 곡선이 좌측 상단 꼭짓점에 가까울수록 모형의 정확도가 우수한 것으로 판단할 수 있다(Swets, 1988). AUROC 분석은 Figure 7(a)와 같은 Confusion matrix 상에서 4가지 경우로 분류되며, 모형이 불안정으로 예측한 지점에 실제 산사태가 발생한 경우(True Positive, TP), 불안정으로 예측한 지점에 실제 산사태가 발생하지 않은 경우(False Positive, FP), 안정으로 예측한 지점에 실제 산사태가 발생한 경우(True Negative, TN), 안정으로 예측한 지점에 실제 산사태가 발생하지 않은 경우(False Negative, FN)로 나뉜다. 이를 통해 AUROC 분석 이후 모형의 정확도(Accuracy, ACC), 산사태 발생 예측 지점에 실제 발생한 비율(True positive rate, TPR), 산사태 발생 예측 지점에 실제 발생하지 않은 비율(False positive rate, FPR) 및 모형의 적합성을 나타내는 곡선 아래의 면적(Area under the curve, AUC)을 산출해 낼 수 있다[Figure 7(b)]. AUC는 0.5에서 1.0의 범위를 가지며 1.0에 가까울수록 모형의 예측 정확도가 높은 것으로 평가되고 있다(Mehrabi and Moayedi, 2021).
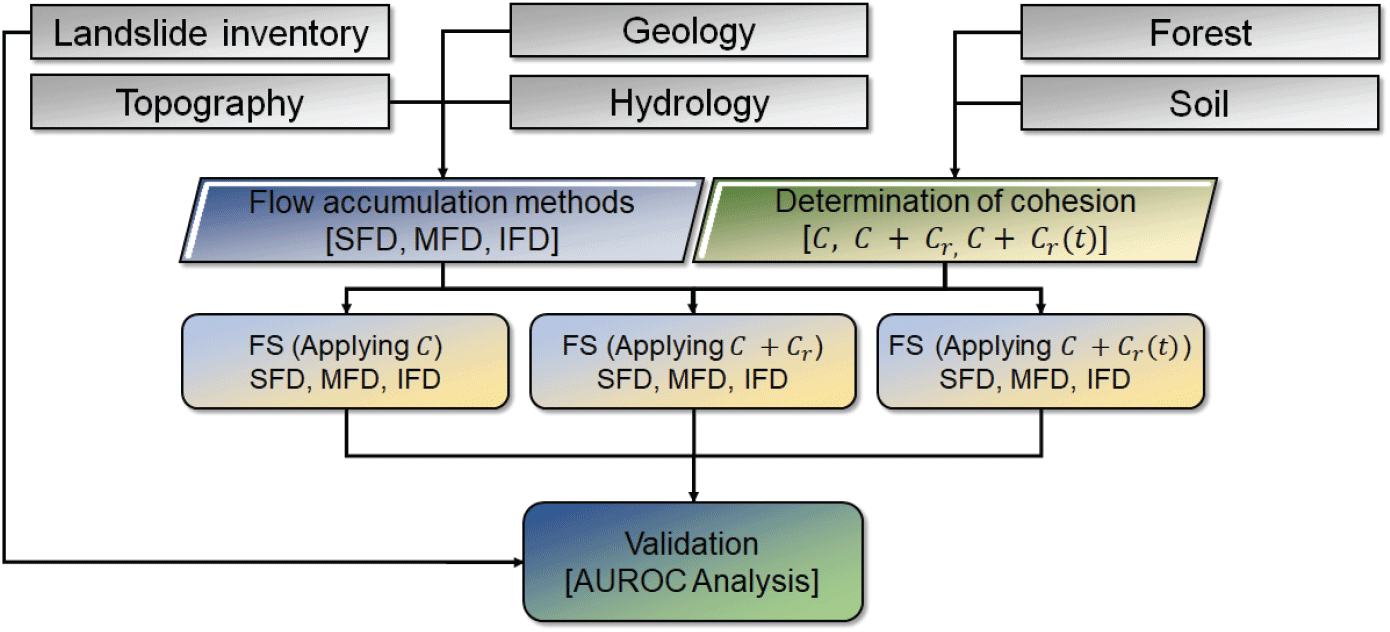
전체적인 연구 진행 과정은 Figure 8 및 Table 3과 같으며, 세 가지 흐름 기법(SFD, MFD, IFD)과 물리 기반 모형에 적용되는 점착력을 세 가지 경우(Cs, Cs + Cr, Cs + Cr(t))로 나누어 QGIS를 활용하여 총 9회에 걸쳐 사면안전율 분석을 실시하였다. 이후 제작된 산사태 인벤토리 맵과 비교하여 AUROC 분석을 통해 모형의 타당성 및 적합성을 검토하였다.
| Group | Flow direction methoda | Soil depth (m) |
Internal friction angle (°) | Soil cohesion (kPa) |
Root cohesion (kPa) |
|---|---|---|---|---|---|
| Result A | 0.0 | ||||
| Result B | SFD, MFD, IFD | 0~1.35 | 39.6 | 3.0 | 11.4 (±3.0)b |
| Result C | 10.8 (±3.5)b |
결 과
연구지역 내 맵핑된 전체 벌채지역은 84개소, 산사태 발생원 830개소로 분석되었으며, 벌채사면에서 479개소(120.9개소/ha), 자연사면에서 351개소(46.8개소/ha)로 벌채사면에서 산사태 발생 빈도가 높은 것으로 분석되었다. 반면, 산사태 규모는 벌채사면에서 총 4.0 ha(82.7 m2/개소), 자연사면에서 총 7.5 ha(213.5 m2/개소)로 자연사면에서 발생한 산사태가 벌채사면에서 발생한 산사태에 비해 큰 규모를 가지는 것으로 분석되었다.
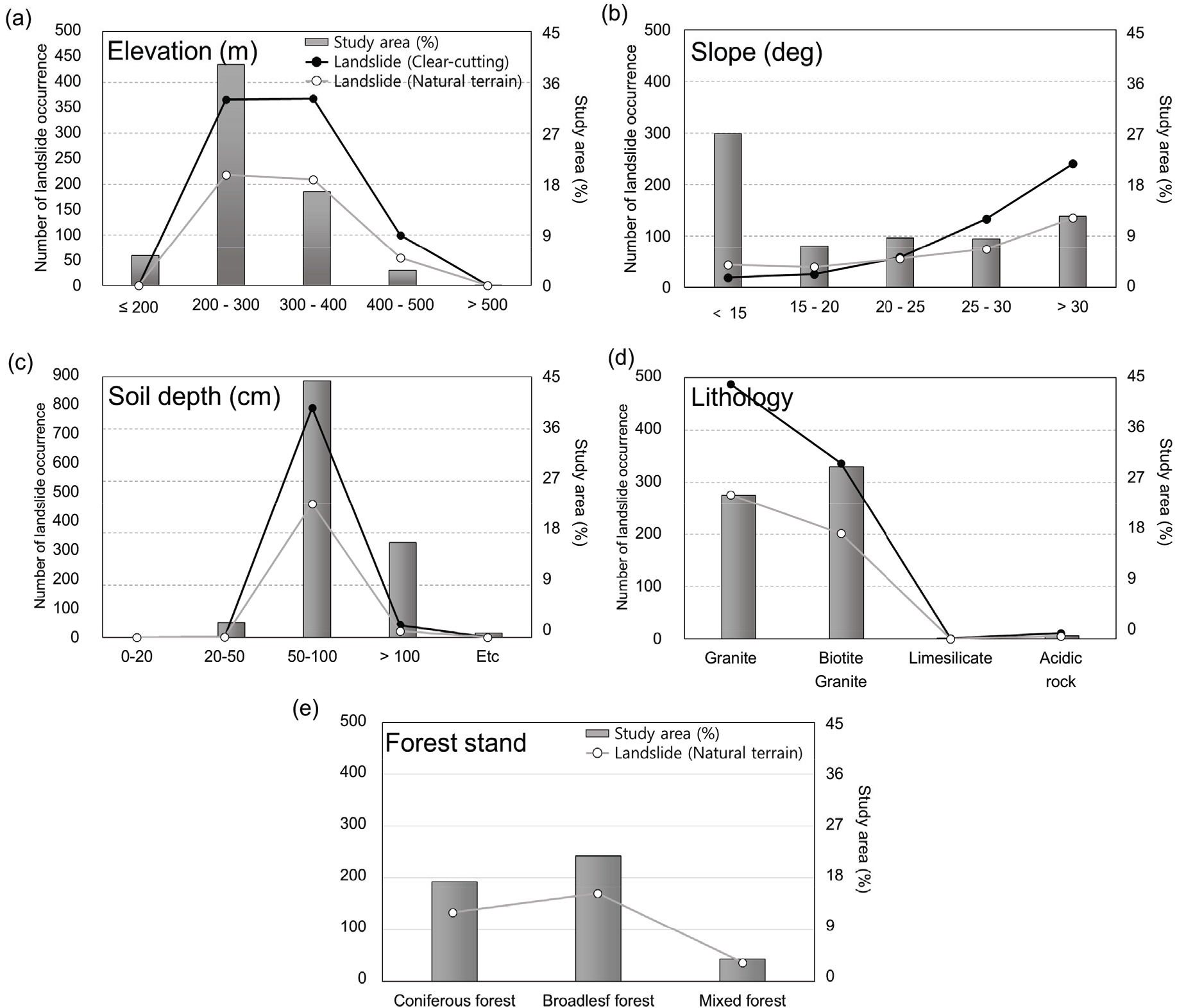
연구지역 고도는 대부분 200~300 m 사이에 분포하고 있지만 대부분의 산사태가 200~400 m 고도에서 발생하였으며[Figure 9(a)], 경사는 15° 이하의 지형이 대부분이지만 30° 이상의 급경사지에서 대부분의 산사태가 발생한 것으로 분석되었다[Figure 9(b)]. 연구지역 토심은 50~100 cm로 비교적 얕은 토심 형태를 보이며 50~100 cm 구간에서 산사태 발생 빈도 또한 높은 것으로 분석되었다[Figure 9(c)]. 연구지역을 이루고 있는 암석은 거정질 흑운모 반상화강암이 대부분인 화강암 지대이며(Woo and Park, 2004), 자연사면과 벌채사면 모두 반상 화강암 및 흑운모 화강암과 같은 화강암 지대에서 다수의 산사태가 발생하였다[Figure 9(d)]. 연구지역 임상은 침엽수림 35%, 활엽수림 44%, 혼효림 8%로 구성되어있으며, 산사태 발생은 침엽수림 128개소, 활엽수림 165개소, 혼효림 30개소로 분석되었다[Figure 9(e)].
사면안전율 분석은 현장 조사 및 실내 실험을 통한 수리전도도, 내부마찰각, 점착력 등 물리적 특성을 비롯하여 항공영상 및 지질도, 임상도 등과 함께 전술한 실제 산사태 발생 당시 강우강도를 기반으로 도출된 결과를 활용하여 AUROC 분석을 실시하였다. 사면안전율 분석은 산사태 피해지역이 아닌 발생원의 분석 및 시각화를 목표로 하기 때문에 도심지역 및 주거지역은 제외하였다. 각각 세 가지 흐름 기법을 활용한 비 집수면적을 산정하여 사면안전율 분석에 적용하였으며, Acharya et al.(2006)이 제안한 사면안전율 분류 기법을 참고하여 지리정보시스템을 통해 시각화 및 정량적 수치 비교를 실시한 결과는 다음과 같다.
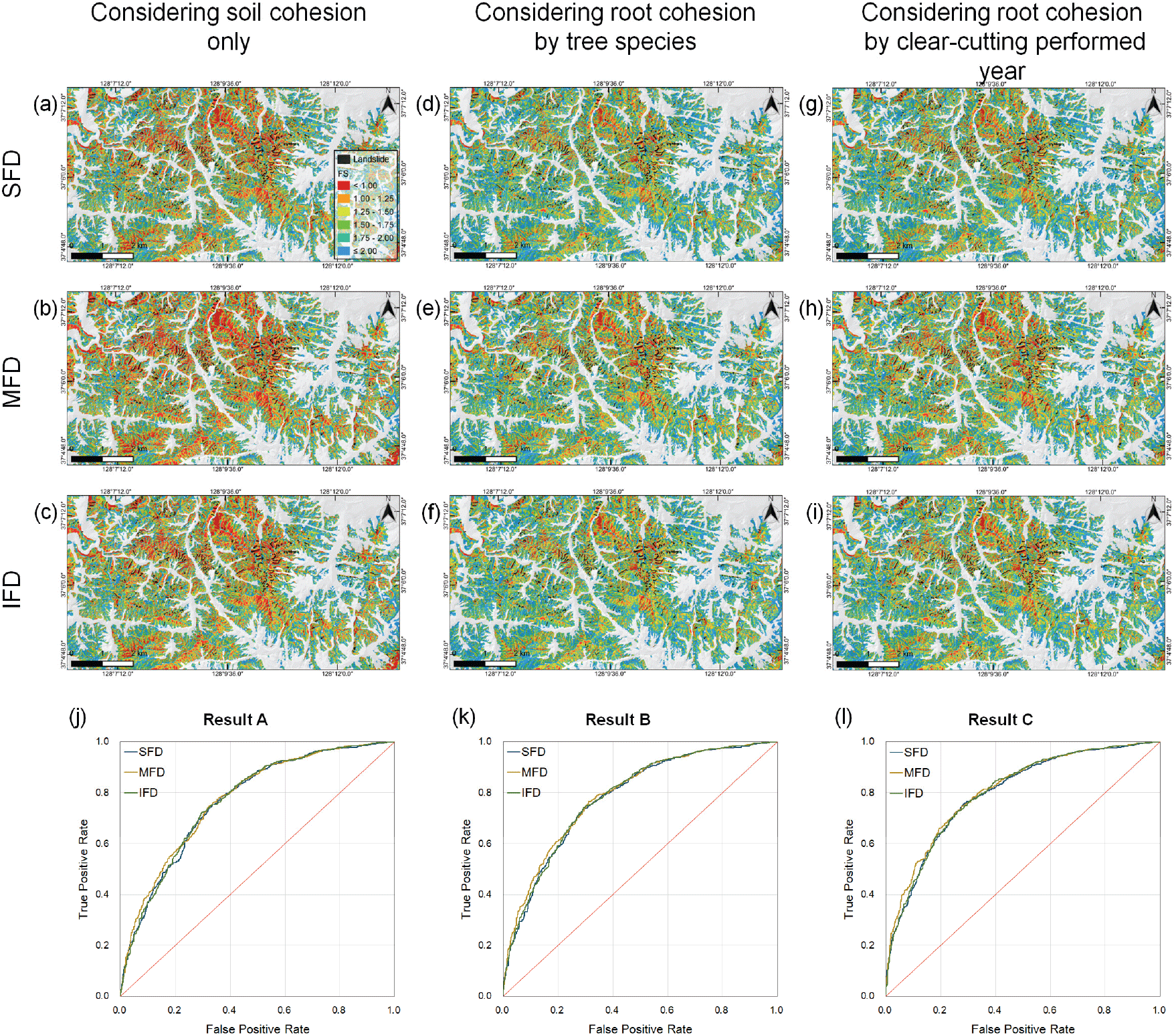
Figure 10(a), Figure 10(b), Figure 10(c)는 연구지역에 포화 토양의 점착력(3kPa)만을 적용하여 계산된 사면안전율이다. 분석 결과는 순서대로 SFD 알고리즘[Figure 10(a)], MFD 알고리즘[Figure 10(b)], IFD 알고리즘[Figure 10(c)]을 활용한 결과이며, Figure 10(j)는 분석된 결과를 사전에 제작된 산사태 인벤토리 맵을 기반으로 AUROC 분석을 진행한 결과이다.
사면안전율 분석 이후 FS 분류에 따른 구간별 셀의 개수를 분석한 결과(Table 4) 사면 불안정으로 분석된 셀은 SFD 알고리즘에서 204,423개, MFD 알고리즘에서 265,793개, IFD 알고리즘에서 204,353개로 분석되었으며, 안정 사면으로 분류된 셀은 SFD 알고리즘에서, 1,418,628개, MFD 알고리즘에서 1,357,258개, IFD 알고리즘에서 1,418,698개로 분석되었다. 전체 분석지역을 대상으로 각 흐름 기법별 불안정 셀의 비율은 SFD 알고리즘과 IFD 알고리즘 모두 12.6%로 분석되었으나, MFD 기법에서 16.4%로 다른 기법에 비해 약 3.8%p 높은 것으로 분석되었다
| Classification | < 1.00 | 1.00~1.25 | 1.25~1.50 | 1.50~1.75 | 1.75~2.00 | ≥ 2.00 | Note | |
|---|---|---|---|---|---|---|---|---|
| Result A | SFD | 204,423 | 290,968 | 289,994 | 220,251 | 153,980 | 463,435 | Figure 10a |
| MFD | 265,793 | 333,170 | 293,653 | 205,579 | 136,816 | 388,040 | Figure 10b | |
| IFD | 204,353 | 308,729 | 303,262 | 225,944 | 154,111 | 426,652 | Figure 10c | |
| Result B | SFD | 79,688 | 207,724 | 289,023 | 260,152 | 192,661 | 582,850 | Figure 10d |
| MFD | 103,482 | 258,169 | 316,546 | 257,649 | 178,035 | 498,217 | Figure 10e | |
| IFD | 74,790 | 217,683 | 304,932 | 270,043 | 196,045 | 548,605 | Figure 10f | |
| Result C | SFD | 87,741 | 215,987 | 288,134 | 255,975 | 189,390 | 574,871 | Figure 10g |
| MFD | 114,687 | 265,730 | 313,116 | 252,559 | 174,528 | 491,478 | Figure 10h | |
| IFD | 83,006 | 226,763 | 303,701 | 265,347 | 192,525 | 540,756 | Figure 10i | |
사면안전율 분석 이후 실제 발생한 산사태를 기반으로 제작된 인벤토리 맵과 비교하여 AUROC 분석을 진행한 결과(Table 5), 실제 발생한 산사태와 일치하는 비율인 TPR(SFD: 0.39, MFD: 0.49, IFD: 0.38)과 모형의 적합성을 나타내는 AUC 값(SFD: 0.77, MFD: 0.78, IFD: 0.77)은 세 가지 흐름 기법 모두 양호한 수준인 것으로 판단되나, 실제 발생한 산사태와 일치하지 않는 비율인 FPR(SFD: 0.11, MFD: 0.15, IFD: 0.11)도 비교적 높은 것으로 나타났다.
일반적인 산림지역에서 사면안전율 분석을 위해서는 토양의 점착력뿐만 아니라 산림 내 존재하는 수목 근계에 의한 뿌리 점착력을 고려하여야 한다. Figure 10(d), Figure 10(e), Figure 10(f)는 1:5,000 임상도를 기반으로 연구지역 내 수종별 점착력을 차등 적용하여 사면안전율을 분석한 결과를 나타낸 그림이다.
사면안전율 분류에 따른 셀 개수를 파악한 결과(Table 4)는 앞선 결과에 비해 불안정 셀의 개수(SFD: 79,688, MFD: 103,482, IFD: 74,790)가 상당히 감소한 것으로 나타났으며, 이에 따라 안정 셀의 개수(SFD: 1,532,410, MFD: 1,508,616, IFD: 1,537,308)는 증가한 것으로 분석되었으며, 불안정 셀의 비율은 SFD 알고리즘에서 4.9%, MFD 알고리즘에서 6.4%, IFD 알고리즘에서 4.6%로 이전 결과와 같이 MFD 알고리즘에서 가장 많은 불안정 셀을 계산하는 것으로 나타났다.
AUROC 분석을 통한 수치 비교 결과(Table 5, Figure 10k) 실제 발생한 산사태와 모형의 일치 비율인 TPR(SFD: 0.21, MFD: 0.28, IFD: 0.20)은 이전 결과에 비교하여 감소하였으나, FPR(SFD: 0.03, MFD: 0.05, IFD: 0.03)이 상당히 감소하여 결과적으로 모형의 적합성인 AUC 값(SFD: 0.78, MFD: 0.79, IFD: 0.79) 또한 소폭 상승한 것으로 나타났다.
산림벌채 이후 사면에서 수목의 근계에 의한 토양 보강 효과는 점차 감소하며, 이후 새로운 식생의 활착 및 도입을 통해 수목의 뿌리가 생장하며 전체적인 토양 보강 효과는 증가한다. 연구지역은 산사태 발생 전 약 10여 년간 총 84개소의 크고 작은 산림벌채로 인하여 식생 및 산림 생태계 변화가 진행되었다. 이와 같은 상황에 고강도의 강우가 발생할 경우 산사태 발생 예측을 위한 사면안전율 분석의 정확성을 높이기 위해서는 벌채에 따른 수목의 뿌리 점착력 변화를 고려하여야 한다. Figure 10(g), Figure 10(h), Figure 10(i)는 연구지역에 수종별 뿌리 점착력을 적용한 Result B에 더불어 벌채 경과 연수에 따른 수종별 뿌리 점착력의 변화를 고려하여 적용한 사면안전율 분석 결과이다.
사면안전율 분석결과, 불안정 셀의 개수(Table 4)는 SFD 알고리즘에서 87,741개, MFD 알고리즘에서 114,687개, IFD 알고리즘에서 83,006개로 앞서 분석한 Result B와 비교하여 소폭 증가한 것으로 나타났다. 안정 셀의 개수는 SFD 알고리즘에서 1,524,357개, MFD 알고리즘에서 1,497,411개, IFD 알고리즘에서 1,529,092개로 분석되었으며, 불안정 셀 비율은 SFD 알고리즘에서 5.4%, MFD 알고리즘에서 7.1%, IFD 알고리즘에서 5.1%로 Result A, B와 같이 MFD 알고리즘에서 불안정 셀 비율이 가장 높은 것으로 계산되었다(Table 4).
벌채 후의 경과 연수별 뿌리 점착력의 변화를 고려하여 사면안전율을 계산한 결과를 기반으로 AUROC 분석을 진행한 결과(Table 5) 실제 발생한 산사태와 모의결과가 일치하는 비율인 TPR은 SFD 알고리즘에서 0.26, MFD 알고리즘에서 0.34, IFD 알고리즘에서 0.26으로 수종별 점착력만을 고려한 Result B에 비해서 상당히 증가하였으며, FPR은 변동이 없었다. 결과적으로 모형의 적합성인 AUC는 SFD 알고리즘에서, 0.80, MFD 알고리즘에서 0.81, IFD 알고리즘에서 0.80으로 Result A, Result B와 비교하여 가장 높은 적합성으로 분석되었다(Figure 10l).
토양 점착력만을 고려한 사면안전율 분석의 경우 수종별 점착력 및 벌채에 따른 점착력 변화를 고려한 분석 결과에 비하여 사면안전율이 1 미만인 불안정 사면의 셀 개수가 2.3~2.7배 많게 나타났고, FS가 1 이상인 안정 사면으로 분류되는 셀의 개수는 약 0.9배로 낮은 것으로 분석되었다. 또한 벌채에 따른 뿌리 점착력의 변화를 고려한 경우 단순 수종별 점착력을 고려해 분석한 결과보다 불안정으로 분석되는 셀의 개수는 약 1.1배 높은 것으로 분석되었다.
흐름 기법에 따른 사면안전율 분석에서 SFD 기법을 활용하였을 경우 MFD 기법에 비해 불안정 셀 개수는 0.8배로 낮았으며, IFD 기법과 비교하였을 때 약 1.1배로 비교적 높은 것으로 분석되었다. 결과적으로 MFD 기법을 활용한 사면안전율 분석에서 다른 기법에 비해 불안정 셀의 개수가 약 1.3~1.4배 높았고, 안정 셀의 개수는 0.96~0.98배로 비교적 낮은 것으로 분석되었다.
고 찰
전체 산사태 발생원 830개소 중 벌채지에서 479개소(58%), 자연사면에서 351개소(42%) 산사태가 발생하였으며 벌채지에서 자연사면과 비교해 약 1.4배 높은 빈도의 산사태 발생이 관측되었다. 반면 연구지역 내 산사태 발생 면적은 자연사면에서 7.5 ha, 벌채지에서 4.0 ha로 자연사면에서 약 1.9배 높은 것으로 분석되었으며, 벌채지 및 자연사면에서 산사태 규모는 자연사면(213.5 m2/개소)이 벌채사면(82.7 m2/개소)보다 평균 2.6배 높은 것으로 분석되었다. 선행연구에 따르면 토양 내 뿌리의 밀도가 높은 경우 뿌리-토양 간 전단이 주변 토양의 전단보다 크기 때문에 수목 전도 시에 토양이 뿌리와 결합하여 블록상으로 분리되는 경향이 있는 것으로 보고된 바 있다(Giadrossich et al., 2013; Vergani et al., 2017). 따라서 비교적 살아있는 뿌리의 밀도가 높은 자연사면에서 산사태가 발생할 경우에는 다수의 수목이 전도되면서 블록상 토양층 붕괴의 발생 및 지표유출수 유입에 따른 확대로 인해 산사태 규모가 증가할 수 있다고 추측된다. 이러한 결과는 자연사면의 사면안정성 및 산사태 발생(피해) 규모 분석에 있어 입목의 영향도 고려할 필요가 있음을 시사한다.
연구지역 요인별 산사태 발생 특성을 분석한 결과 고도, 토심, 암석, 임상 요인의 경우 분류별로 넓은 면적을 차지하는 지역에서 다수의 산사태가 발생하였다. 연구지역 토심의 경우 50~100 cm 토심 지역이 69%로 대부분을 형성하고 있다[Figure 9(c)]. 국내 요인별 산사태 발생 특성과 관련된 선행연구에 따르면 연구지역 토심과 같은 형태의 얕은 토심으로 형성된 지역에서 짧은 시간 높은 강도의 강우 발생 시 토양은 빠르게 포화되며 침투능이 저하되어 산사태 발생 확률이 증가하는 것으로 판단된다(Campbell, 1975; Kim et al., 2005; Chun et al., 2009). 경사는 증가할수록(30°) 다수의 산사태가 발생하였으며, 국내 선행연구들의 결과와 비슷한 양상을 보였다(Yang et al., 2007; Kim et al., 2011; Oh and Lee, 2014). 연구지역 고도의 경우 200~300 m의 지역이 61%로 대부분이었으며[Figure 9(a)], 고도별 산사태 발생 양상 및 임상에 따른 산사태 취약성을 보고한 여러 연구들과는 상이한 결과가 나타났다(Chun et al., 2009; Kim et al., 2011; Oh and Lee, 2014).
사면안전율 분석은 연구지역에 토양 점착력만 적용한 경우, 수종별 뿌리 점착력을 고려한 경우, 벌채 후의 경과 연수에 따른 뿌리 점착력의 변화를 고려한 경우 세 가지로 나뉘며, 각각의 분석에서 지표유출수 흐름 기법을 세 가지로 나누어 총 9회의 사면안전율 분석을 진행하였다(Table 3). 흐름 기법별 사면안전율 분석에서 MFD 알고리즘의 경우 다른 지표유출수 흐름 기법을 적용하였을 때보다 TPR은 26~40% 높았으며, FPR은 36~67% 더 높게 분석되었다. AUC는 약 0.0~1.3% 높은 것으로 분석되어 모형의 적합성은 다른 흐름 기법과 비교하여 향상된 것으로 판단되나 높은 수준은 아니었다. 반면, MFD 알고리즘은 다른 두 알고리즘과 비교하여 불안정 셀 개수는 약 30~38% 더 높은 것으로 계산되었으며, 안정 셀의 경우 2~4% 더 낮은 것으로 분석되었다. 결과적으로 MFD, SFD IFD 알고리즘 순으로 불안정 셀의 개수가 높은 것으로 분석되었다. 이와 같은 결과는 MFD 알고리즘이 기여 면적 내 모든 초과강우가 직접유출 생성에 기여하는 SFD 알고리즘과 달리 흐름방향을 여러 방향으로 모의할 수 있는 반면(Park and Kim, 2018), 지표유출수가 수렴하는 형태의 지형에서는 흐름이 과도하게 측정되는 것에 기인한 결과로 판단된다(Park et al., 2009). IFD 알고리즘의 경우 흐름방향을 8개 방향으로 고려하는 SFD, MFD 흐름 기법과 비교하여 물리적 특성과 이론적 분산효과의 차이로 급경사지역 흐름이 과도하게 분산된 것으로 판단된다(Lee et al., 2012).
벌채 후 식생 변화를 고려한 점착력을 이용한 분석에서는 토양 점착력만을 적용한 Result A에서 Result B, Result C와 비교하여 불안정 셀 개수가 약 2.3~2.7배로 상당히 높은 것으로 분석되어 실제 산사태 발생 결과와는 다르게 불안정 면적이 과도하게 큰 것으로 나타났다. 이는 수목 뿌리에 의한 사면안정 보강 효과를 방증하는 결과로도 해석할 수 있다. 불안정 셀 개수는 수종별 점착력을 고려한 Result B에서 약 61~63% 대폭 감소하였으며, 벌채 영향에 따라 뿌리 점착력을 재분배하여 계산된 Result C에서 다시 약 10~11% 증가한 것으로 분석되었다. 이는 뿌리 점착력의 변화와 사면안전율의 상관관계를 다룬 국외의 선행연구(Imaizumi et al., 2008; Saito et al., 2017; Lehmann et al., 2019)에서 보고된 바와 같이 벌채로 인한 뿌리 점착력의 감소가 실제 연구지역 사면안전율의 감소로 작용되었기 때문으로 판단된다.
AUROC 분석 결과 과도한 불안정 면적을 보이는 Result A에서 실제 산사태 발생 위치와 일치하는 비율은 높게 나타났으나, 일치하지 않는 비율 또한 비교적 높은 것으로 판단된다. Result A와 수종별 점착력을 고려한 Result B를 비교하였을 때 TPR은 43~47% 감소하였지만, FPR 또한 67~73% 감소하였다. 추가적으로 벌채 영향에 따른 뿌리 점착력의 변화를 고려한 Result C의 경우 단순 수종별 점착력을 고려한 Result B와 비교하여 TPR은 21~30% 증가하였으며, FPR은 변화하지 않았다. 결과적으로 토양의 점착력만을 고려한 경우(Result A) 보다 수종별 벌채에 따른 뿌리 점착력 변화를 고려하여 사면안전율을 분석한 경우(Result C) 모형의 적합성을 나타내는 AUC는 3.85~3.90% 향상되었으며, 수종별 점착력을 고려한 경우(Result B) 보다 1.3~2.6% 향상되었다. Result A, Result B, Result C의 값을 비교해 보았을 때 산사태가 발생할 것으로 예측되는 지역에 실제 산사태가 발생한 비율(TPR)이 가장 높은 Result A가 정확하다고 판단될 수 있다. 그러나 Result A의 경우에는 실제 물리 기반 수치모의를 통해 산사태 취약지역을 파악하거나 예방사업을 계획할 시 과도하게 큰 면적이 산사태 위험지역으로 분석될 우려가 있다. 따라서, 이러한 결과를 종합하면 벌채 후의 수종별 뿌리 점착력의 경년변화를 고려한 Result C가 산사태 발생 가능성 모의 및 평가에 있어서는 가장 적정하고 유의미한 결과라고 판단된다.
한편, 본 연구에서는 토양의 물리적 특성(i.e., 내부마찰각=39.6°, 포화상태 토양 점착력=3kPa)과 함께 수목 뿌리의 고사계수와 생장계수를 일괄 적용하였다는 한계는 있다. 그러나 분석결과를 통해 산사태 발생 위험 모의에 있어 수목 뿌리의 점착력과 벌채에 따른 그 변화가 산사태 예측의 정확성에 미치는 영향에 대해서 정량적으로 확인할 수 있었다. 앞으로 지질, 지형, 임상 등의 분포를 충분히 고려하여 토양의 물리적 특성의 면밀한 분석과 분류, 그리고 공간분포지도 제작이 이루어진다면 사면안전율 분석의 정확성을 향상시킬 수 있을 것으로 판단된다.
결 론
본 연구는 2020년 8월의 집중호우로 인해 많은 산사태가 발생한 제천지역을 대상으로 산사태 인벤토리 맵을 제작하여 연구지역의 요인별 산사태 발생 특성을 분석하고, 지표유출수 흐름 기법 및 임상에 따른 토양 내 점착력 변화를 반영하여 사면안전율 분석을 실시하였다. 그 결과, 연구지역 내 전체 산사태 발생원 중 벌채사면에서 자연사면보다 약 1.4배 높은 산사태 발생 빈도를 보였으며, 지질, 임상, 토심 등 연구지역의 내적요인들을 고려하면 단시간 고강도의 강우 발생 시 산사태 발생 민감성이 높은 지역으로 판단되었다.
연구지역 내 벌채지 및 실제 산사태가 발생한 지점의 인벤토리 맵을 활용하여 사면안전율 분석 이후 AUROC 분석을 통해 모형의 타당성을 검증하였다. 그 결과, 활용된 세 가지 흐름 기법(SFD, MFD, IFD) 중 MFD 알고리즘을 활용한 경우는 다른 흐름 기법과 비교하여 모형의 적합성이 최대 1.3% 소폭 향상되었다. 토양 내 점착력 분류에 따른 사면안전율 분석(토양의 점착력만을 고려한 경우, 수종별 뿌리 점착력을 고려한 경우, 벌채 영향에 따른 뿌리 점착력 변화를 고려한 경우)에서는 벌채 후의 경과 연수를 기반으로 수종별 뿌리 점착력 변화를 고려하여 사면안전율 분석을 실시하였을 때 모형의 적합성은 약 1.27~3.90% 향상되었다.
본 연구에서는 수확벌채가 시행된 지역에서 벌채 후의 경과 연수에 따른 토양 보강 효과를 분류하여 사면안전율을 분석한 결과, 과도한 사면불안정 값이 개선되는 것으로 나타났다. 또한, 고해상도 항공영상을 활용한 산사태 인벤토리 맵의 제작과 분석을 통해 모형의 적합성이 향상될 수 있음을 확인하였다. 산사태 발생 우려가 있는 지역에서는 효과적인 산사태 발생 예측을 위해 수종별 뿌리 점착력과 벌채 등에 따른 그 변화를 고려한 수치모의를 통하여 정량적인 산사태 발생 위험성 분석이 필요하다고 판단된다. 향후 현장조사 및 실내실험에 기초하여 지질, 지형 및 임상 등 입력변수의 세분화가 이루어진다면 모형의 정확성을 향상시킬 수 있을 것으로 판단된다.