서 론
수목의 뿌리는 토양 입자를 결속하고 지상부를 지탱하는 역할을 하며, 생장에 필요한 수분과 양분을 흡수한다(Genet et al., 2008; Buza and Divós, 2016; Cohen and Schwarz, 2017; Alani and Lantini, 2020). 특히, 산림공학 측면에서 뿌리는 토양의 점착력을 높이고 마찰저항을 증가시켜 산지 비탈면의 구조적 안정에 크게 기여한다(Buza and Divós, 2016; Cohen and Schwarz, 2017; Yamase et al., 2018). 이러한 뿌리에 의한 토양 보강 효과는 뿌리의 물리적 특성과 공간적 분포에 의해 영향을 받는다(Cohen and Schwarz, 2017; Yamase et al., 2018). 따라서 수목 뿌리의 크기와 위치를 정확하게 파악하는 것은 수목 뿌리에 의한 비탈면 안정 및 산사태 예방 효과를 정량적으로 추정하는 데 매우 중요하다.
수목 뿌리의 형태적 특성과 공간적 분포는 발굴(excavation)이나 굴취(digging) 등을 통해 현장에서 직접 조사하거나(Krainyukov and Lyaksa, 2016; Alani and Lantini, 2020) 조사기기를 사용하여 비파괴적 방법으로 조사한다(Lantini et al., 2018; Tosti et al., 2018). 직접 조사방법은 직관적이고 정확한 정보를 취득할 수 있지만, 조사에 많은 시간과 비용이 요구되고, 현장조사 과정에서 수목 뿌리가 훼손되거나 손상되기도 한다는 단점이 있다(Hruska et al., 1999; Yamase et al., 2018; Alani and Lantini, 2020). 이러한 이유로 최근에는 수목에 대한 피해가 상대적으로 적은 비파괴 조사법(non-destructive test)이 이용되고 있다. 비파괴 조사법은 물체의 전자기 특성을 이용하여 대상물에 직접적인 손상을 일으키지 않고 물체의 공간적 분포나 특성을 조사하는 방법이다(Hruska et al., 1999; Jol, 2009; Buza and Göncz, 2015; Buza and Divós, 2016; Tosti et al., 2018).
이러한 비파괴 조사법을 이용한 뿌리 조사는 근관찰관(rhizotron), 전기비저항탐사(electrical resistivity tomography), 지표투과레이더(ground penetrating radar, GPR) 등이 널리 사용된다(Alani and Lantini, 2020). 이 중 GPR은 땅속으로 전자파를 방출하고 매질에 의해 반사된 전자파를 수신하여 지하매설물의 분포와 구조를 파악하는 방법이다(Goodman, 1994; Butnor et al., 2001; Zenone et al., 2008). 전자파의 반사 및 회절 특성은 토양조건, 상대유전율, 매질의 형태 및 구조, GPR 사용 주파수 등에 따라 변화하는데(Butnor et al., 2001; Barton and Montagu, 2004; Steinbeck et al., 2022; Almeida Rocha et al., 2024), GPR은 뿌리와 주변 토양의 반사특성 차이를 이용하여 뿌리의 형태적⋅공간적 특성을 탐지할 수 있다. 실례로 Hruska et al.(1999)는 GPR을 이용하여 Quercus petraea 뿌리의 공간적 분포를 조사하였으며, 이후에도 뿌리의 위치와 형태, 지하부 바이오매스 추정 등에 이용된 바 있다(Stover et al., 2007; Alani and Lantini, 2020).
최근에는 GPR을 이용하여 뿌리의 위치와 형태를 보다 정확하게 식별하고 탐지하기 위한 많은 연구가 진행되고 있다(Molon et al., 2017; Aguiar et al., 2021; Almeida Rocha et al., 2024). 뿌리 직경은 GPR로 취득한 반사 신호의 궤적 형태로부터 추정할 수 있다(Butnor et al., 2001; Stover et al., 2007; Yamase et al., 2018). 이 방법은 계산방법이 간단하고 신호 왜곡에 의한 영향을 적게 받지만, 직경을 과대 추정하는 것으로 알려졌다(Yamase et al., 2018; Almeida Rocha et al., 2024). 이를 해결하기 위하여 Aguiar et al.(2021)는 Hilbert 변환이 적용된 반사 신호 궤적에 대해 특정 임계값을 적용하여 뿌리 크기 추정의 정확도를 높혔다. 다만, GPR 신호궤적의 임계값은 토양의 물리적 특성이나 환경조건에 따라 결정되기 때문에 해당 산림에 맞는 임계값 설정이 필요하다.
이 연구는 GPR을 이용하여 수목 뿌리의 공간적 분포를 파악하고 크기를 추정하였으며, GPR 자료가 토양 내 뿌리 보강 효과의 정량적 분석에 활용할 수 있는지 확인하였다. 이를 위해 목재로 제작한 모델뿌리(artifitial tree root)를 이용해 사용주파수에 따른 뿌리의 포착률을 확인하고, GPR로 측정한 뿌리의 위치와 단면의 수직길이를 실측값과 비교하는 실험을 진행하였다. 또한, 단면의 수직길이 추정에 Aguiar et al.(2021)의 방법을 적용하여 GPR 신호를 분석함으로써 임계값에 따른 뿌리 수직길이 추정의 정확도를 평가하고, 이를 토대로 연구대상지에 대한 적정 임계값을 도출하였다.
재료 및 방법
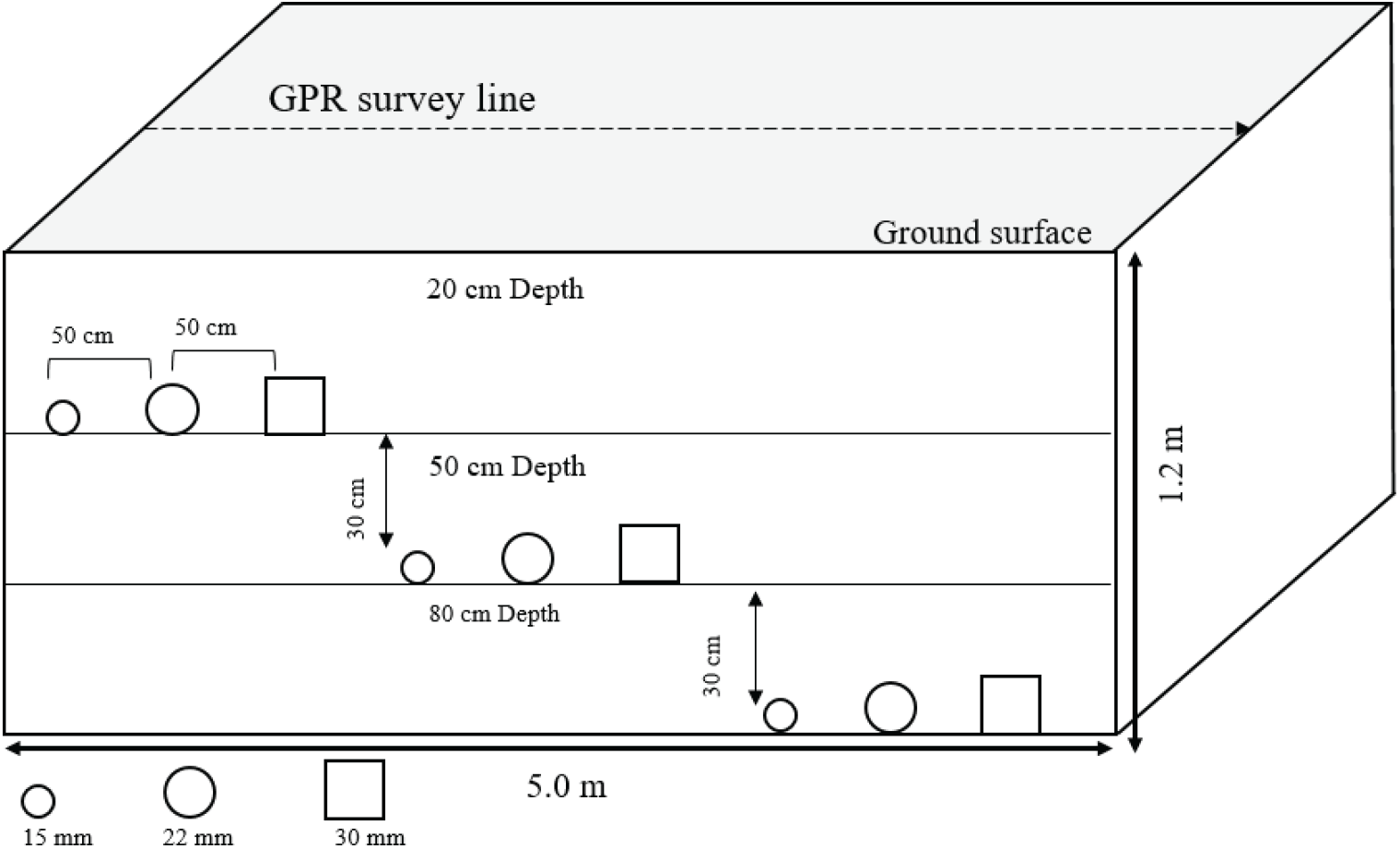
이 연구는 경기도 수원시 권선구 칠보로14번길에 위치한 서울대학교 칠보산 학술림 내 묘포장(37° 15’ 57.45” N, 126° 56’ 20.40” E)에서 수행되었다(Figure 1). 토양 중 암석, 전선, 배수관과 같은 지하매설물은 전자파의 신호 중복이나 신호 감쇠를 일으켜 물체 탐지의 오류를 가져온다. 따라서 이 연구에서는 이러한 매설물이 위치할 가능성이 높은 지역은 실험지 선정에서 제외하였다. 실험지의 토성은 Table 1에 제시된 바와 같이 양토(loamy sand)와 사양토(sandy loam)이다. 실험 당일의 평균기온은 18.8°C였으며, 7일 선행강우량은 9.1 mm로 현장조사 전 5일 동안 강우가 발생하지 않았다. 토양의 용적수분함량은 평균 9.5%로, 토양이 충분히 건조한 것으로 나타났다.

수목 뿌리는 공간적으로 서로 중첩되어 잘 구분되지 않고, 단면 형상이나 크기가 일정하지 않아(Barton and Montagu, 2004; Yamase et al., 2018; Alani and Lantini, 2020) 실제의 뿌리를 이용하여 실험을 진행하는 것에는 한계가 있다. 따라서 이 연구에서는 규격화된 나무 말뚝의 모델뿌리(artificial tree root)를 이용하여 GPR의 뿌리탐지 및 포착능력을 평가하였다. 모델뿌리는 지름이 1.5 cm (C-1.5)와 2.2 cm (C-2.2)의 원형 단면과, 한 변의 길이가 3 cm인 정사각형 단면(R-3)으로 제작하였다. 각 모델뿌리별 길이는 C-1.5와 C-2.2는 40 cm, R-3은 30 cm이며, 각 모델뿌리별로 9개씩 총 27개를 제작하였다.
이 연구에서 사용된 모델뿌리는 Moore and Ryder(2015)가 제안한 방법에 따라 5일 동안 물에 침수시켜 일정 수준의 함수량을 유지하도록 하였다. 이는 함수량 증가가 상대유전율(relative permittivity)을 높이는 주요 요인이기 때문이다(Razafindratsima et al., 2017; Aguiar et al., 2021). 상대유전율은 물질이 전기에너지를 저장하는 능력으로, 물질 내부를 통과하며 전기장이 얼마나 약해지는지를 나타내는 무차원 단위이다(Daniels, 2004; Jol, 2009; Aguiar et al., 2021). 공기의 상대유전율(≈1)에 비해 물의 상대유전율(≈80)이 높기 때문에 함수량이 증가하면 상대유전율도 함께 증가한다(Daniels, 2004; Stover et al., 2007; Razafindratsima et al., 2017; Aguiar et al., 2021). 실험에 사용된 모델뿌리의 침수 후 함수량(gravimetric moisture content)과 용적수분함량(volumetric moisture content)은 각각 평균 56.1%와 25.9%로 나타나, GPR이 식별할 수 있는 뿌리의 최소 수분함량(15%)을 충족하였다(Aboudourib et al., 2019; Aguiar et al., 2021).
GPR에 의한 뿌리 탐지 능력을 평가하기 위해 모델뿌리의 단면형상 및 크기, 모델뿌리의 삽입 깊이, GPR 전자파 주파수를 다르게 설정하여 현장실험을 진행하였다. 실험대상지에 굴삭기를 이용하여 길이 9.5 m, 폭 0.9 m, 깊이 1.2 m의 도랑을 파낸 후, 도랑의 측면에 지면으로부터 0.2 m, 0.5 m, 0.8 m 깊이에서 모델뿌리를 수평으로 삽입하였다. 서로 인접한 물체에서 발생하는 반사파는 2D 이미지에서 중첩되어 외곡된 형태로 나타날 수 있다(Barton and Montagu, 2004). 따라서 인접한 모델뿌리에 의한 신호 중첩을 최소화하고 개별 뿌리를 명확하게 식별하기 위해 50 cm 간격으로 모델뿌리를 삽입하였다. 총 18개의 모델뿌리는 도랑 남쪽 벽면에 50 cm 간격으로 삽입하였고, 나머지 9개 모델뿌리는 반대면에 동일한 간격으로 삽입하였다. GPR 탐지는 뿌리 삽입에 의해 발생하였을지 모르는 토양교란 영향을 최소화하기 위해 삽입 후 2시간 뒤에 조사를 진행하였다.
GPR 기기는 IDS Georadar社의 Operaduo를 사용하였다. Operaduo는 초단파 대역의 250 MHz와 극초단파 대역의 700 MHz 주파수를 사용하는 듀얼 주파수 레이더 시스템이며, 반사된 전자파는 80 ns의 시간 폭(time window)과 512개의 수직 궤적(vertical sample)을 가진다. 사전 조사를 통해 GPR 기기의 전파속도는 0.10 m/ns로 설정하였다. 현장조사는 모델뿌리를 삽입한 지표면 상부에 측선을 설정하고, 측선을 따라 일정한 속도로 GPR 기기를 이동하면서 반사파를 취득하였다. GPR을 이용한 현장조사는 3회 반복하여 실행하였으며, GPR 반사파로부터 형성된 2D 토양단면 이미지를 이용하여 GPR의 모델뿌리 탐지능력(포착률, 뿌리 크기, 삽입깊이)을 평가하였다.
GPR 기기에서 방출된 주파수는 토양 내 대공극, 자갈, 매설물 등 다양한 매질로부터 반사파 왜곡이 발생한다(Stover et al., 2007; Jol, 2009; Aguiar et al., 2021). 이러한 왜곡으로 인해 토양에 존재하는 다른 물체가 뿌리로 오인하여 탐지될 수 있으며(Aguiar et al., 2021), 전처리 과정을 통해 뿌리 탐지에 영향을 미칠 수 있는 전파 왜곡(노이즈)을 제거해야 한다(Stover et al., 2007; Hirano et al., 2009; Jol, 2009).
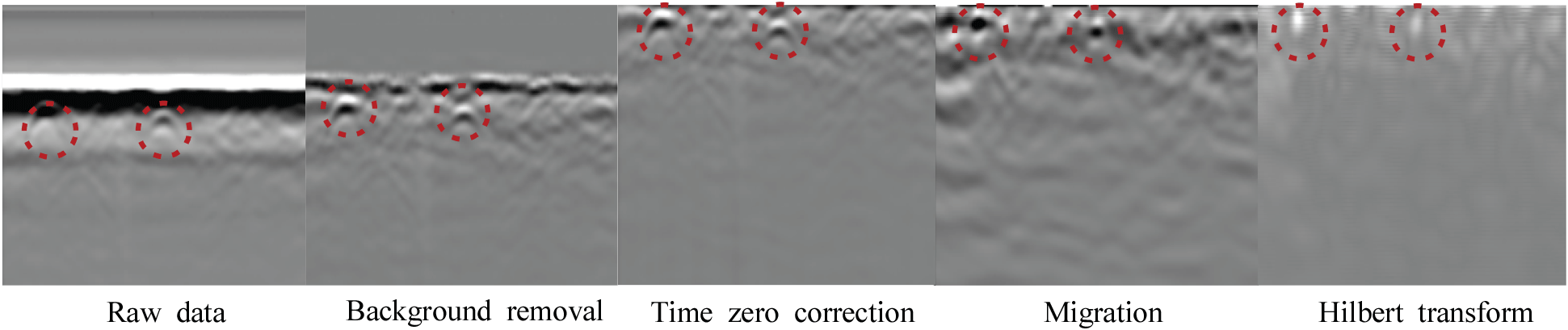
이 연구에서는 IDS Georadar사의 전용 소프트웨어인 GRED HD와 Geophysical Archaeometry Laboratory사의 GPR-slice software (Version 7)를 이용해 현장에서 취득한 GPR 데이터의 전처리를 수행하였다. 전처리 과정은 Figure 6과 같이 background removal, time zero correction, migration, Hilbert 변환(transform) 순으로 진행하였다. 첫 번째 전처리 과정인 background removal은 포물선과 함께 포착된 반사 물질 중 저주파 노이즈(low-frequency noise)를 제거하는 전처리 방법이다(Aguiar et al., 2021). 이 과정을 통하여 원하지 않는 신호를 제거하여 특정 반사 신호의 강도를 높이고자 하였다. 두 번째 전처리 과정인 time zero correction은 GPR에서 최초 전자파 방출 시에 발생하는 시간 지연을 보정하는 기능으로, GPR 기기에서 방출된 전자파가 공기층을 통과할 때 발생하는 시간 지연 오차를 제거하고자 하였다(Jol, 2009; Steinbeck et al., 2022). 세 번째 과정인 migration은 GPR 물체에 반사된 반사파의 실제 위치를 재구성하는 단계로서(Jol, 2009) 주변 매질과 대상물체에 의해 발생하는 전자파 산란 및 회절을 상호 보정하여 정확한 위치 정보를 제공한다(Zhang et al., 2019; Aguiar et al., 2021; Steinbeck et al., 2022). 이 과정을 통해 수목 뿌리의 위치를 보정하여 식별 오류를 감소시키고자 하였다(Lantini et al., 2020). 마지막 전처리 과정인 Hilbert 변환은 전파궤적(trace)의 변화를 계산 및 해석하여 물체를 매질과 명확하게 구분하는 과정이다(Hirano et al., 2009; Aguiar et al., 2021; Almeida Rocha et al., 2024). 이 과정에서는 migration 단계와 더불어 매질에 의해 반사 및 회절된 전자파를 보정하였으며, 이를 통해 특정 전자파 신호를 증폭하여 노이즈와의 구분을 쉽게 하여 신호 해석의 정확성을 높이고자 하였다.
GPR을 이용한 현장조사는 매질과 유전율이 다른 물체에 의해 반사되는 신호 궤적을 이용하여 2D 이미지을 생성한다(Daniels, 2004). 연구자는 취득한 2D 이미지를 통해 지하 물체의 공간적 위치와 크기를 파악할 수 있다(Butnor et al., 2001; Daniels et al., 2004; Ni et al., 2010). 이 연구는 모델뿌리에 대한 GPR 신호궤적의 최대 진폭부터 지표면까지의 시간변화량()에 전파속도를 곱하여 뿌리의 삽입 깊이를 추정하였다. GPR로부터 추정한 모델뿌리의 삽입 깊이는 실제 삽입 깊이와 비교하였다.
물체 크기는 반사파의 최대 진폭지점에서 진폭의 상하 간 시간변화량을 이용하여 추정할 수 있다(Butnor et al., 2001; Yamase et al., 2018; Aguiar et al., 2021; Almeida Rocha et al., 2024). 이를 위하여 모델뿌리 반사 신호궤적 상부와 하부 간의 시간변화량을 구하고, 여기에 GPR 전자파의 전파속도와 곱하여 모델뿌리의 직경을 추정하였다. 이 추정방법은 반사파 2D 이미지로부터 대상물체 형상을 쉽게 검출할 수 있고 매설 깊이에 대한 영향이 비교적 적기 때문에 GPR을 이용한 대상물체 크기 추정에 널리 이용되고 있다(Yamase et al., 2018; Aguiar et al., 2021; Almeida Rocha et al., 2024).
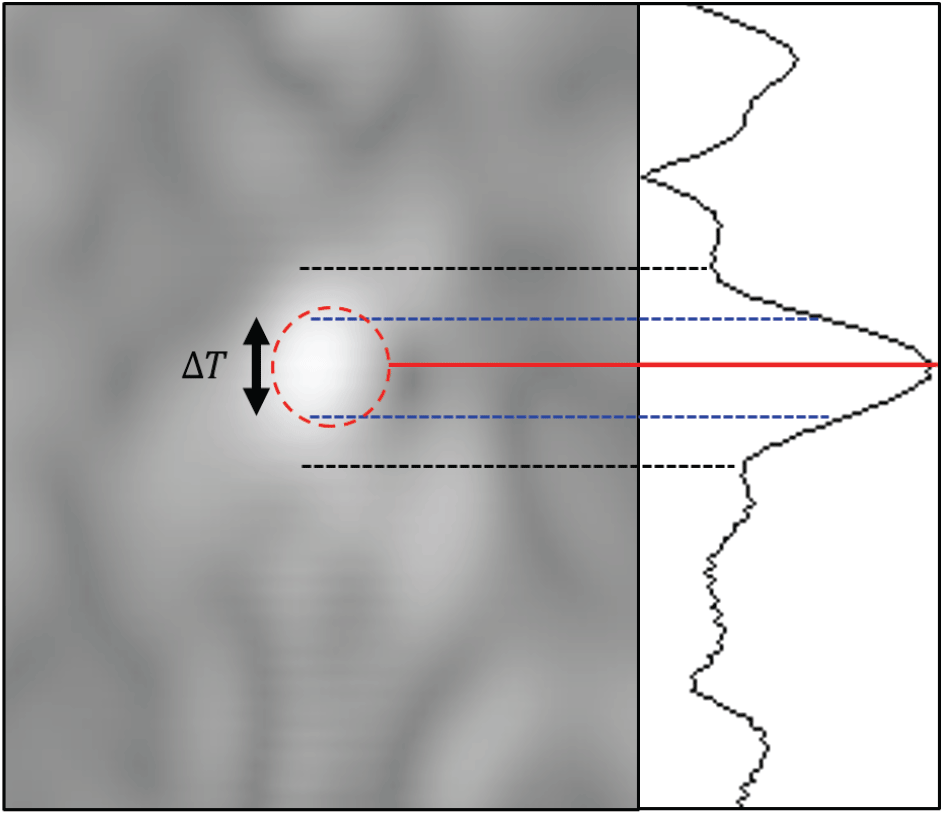
다만, 이러한 방법은 반사파의 시간변화량을 과대하게 추정할 수 있다는 단점이 있다(Aguiar et al., 2021). 시간변화량의 과대 측정은 모델뿌리 삽입 깊이와 크기에 영향을 주기 때문에 과대 추정으로 인한 오차를 줄여야 한다. 이 연구에서는 Aguiar et al.(2021)의 임계값 방법을 적용하였다. 즉, 반사파 궤적의 최대 진폭에 대해 각각 40%, 50%, 60%를 임계값으로 설정하고, 임계값을 넘는 지점의 시간변화량으로부터 모델뿌리의 크기를 추정하였다. Figure 7은 임계값에 따른 시간변화량 변화를 나타내는 그림으로, 붉은 선은 모델뿌리 전파궤적의 최대 진폭 값이며, 검은 점선과 푸른 점선은 각각 40%과 60% 임계값에 해당하는 값을 의미한다. 최종적으로 최대 전파궤적의 임계값에 따라 모델뿌리 개체별 크기를 추정하였으며, 모델뿌리의 실제 크기와 비교하였다.
GPR 자료로 추정한 모델뿌리의 삽입 깊이와 크기를 실측값과 비교하고, 그 결과를 평가하기 위해 평균(Mean), 표준편차(Standard Deviation), 평균절대오차(Mean Absolute Error), 평균제곱근오차(Root Mean Squared Error), 표준오차(Standard Error, SE)를 사용하였다. 평균은 추정값과 실측값 간의 전반적인 경향성을 평가하기 위해 사용하였으며, 평균절대오차는 실제값과 추정값 간의 절대값 오차 평균을 통해 추정값의 정확성을 나타내기 위해 사용하였다. 평균제곱근오차는 평균절대오차에서 반영하기 어려운 큰 오차의 영향을 나타내기 위해 이용하였다. 표준편차는 추정값의 분산 정도를 나타내어 GPR로 추정한 결과의 일관성을 확인하기 위해 활용하였으며, 표준오차는 추정된 평균값의 신뢰성을 평가하기 위해 사용되었다. 이러한 통계적 방법을 통해 GPR로 추정한 자료의 정확성과 신뢰성을 확인하였다. 모든 통계 분석은 R 소프트웨어(R Foundation for Statistical Computiong, Version 3.6.1; http//www.r-project.org)를 이용하였다.
결 과
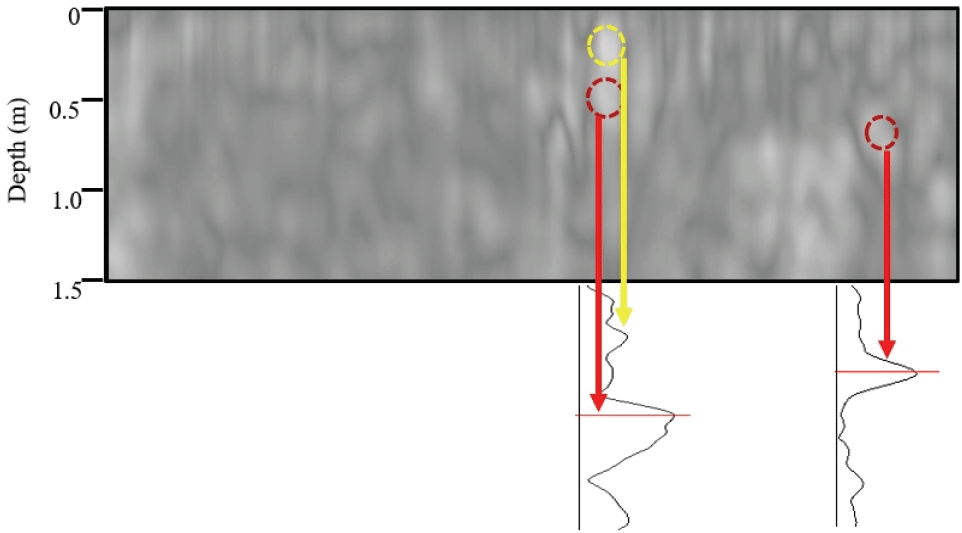
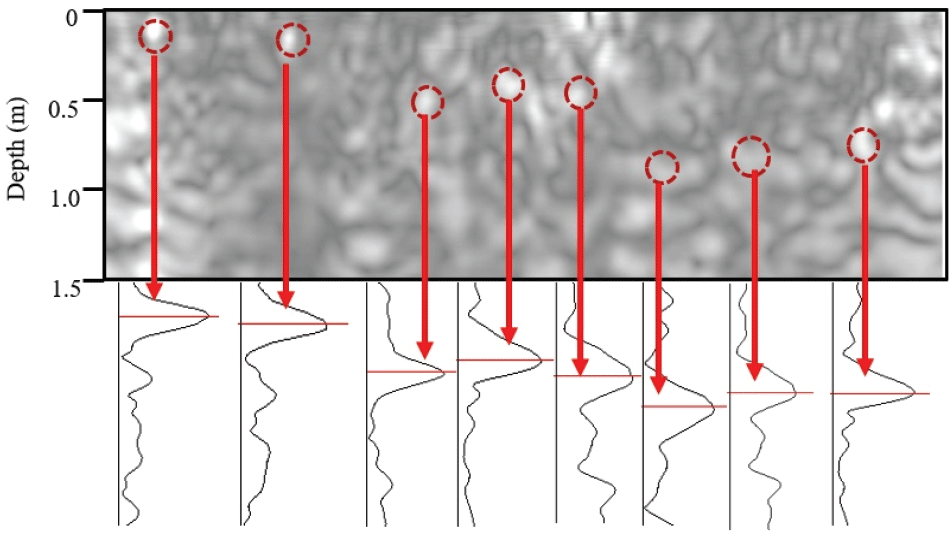
Figure 8과 Figure 9는 GPR 주파수가 각각 250 MHz와 700 MHz일 때 측정한 자료로부터 취득한 토양의 2D 단면 이미지이다. GPR 주파수에 따른 모델뿌리의 포착능력을 확인하기 위해, 각 주파수의 2D 이미지에서 모델뿌리의 포착률을 분석하였다. 그 결과, 250 MHz 주파수보다 700 MHz 주파수의 토양단면 이미지에서 모델뿌리의 포착률이 높았다. 250 MHz 주파수를 사용한 GPR 조사는 낮은 해상도로 인해 12.3%의 모델뿌리 포착률을 보였고, 700 MHz 주파수를 사용한 조사는 86.4%의 포착률로 나타났다. 더불어 원형 단면을 가진 모델뿌리와 정사각형 단면을 가진 모델뿌리의 형태적 차이는 GPR의 2D 이미지에서 명확하게 구분되지 않았다.
Table 2와 Table 3은 각 GPR 주파수의 2D 단면을 이용해 주파수에 따른 모델뿌리의 포착능력을 평가한 결과이다. 이 결과에 따르면, 모델뿌리의 포착률은 삽입 깊이와 단면의 수직길이에 따라 달라졌으며, 250 MHz와 700 MHz 주파수 자료 모두 모델뿌리의 단면 수직길이에 따라 포착률이 달라졌다. 250 MHz 주파수 자료에서 C-1.5 모델뿌리는 0%, C-2.2는 11.1%, R-3는 25.9%의 포착률을 보였으며, 전반적으로 포착률이 낮았다. 반면, 700 MHz 주파수로 모델뿌리를 탐지한 결과, 높은 포착율이 나타났다. C-1.5 모델뿌리 는 66.7%의 포착률을 보였고, C-2.2 는 92.6%, R-3는 100%의 모델뿌리 포착률을 보였다. 두 주파수 모두 모델뿌리의 단면이 커질수록 포착률이 높아지는 결과를 보였기 때문에 GPR의 포착률은 탐지물체의 크기에 비례하여 증가하는 것으로 나타났다.
한편, 모델뿌리의 삽입된 수직 위치가 깊어질수록 GPR에 의한 포착률이 감소하는 경향을 보였다. 이 결과는 두 주파수를 이용해 취득한 토양단면 이미지에서 일관되게 나타났다. GPR의 250 MHz 주파수 취득자료에서는 0.8 m 삽입 깊이에서 7.4%의 모델뿌리 포착률을 보였으며, 0.5 m에서는 11.1%, 0.2 m에서는 18.5%의 포착률을 보였다. 700 MHz 주파수 자료의 모델뿌리 포착률은 0.8 m에서 77.7%, 0.5 m에서 88.9%, 0.2 m에서 92.6%로 나타났다. 따라서, GPR의 물체 포착률은 포착 대상의 지표면으로부터의 깊이에 따라 달라지는 것으로 나타났다.
모델뿌리 포착능력 분석 결과, GPR의 250 MHz 주파수를 이용한 자료는 낮은 모델뿌리 포착률을 보였다. 따라서, 250 MHz 주파수는 모델뿌리 포착에 적합하지 않으며, 700 MHz 이상의 주파수를 이용하는 것이 더 적합하다. 또한 250 MHz 주파수 자료는 낮은 해상도를 보였기 때문에, 추가적인 분석에는 700 MHz 주파수로 취득한 자료만을 이용하였다.
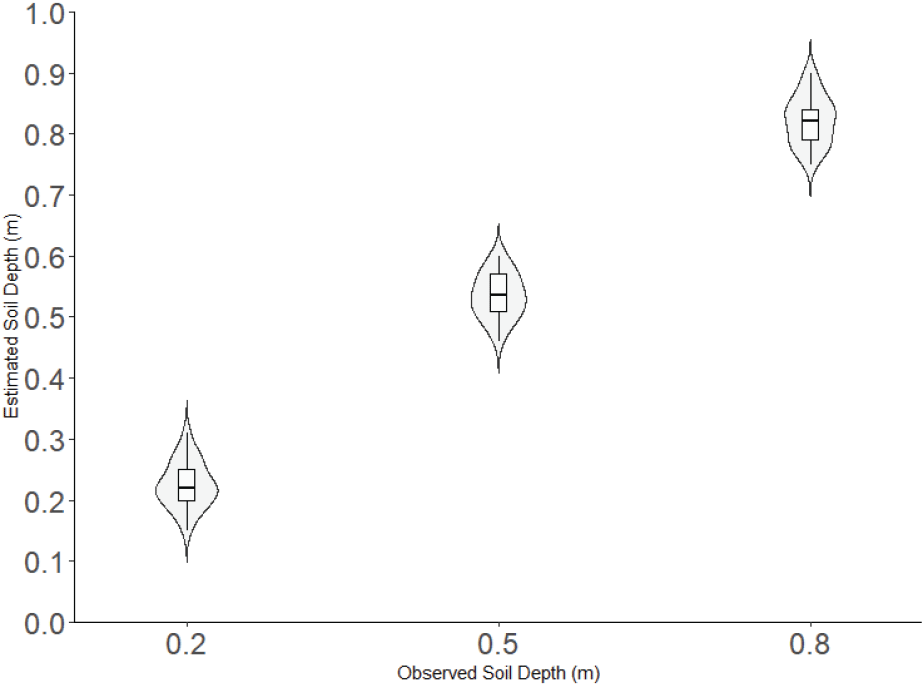
GPR의 700 MHz 주파수 자료를 이용하여 모델뿌리의 삽입 깊이를 추정한 결과는 Table 4와 같다. 지표면으로부터 0.2 m 깊이에 있는 모델뿌리의 추정 깊이는 평균 0.225 m였으며 0.5 m 깊이의 모델뿌리는 0.534 m, 0.8 m는 0.822 m로 추정되었다. 모델뿌리의 삽입위치에 따른 평균절대오차는 실제 삽입 깊이 0.2 m, 0.5 m, 0.8 m에 대해 각각 0.035 m, 0.042 m, 0.037 m로 나타났다. 평균제곱근오차는 각각 0.044 m, 0.050 m, 0.045 m의 오차를 보였다. 표준편차는 0.038 m, 0.037 m, 0.041 m로 나타났으며, 표준 오차는 모두 0.008 m 이하로 나타났다. Figure 10은 GPR에 의해 추정된 모델뿌리의 삽입 위치와 실제 삽입된 위치를 Violin plot과 Box plot으로 나타낸 것으로, GPR은 땅속에 있는 수목 뿌리의 위치를 파악하는 데 적용 가능함을 알 수 있다.
Table 5와 Figure 11은 GPR 반사파의 진폭에 대한 임계값을 고려하여 모델뿌리 단면의 수직길이를 추정한 결과이다. 진폭 임계값이 높을수록 추정 결과는 실측값에 근접해지고 오차율은 감소하였다. 진폭의 임계값으로 40%를 적용한 결과, C-1.5 모델뿌리의 추정 직경의 평균은 2.27 cm이었으며, C-2.2는 2.87 cm로, R-3의 단면 수직길이는 3.72 cm로 추정되었다. 진폭 50% 임계값에서는 모델뿌리 C-1.5, C-2.2, R-3에 대해 단면 길이가 각각 2.11 cm, 2.63 cm, 3.40 cm로 추정되었으며, 60% 임계값을 적용하여 단면을 추정하고 평균한 결과는 각각 1.90 cm, 2.30 cm, 3.06 cm로 나타났다.
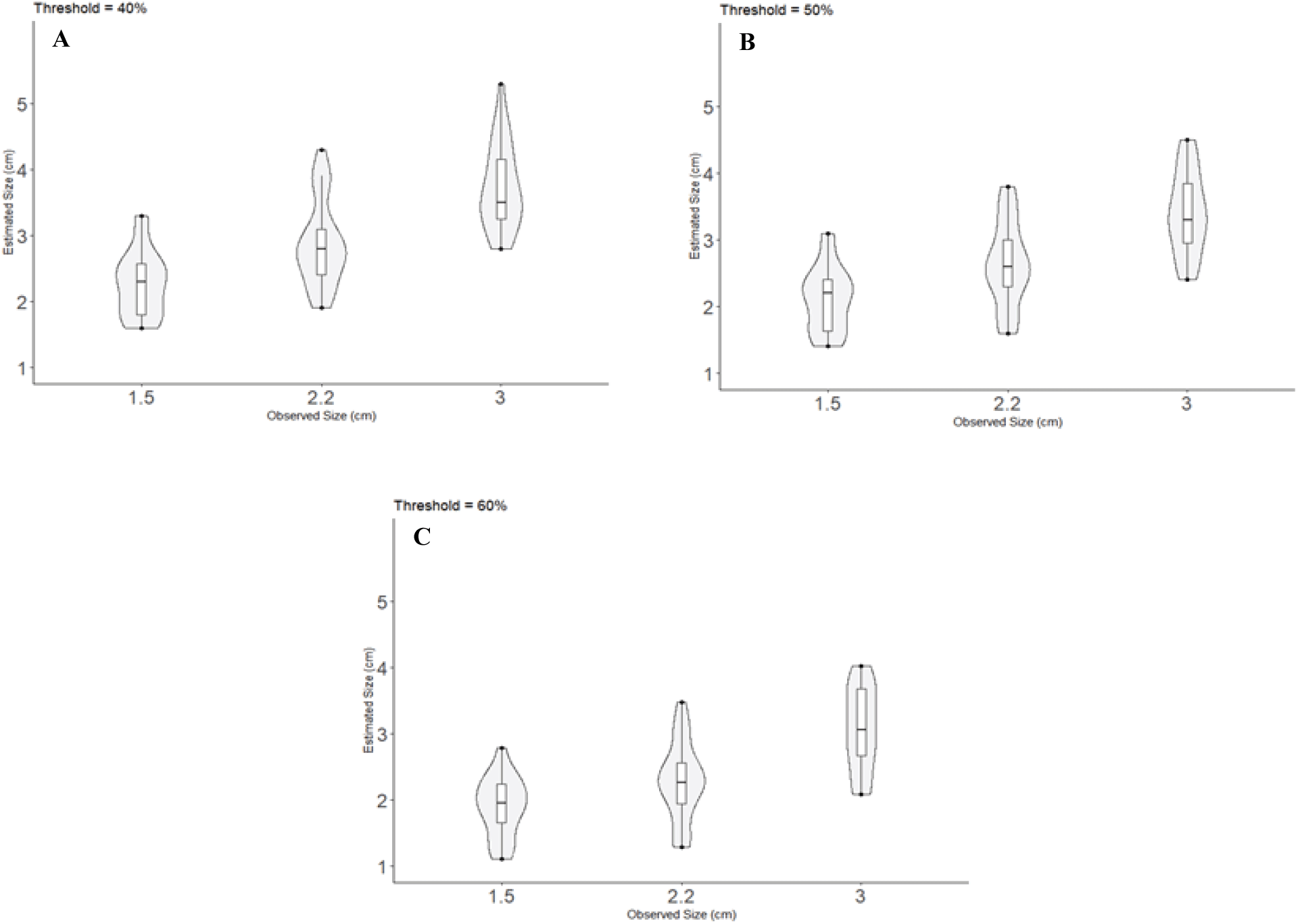
GPR 진폭의 40% 임계값을 적용하여 모델뿌리 단면을 추정한 결과, C-1.5 모델뿌리의 실측값과 추정값 간의 평균절대오차는 0.82 cm이었으며, 모델뿌리 C-2.2와 R-3에 대한 평균절대오차는 0.74 cm과 0.77 cm이었다. 60% 임계값에 대한 크기 추정치의 평균절대오차는 C-1.5, C-2.2, R-3 모델뿌리별로 각각 0.51 cm, 0.44 cm, 및 0.52 cm로 나타났다. 모델뿌리 크기에 대한 추정값과 실측값의 평균절대오차와 평균제곱근오차는 임계값에 비례하여 감소하였다.
모델뿌리의 실제 수직길이와 추정치의 표준편차와 표준오차는 Table 5와 같다. 임계값 40%의 경우, 표준편차는 0.49 cm (C-1.5), 0.64 cm (C-2.2), 0.65 cm (R-3)이었으며, 표준오차는 각각 0.11 cm, 0.13 cm, 0.12 cm로 나타났다. 한편, 60% 임계값에 대해 표준편차가 0.45 cm, 0.58 cm, 0.62 cm로 줄어들었으며, 표준오차는 각각 0.10 cm, 0.11 cm, 0.12 cm로 나타났다.
고 찰
GPR을 이용한 뿌리 포착률은 사용주파수, 해상도, 안테나 방향, 상대유전율, 대상물의 크기 및 공간적 위치 등의 변수에 영향을 받는다(Daniels, 2004; Jol, 2009, Cui et al., 2011; Guo et al., 2013; Guo et al., 2015; Razafindratsima et al., 2017). 이러한 변수들은 상호작용하여 물체의 포착에 영향을 미치며, GPR 사용자는 조사 대상에 적합한 설정을 통해 포착률을 증가시킬 수 있다(Daniels, 2004; Moore and Ryder, 2015; Zhang et al., 2019). 여러 변수 중 GPR의 해상도는 사용주파수와 연관된 변수로, GPR이 물체를 구분하고 식별할 수 있는 능력을 나타낸다(Jol, 2009; Guo et al., 2013). 해상도는 높은 주파수를 사용할수록 증가하며, 해상도가 높을수록 크기가 작은 물질까지 탐지할 수 있다(Butnor et al., 2001; Daniels, 2004; Jol, 2009). 따라서 낮은 해상도의 GPR 이용 시 크기가 작고 조밀한 구성을 가진 물체를 구분하기 어렵다.
Table 2와 Table 3의 결과는 동일한 대상에서 250 MHz 주파수보다 700 MHz 주파수를 사용하였을 때, 더 높은 포착률을 보였음을 나타낸다. 이는 높은 주파수를 사용할수록 작은 물체의 식별과 구분이 원활해진다는 이론적 원칙과 선행연구 결과에 부합한다(Daniels, 2004; Stover et al., 2007; Jol, 2009; Guo et al., 2013). 더불어 Table 2와 Table 3은 GPR 조사 시 물체의 크기가 커질수록, 삽입된 물체가 지표면이랑 가까울수록 포착률이 높아지는 것으로 나타났다. 선행연구 결과에 의하면 700 MHz 주파수의 해상도는 가장 작은 모델뿌리 C-1.5의 탐지에 큰 문제가 없는 것으로 보고되었으나(Hruska et al., 1999; Barton and Montagu 2004; Guo et al., 2013Liu et al., 2019), 이 연구에서는 C-1.5 모델뿌리의 포착률이 다른 모델뿌리보다 낮게 나타났다. 이는 해상도뿐만 아니라 다른 요인들이 탐지 성능에 영향을 미친 것으로 판단된다.
따라서 탐지 성능에 영향을 주는 요인 중 물체의 단면 형태가 미치는 영향을 확인하기 위해, 원형과 정사각형 단면의 모델뿌리를 실험에 이용하였다. 실험 결과 모델뿌리의 단면형태에 따른 신호 패턴의 변화나 2D 토양 단면 이미지에서의 형상 변형이 나타나지 않았다. 특히 모델 뿌리의 반사신호가 단일 반사신호로 나타나 2D 이미지에서 형태적 차이를 확인할 수 없었다. 이를 통해 단면 형태가 GPR의 탐지 능력과 정확도 차이에 미치는 영향이 낮음을 확인하였다. 이러한 결과는 GPR의 반사 신호가 물체의 단면 형태보다 크기와 전자기적 특성에 의해 좌우되기 때문이다(Daniels, 2004; Jol, 2009; Tosti et al., 2018). 따라서 GPR의 특성을 고려하였을 때, 뿌리와 같이 크기가 작은 물체는 단면의 형태가 GPR의 신호에 미치는 영향은 미미한 것으로 판단된다.
이와 같이 물체의 단면 형태가 GPR 탐지 성능에 미치는 영향은 제한적인 반면, 반사강도의 감소는 탐지 성능에 주요한 영향을 미친다(Daniels, 2004; Stover et al., 2007). 이러한 반사강도는 물체의 크기, 위치, 상대유전율에 영향을 받는다(Daniels, 2004; Stover et al., 2007; Molon et al., 2017). C-1.5 모델뿌리는 다른 모델뿌리보다 작은 직경으로 인해 반사되는 신호의 강도가 약하며, 약한 신호강도는 매질을 통과하는 과정에서 발생하는 신호 감쇠와 산란의 영향에 취약하다(Neal, 2004; Guo et al., 2013; Alani and Lantini, 2020). 특히 0.8 m 깊이에 삽입된 C-1.5 모델뿌리는 가장 낮은 포착률을 보였는데, 이는 작은 직경과 토양을 통과하며 발생하는 신호 감쇠 및 산란이 복합적으로 작용하여 물체의 탐지를 더욱 어렵게 만들었음을 나타낸다(Cui et al., 2011).
이러한 문제는 높은 주파수를 사용하면 일부 해결할 수 있지만 높은 주파수의 적용에는 주의가 필요하다(Jol, 2009; Cui et al., 2012). 높은 주파수는 짧은 파장을 이용하여 매질을 투과하며, 짧은 파장은 매질 통과 시 신호의 손실이 빠르게 일어난다(Stover et al., 2007; Jol, 2009). 따라서 높은 주파수는 낮은 투과 깊이를 가진다. GPR 기기 이용자는 조사 대상의 특성과 환경적 요인을 고려하여 주파수를 결정해야 한다(Hruska et al., 1999; Butnor et al., 2001; Stover et al., 2007; Cui et al., 2011). 뿌리는 일반적으로 지표면 아래 1 m 깊이까지 집중되는 것으로 알려져 있으며(Perry, 1982; Jackson et al., 1996; Schenk and Jackson, 2002; Fan et al., 2017), 이를 고려할 때 효과적인 뿌리 조사를 위해서는 700 MHz 에서 1500 MHz 범위의 주파수가 적합한 것으로 판단된다. 이 주파수 범위는 신호의 감쇠를 최소화하며 뿌리의 분포를 파악할 수 있는 투과깊이를 제공할 수 있는 것으로 나타났다(Guo et al., 2013; Liu et al., 2019).
GPR의 물체 포착능력은 매질과 대상물의 상대유전율 차이에도 영향을 받는다(Jol, 2009). 대상과 매질 간의 상대유전율 차이가 클수록 대상물의 탐지가 용이해지는데, 이는 유전율 차이에 따라 반사강도와 진폭이 달라지기 때문이다(Hruska et al., 1999; Butnor et al., 2001; Jol, 2009, Razafindratsima et al., 2017; Alani et al., 2020; Aguiar et al., 2021). 선행 연구에 따르면 나무로 제작된 모델뿌리의 상대 유전상수율은 6-9로 추정되며, 연구대상지의 토양은 4-6 범위로 추정된다(Daniels, 2004; De Jeu et al., 2014; Razafindratsima et al., 2017; Aboudourib et al., 2019). 이 연구에서는 주변 토양 매질과 모델뿌리의 유전율 차이가 크지 않아 뿌리 식별에 영향을 미쳤다. 모델뿌리를 일정 시간 물에 침수시켜 상대유전율을 인위적으로 증가시킴으로써 실제 수목 뿌리와 유사한 반사특성을 갖도록 하였으나, 모델뿌리의 유전율은 Zhang et al.(2019)의 연구에서 밝혀진 뿌리의 실제 유전율보다 낮았으며, 이로 인해 약한 반사강도가 나타나 GPR 탐지 시 포착률이 감소한 것으로 판단된다.
GPR 토양단면 이미지에서 물체의 공간적 위치는 방출된 전자파의 전파속도와 물체에서 반사되어 되돌아오는 시간을 이용해 구한다(Jol, 2009). 이때 반사 물체의 위치는 대상물의 신호궤적에서 진폭이 변화하기 시작하는 시점이나 진폭 변화가 끝난 종점, 또는 최대 진폭 지점을 기준으로 추정한다(Butnor et al., 2001; Molon et al., 2017; Yamase et al., 2018). 그러나 신호궤적의 진폭 변화 시점이나 종점을 기준으로 거리를 구하면 뿌리 위치가 실제보다 과소 혹은 과대하게 산정될 수 있다(Yamase et al., 2018; Almeida Rocha et al., 2024). 이는 GPR 토양단면 이미지에서 물체의 신호궤적을 분석할 때, 진폭 변화가 시작되는 지점과 끝나는 지점을 명확하게 구분하기 어렵기 때문이다(Butnor et al., 2001; Yamase et al., 2018; Aguar et al., 2021). 이 연구에서는 이러한 문제를 해결하기 위하여 신호궤적의 최대 진폭까지의 거리를 뿌리 위치로 해석하였다. 이 연구의 결과인 Table 4에서 모델뿌리 삽입 깊이의 추정값과 실젯값의 차이는 0.025-0.034 m로, 삽입 깊이가 다소 크게 추정되었으나 그 차이는 Moore and Ryder (2015)의 연구결과와 비교하였을 때 작았다. 또한, 세 종류의 모델뿌리 모두 깊이 추정값이 실제보다 크게 나타났으며, 전파속도 조정과 시간 지연 보정을 통해 추가 교정이 가능하다. 이러한 결과는 본 연구에서 사용한 비파괴적 추정 방법이 뿌리의 공간 분포를 정확하게 파악하기에 적합함을 의미한다.
Hilbert 변환은 2D 단면의 생성이나 신호궤적 해석 시에 데이터 가시성을 높여 연구자의 주관적 판단에 따른 오류를 줄여준다(Jol, 2009; Aguiar et al., 2021). 다만, Hilbert 변환과정에서 발생하는 신호궤적 증폭은 물체의 크기를 실제보다 크게 추정될 수 있어 선행연구에서는 임계값을 적용하여 정확성을 높였다(Aguiar et al., 2021; Almeida Rocha et al., 2024). Table 5의 결과는 높은 임계값을 사용할수록 모델뿌리 크기 추정의 정확성이 증가하는 것을 보여준다. 60% 임계값 사용 시 실제 뿌리 크기와 추정치의 오차가 가장 적고, 표준편차와 표준오차도 줄어들어 모델뿌리의 크기를 가장 정확하게 추정하였다. 이러한 결과는 뿌리의 단면길이 추정에 임계값을 적용함으로써, 신호궤적에서 과도한 신호 증폭을 제거하여 뿌리의 실제 반사특성을 정확히 반영한 결과로 판단된다. 뿌리 단면의 정확한 크기 추정은 토양 내 뿌리의 부피와 분포를 보다 정밀하게 평가할 수 있도록 한다(Molon et al., 2017; Yamase et al., 2018; Lantini et al., 2020). 이는 뿌리가 토양에 미치는 보강 효과를 정량적으로 산출하는데 중요한 요소가 된다. 다만, 큰 임계값을 사용하면 모델뿌리의 실제 크기보다 과소 추정되는 경우가 증가하였다. 따라서 적정 임계값의 선정과 적용은 물체의 반사특성과 반사강도를 고려해 결정하여야 한다.
뿌리는 토질역학적 측면에서 토양의 점착력을 높이며 마찰저항을 증가시켜(Genet et al., 2008; Buza and Divós, 2016; Cohen and Schwarz, 2017), 비탈면 안정에 크게 기여한다. 따라서 산지비탈면 안정 해석이나 산사태 예측을 위해서는 뿌리의 토양 보강 효과를 고려하여야 한다(Cohen and Schwarz, 2017; Yamase et al., 2018). 그러나 수목의 뿌리는 산지 환경에 따라 활착이나 크기가 다르고 지하 토양층에 불규칙적으로 분포하기 때문에 직접적인 조사에는 많은 한계가 따른다(Buza and Divós, 2016; Yamase et al., 2018). GPR을 이용한 뿌리 조사는 현장 직접조사에서 발생할 수 있는 한계를 해결하고 뿌리의 직경과 공간적 분포를 정확하게 파악하도록 도와준다. 이 연구에서는 뿌리의 3D 형상 구축보다 뿌리의 2D 이미지 단면에서 직경과 공간적 분포를 정밀하게 추정하고 정확도를 향상시키는데 중점을 두었다. 이러한 정보는 뿌리의 보강효과를 평가하는 모델에서 중요한 인자로 작용하며(Cohen and Schwarz, 2017; Yamase et al., 2018), 이를 바탕으로 토양 내 뿌리의 보강 효과를 정량적으로 분석할 수 있다. 다만, 이 기술이 실제 산림 현장의 뿌리 탐지에 활용되기 위해서는 경사진 산지비탈면에 대한 GPR의 적용성 평가와 GPR 조사로부터 뿌리의 공간적 맵핑(mapping)을 위한 기술개발이 필요하다. 더불어 향후 연구에서는 뿌리의 3D 형상 구축을 통해 뿌리의 전체적인 구조와 분포 특성을 보다 정밀하게 분석하는 연구가 필요하다.
결 론
수목 뿌리는 생장에 필요한 수분과 양분을 흡수하며, 토양을 구조적으로 보강하여 비탈면을 안정화시키고 산사태 발생을 억제한다. GPR은 매질의 전자기파 반사와 회절 특성을 이용하여 뿌리의 형태와 공간적 분포를 탐지하는 비파괴 조사방법으로, 이 연구에서는 목재로 제작한 모델뿌리를 활용하여 뿌리 조사를 위한 GPR의 적용성을 평가하였다.
수목 뿌리의 형태적⋅공간적 특성은 뿌리에 의한 비탈면 안정 해석 및 토양 보강 효과를 정량적으로 파악하는 데 매우 중요하다. 이제까지는 직접 뿌리를 발굴 및 조사하는 방법을 사용해 왔으나, 조사에 필요한 시간 및 비용 문제와 뿌리 훼손으로 인해 대상 수목의 선정 및 조사 개수는 매우 제한적이었다. GPR 비파괴 조사방법은 현장 직접조사의 문제점을 해결할 수 있는 대안이 될 수 있으며, 수목 뿌리의 형태적 특성 및 공간적 분포를 조사하는 데 적용할 수 있다. 이 연구의 결과는 GPR이 현장에서 뿌리의 형태와 공간적 분포를 효과적으로 탐지할 수 있음을 보여준다.
그러나 GPR이 현장에서 활용되기 위해서는 여전히 개선이 필요하다. GPR은 지표면과 수평으로 뻗는 측근 탐지에는 유용하지만, 수직근이나 죽은 뿌리에 대해서는 뿌리 탐지가 제한적이다. 더불어 토양의 수분함량과 뿌리 전자기적 특성에 따라 신호의 변동성이 커질 수 있어, 정확한 뿌리 탐지를 위해서는 추가적인 조정이 필요하다. 향후 수목 뿌리 조사에 GPR을 활용하기 위해서는 반사파 신호처리를 위한 효과적인 전처리 방법과 함께, 뿌리의 공간 분포를 자동 추출하는 매핑기법에 대한 연구도 필요하다.